在C語言中,最大的Reuleaux三角形在一個正方形內
一個盧勒三角形是由三個圓盤的交集形成的形狀,每個圓盤的中心都在其他兩個圓盤的邊界上。它的邊界是一個寬度恆定的曲線,除了圓本身之外,它是最簡單且最知名的這種曲線。寬度恆定意味著每兩條平行支撐線的間隔是相同的,與它們的方向無關。因為它的所有直徑都是相同的。
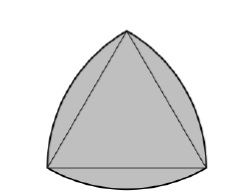
盧勒三角形的邊界是基於等邊三角形的寬度恆定曲線。邊上的所有點與對面的頂點等距離。
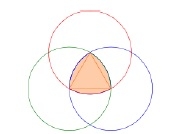
建構一個盧勒三角形
盧勒三角形的公式
如果曲線是基於等邊三角形,三角形的邊長為h ,則盧勒三角形的面積為
A = (π * h<sup>2</sup>) / 2 – 2 * (Area of equilateral triangle) = (π – √3) * h<sup>2</sup> / 2 = 0.70477 * h<sup>2</sup>
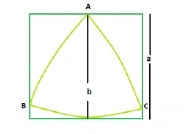
在一個正方形內部找到最大的Reuleaux三角形
#讓我們來舉個例子,
Input: a = 6 Output: 25.3717
說明
魯洛三角形的面積為0.70477 * b2,其中b是平行線之間的距離支援魯洛三角形。
支援魯洛三角形的平行線之間的距離= 正方形的邊長,即a
#魯洛三角形的面積, A = 0.70477 * a2
範例
#include <stdio.h>
#include <math.h>
int main() {
float a = 6;
float area = 0.70477 * pow(a, 2);
printf("The area is : %f",area);
return 0;
}輸出
The area is : 25.371719
以上是在C語言中,最大的Reuleaux三角形在一個正方形內的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

熱門話題
 C語言數據結構:樹和圖的數據表示與操作
Apr 04, 2025 am 11:18 AM
C語言數據結構:樹和圖的數據表示與操作
Apr 04, 2025 am 11:18 AM
C語言數據結構:樹和圖的數據表示與操作樹是一個層次結構的數據結構由節點組成,每個節點包含一個數據元素和指向其子節點的指針二叉樹是一種特殊類型的樹,其中每個節點最多有兩個子節點數據表示structTreeNode{intdata;structTreeNode*left;structTreeNode*right;};操作創建樹遍歷樹(先序、中序、後序)搜索樹插入節點刪除節點圖是一個集合的數據結構,其中的元素是頂點,它們通過邊連接在一起邊可以是帶權或無權的數據表示鄰
 C語言文件操作難題的幕後真相
Apr 04, 2025 am 11:24 AM
C語言文件操作難題的幕後真相
Apr 04, 2025 am 11:24 AM
文件操作難題的真相:文件打開失敗:權限不足、路徑錯誤、文件被佔用。數據寫入失敗:緩衝區已滿、文件不可寫、磁盤空間不足。其他常見問題:文件遍歷緩慢、文本文件編碼不正確、二進製文件讀取錯誤。
 C語言多線程編程:新手指南與疑難解答
Apr 04, 2025 am 10:15 AM
C語言多線程編程:新手指南與疑難解答
Apr 04, 2025 am 10:15 AM
C語言多線程編程指南:創建線程:使用pthread_create()函數,指定線程ID、屬性和線程函數。線程同步:通過互斥鎖、信號量和條件變量防止數據競爭。實戰案例:使用多線程計算斐波那契數,將任務分配給多個線程並同步結果。疑難解答:解決程序崩潰、線程停止響應和性能瓶頸等問題。
 CS-第 3 週
Apr 04, 2025 am 06:06 AM
CS-第 3 週
Apr 04, 2025 am 06:06 AM
算法是解決問題的指令集,其執行速度和內存佔用各不相同。編程中,許多算法都基於數據搜索和排序。本文將介紹幾種數據檢索和排序算法。線性搜索假設有一個數組[20,500,10,5,100,1,50],需要查找數字50。線性搜索算法會逐個檢查數組中的每個元素,直到找到目標值或遍歷完整個數組。算法流程圖如下:線性搜索的偽代碼如下:檢查每個元素:如果找到目標值:返回true返回falseC語言實現:#include#includeintmain(void){i
 c語言如何輸出倒數
Apr 04, 2025 am 08:54 AM
c語言如何輸出倒數
Apr 04, 2025 am 08:54 AM
如何在 C 語言中輸出倒數?回答:使用循環語句。步驟:1. 定義變量 n 存儲要輸出的倒數數字;2. 使用 while 循環持續打印 n 直到 n 小於 1;3. 在循環體內,打印出 n 的值;4. 在循環末尾,將 n 減去 1 以輸出下一個更小的倒數。
 C語言數據結構:數據結構在人工智能中的關鍵作用
Apr 04, 2025 am 10:45 AM
C語言數據結構:數據結構在人工智能中的關鍵作用
Apr 04, 2025 am 10:45 AM
C語言數據結構:數據結構在人工智能中的關鍵作用概述在人工智能領域,數據結構對於處理大量數據至關重要。數據結構提供了一種組織和管理數據的有效方法,優化算法和提高程序的效率。常見的數據結構C語言中常用的數據結構包括:數組:一組連續存儲的數據項,具有相同的類型。結構體:將不同類型的數據組織在一起並賦予它們一個名稱的數據類型。鍊錶:一種線性數據結構,其中數據項通過指針連接在一起。堆棧:遵循後進先出(LIFO)原理的數據結構。隊列:遵循先進先出(FIFO)原理的數據結構。實戰案例:圖論中的鄰接表在人工智
 c語言函數的概念及其定義格式
Apr 03, 2025 pm 11:33 PM
c語言函數的概念及其定義格式
Apr 03, 2025 pm 11:33 PM
C语言函数是可重复使用的代码块,接收参数进行处理,返回结果。它类似于瑞士军刀,功能强大,需要谨慎使用。函数包括定义格式、参数、返回值、函数体等元素。高级用法包括函数指针,递归函数和回调函数。常见错误是类型不匹配、忘记声明原型。调试技巧包括打印变量、使用调试器。性能优化使用内联函数。函数设计应遵循单一职责原则。熟练掌握C语言函数可以显著提高编程效率和代码质量。
 C語言處理文件時的疑難解答錦囊
Apr 04, 2025 am 11:15 AM
C語言處理文件時的疑難解答錦囊
Apr 04, 2025 am 11:15 AM
C語言處理文件時的疑難解答錦囊在C語言中處理文件時,可能會遇到各種問題,以下是常見問題及對應的解決方法:問題1:無法打開文件代碼:FILE*fp=fopen("myfile.txt","r");if(fp==NULL){//文件打開失敗}原因:文件路徑錯誤文件不存在沒有文件的讀取權限解決方法:檢查文件路徑確保文件存在檢查文件權限問題2:文件讀取失敗代碼:charbuffer[100];size_tread_bytes=fread(buffer,1,siz






