檢查給定的圖中兩個節點之間的路徑是否表示最短路徑

要檢查圖表的兩個中心之間的給定路徑是否符合最短路徑,可以透過使用可靠的最短路徑將沿著給定路徑的整個邊緣權重與相同中心組合之間的最短距離進行比較方式計算,例如Dijkstra 計算或Floyd−Warshall 計算。如果給定路徑上的所有邊權重與最有限的刪除相匹配,那麼它就代表最簡單的路徑。另外:如果整個邊權重比最短距離更突出,則表示圖表中兩個中心之間存在較短的距離。
使用的方法
Dijkstra 演算法
具有邊緣反轉成本的 Floyd−Warshall 演算法
貪心演算法
Dijkstra 的計算可能是一種流行的圖表遍歷計算,用於發現圖表中來源中心與所有其他中心之間最有限的路徑。在檢查兩個中心之間的給定路徑是否與最有限路徑相關的情況下,Dijkstra 的計算可用於計算這些中心之間的最有限間隔。透過從起始樞紐運行 Dijkstra 的計算,我們得到所有其他樞紐的最有限的間隔。如果給定的路線與兩個樞紐之間的最有限距離相匹配,那麼它就表示一條實質性且最短的路線。其他:如果給定的路線比計算的最短距離長,則表示圖表中存在較短的路線。
演算法
建立最短路徑(圖形、來源、目的地):
#初始化一組「過去」來儲存去往中心的距離,並初始化一個單字參考間隔來儲存最有限的距離。
在分隔字典中將來源集線器的間隔設為無限,並將所有其他中心的間隔設為無限。
雖然存在未存取的節點,
a。選擇與分隔詞參考距離最小的中心並將其標記為已訪問。
b。對於目前節點的每個鄰居集線器:
#透過將邊權重加到目前節點的距離來計算臨時間隔。
如果條件間距小於存放間距,則檢修距離。
如果在分離中從來源到目標的最短距離與給定路徑長度收支平衡,則傳回 true(給定路徑表示最短路徑)。其他情況,傳回 false。
此計算利用 Dijkstra 方法來計算最短間隔,然後將從來源到目標的最短距離與給定的路徑長度進行比較,以確定是否為最短的路徑.
#範例
#include <iostream>
#include <vector>
#include <queue>
#include <limits>
using namespace std;
const int INF = numeric_limits<int>::max();
bool shortestPath(vector<vector<pair<int, int>>>& graph, int source, int destination, int pathLength) {
int numNodes = graph.size();
vector<int> distances(numNodes, INF);
distances[source] = 0;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.emplace(0, source);
while (!pq.empty()) {
int u = pq.top().second;
int dist = pq.top().first;
pq.pop();
if (dist > distances[u])
continue;
for (auto& neighbor : graph[u]) {
int v = neighbor.first;
int weight = neighbor.second;
if (dist + weight < distances[v]) {
distances[v] = dist + weight;
pq.emplace(distances[v], v);
}
}
}
return (distances[destination] == pathLength);
}
int main() {
int numNodes = 6;
vector<vector<pair<int, int>>> graph(numNodes);
// Build the graph
graph[0].emplace_back(1, 2);
graph[0].emplace_back(2, 5);
graph[1].emplace_back(3, 4);
graph[1].emplace_back(4, 1);
graph[2].emplace_back(3, 2);
graph[3].emplace_back(4, 3);
graph[3].emplace_back(5, 6);
graph[4].emplace_back(5, 2);
int source = 0;
int destination = 5;
int pathLength = 8;
bool isShortestPath = shortestPath(graph, source, destination, pathLength);
if (isShortestPath)
cout << "The given path represents a shortest path." << endl;
else
cout << "The given path does not represent a shortest path." << endl;
return 0;
}
輸出
The given path does not represent a shortest path.
具有邊緣反轉成本的 Floyd−Warshall 演算法
Floyd-Warshall 計算是一種動態程式計算,用於發現圖表中所有中心對之間的最短路徑。在檢查兩個中心之間的給定路徑是否與最有限路徑相關的情況下,Floyd-Warshall 計算可用於計算圖表中所有中心集之間的最短間隔。透過將計算得到的最短距離與給定路徑上的全部邊權重進行比較,我們就可以確定給定路徑是否涉及最有限的路徑。如果整個邊權重與最短的間隔相匹配,則此時給定的路徑可能是圖表中兩個中心之間最有限的路徑。演算法
製作一個測量 numNodes x numNodes 的二維格子,並為所有節點集將其初始化為無限 (INF)。
將 dist 的角對角加法設定為 0。
對於圖表中權重為w 的每個協調邊(u, v),將dist[u][v] 徹底修改為w,將dist[v][u] 修改為w w_reversal,其中w_reversal 是反轉透過邊(v,u)的方式取得。
在固定迴圈後執行 Floyd−Warshall 計算:
對於從 numNodes 到 1 之間的每個中途集線器,請執行以下操作:
對於從 numNodes 到 1 的集線器 i 和 j 的每個聚合,將 dist[i][j] 改進到以下值中的最小值:
距離[i][j]
距離[i][k]距離[k][j]
計算完成後,考慮到邊緣反轉成本,dist 將包含所有集線器組之間最有限的間隔。
要檢查兩個樞紐(來源和目標)之間的給定路線是否為最簡短的路線,請將給定路線的長度與距離 [來源] [目的地] 進行比較。如果是的話,給定的方式是最有限的方式。
範例
#include <iostream>
#include <vector>
using namespace std;
const int INF = 1e9;
void floydWarshall(vector<vector<int>>& graph, int numNodes) {
vector<vector<int>> dist(graph); // Distance matrix initialized with the graph
for (int k = 0; k < numNodes; k++) {
for (int i = 0; i < numNodes; i++) {
for (int j = 0; j < numNodes; j++) {
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
// Printing the shortest distances
cout << "Shortest distances between all pairs of nodes:" << endl;
for (int i = 0; i < numNodes; i++) {
for (int j = 0; j < numNodes; j++) {
if (dist[i][j] == INF)
cout << "INF ";
else
cout << dist[i][j] << " ";
}
cout << endl;
}
}
int main() {
int numNodes = 4; // Number of nodes
// Adjacency matrix representation of the graph with edge weights and edge reversal costs
vector<vector<int>> graph = {
{0, 5, INF, 10},
{INF, 0, 3, INF},
{INF, INF, 0, 1},
{INF, INF, INF, 0}
};
floydWarshall(graph, numNodes);
return 0;
}
輸出
Shortest distances between all pairs of nodes: 0 5 8 9 INF 0 3 4 INF INF 0 1 INF INF INF 0
結論
本文探討如何檢查圖表的兩個中心之間的給定路徑是否代表最有限的路徑。它闡明了兩種方法:Dijkstra 計算和獲取邊緣反轉的 Floyd-Warshall 計算。 C 中的程式碼用法說明了這些計算。它還簡要說明了計算及其用途。本文旨在幫助讀者了解如何在圖表中找到最有限的方法,並確定給定的方法是否無疑是最簡單的。
以上是檢查給定的圖中兩個節點之間的路徑是否表示最短路徑的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
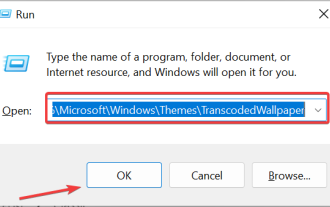 主題背景位於 Windows 11 中的什麼位置?
Aug 01, 2023 am 09:29 AM
主題背景位於 Windows 11 中的什麼位置?
Aug 01, 2023 am 09:29 AM
Windows11具有如此多的自訂選項,包括一系列主題和桌布。雖然這些主題以自己的方式是美學,但有些用戶仍然想知道他們在Windows11上的後台位置。本指南將展示造訪Windows11主題背景位置的不同方法。什麼是Windows11預設主題背景? Windows11預設主題背景是一朵盛開的抽象寶藍色花朵,背景為天藍色。這種背景是最受歡迎的背景之一,這要歸功於作業系統發布之前的預期。但是,作業系統還附帶了一系列其他背景。因此,您可以隨時變更Windows11桌面主題背景。主題背景儲存在Windo
 斜線和反斜線在檔案路徑中的不同使用
Feb 26, 2024 pm 04:36 PM
斜線和反斜線在檔案路徑中的不同使用
Feb 26, 2024 pm 04:36 PM
檔案路徑是作業系統中用於識別和定位檔案或資料夾的字串。在檔案路徑中,常見的有兩種符號分隔路徑,即正斜線(/)和反斜線()。這兩個符號在不同的作業系統中有不同的使用方式和意義。正斜線(/)是Unix和Linux系統中常用的路徑分隔符號。在這些系統中,檔案路徑是以根目錄(/)為起始點,每個目錄之間使用正斜線進行分隔。例如,路徑/home/user/Docume
 如何修復錯誤:在Java中找不到或載入主類
Oct 26, 2023 pm 11:17 PM
如何修復錯誤:在Java中找不到或載入主類
Oct 26, 2023 pm 11:17 PM
由於技術錯誤,無法播放此影片。 (錯誤代碼:102006)本指南提供了針對此常見問題的簡單修復,並繼續您的編碼之旅。我們還將討論Java錯誤的原因以及將來如何防止它。什麼是Java中的「錯誤:找不到或載入主類別」? Java是一種強大的程式語言,使開發人員能夠創建廣泛的應用程式。然而,它的多功能性和效率伴隨著開發過程中可能發生的一系列常見錯誤。其中一個中斷是錯誤:找不到或載入主類別user_jvm_args.txt,當Java虛擬機器(JVM)找不到主類別來執行程式時會出現這種情況。此錯誤充當了障礙,甚至在
 如何使用C++中的Prim演算法
Sep 20, 2023 pm 12:31 PM
如何使用C++中的Prim演算法
Sep 20, 2023 pm 12:31 PM
標題:C++中Prim演算法的使用及程式碼範例引言:Prim演算法是一種常用的最小生成樹演算法,主要用於解決圖論中的最小生成樹問題。在C++中,透過合理的資料結構和演算法實現,可以有效地使用Prim演算法。本文將介紹如何在C++中使用Prim演算法,並提供具體的程式碼範例。一、Prim演算法簡介Prim演算法是一種貪心演算法,它從一個頂點開始,逐步擴展最小生成樹的頂點集合,直到套件
 Win11系統中「我的電腦」路徑有何不同?快速找方法!
Mar 29, 2024 pm 12:33 PM
Win11系統中「我的電腦」路徑有何不同?快速找方法!
Mar 29, 2024 pm 12:33 PM
Win11系統中「我的電腦」路徑有何不同?快速找方法!隨著Windows系統的不斷更新,最新的Windows11系統也帶來了一些新的變化和功能。其中一個常見的問題是使用者在Win11系統中找不到「我的電腦」的路徑,這在先前的Windows系統中通常是很簡單的操作。本文將介紹Win11系統中「我的電腦」的路徑有何不同,以及快速尋找的方法。在Windows1
 使用path/filepath.Dir函數取得檔案路徑的目錄部分
Jul 27, 2023 am 09:06 AM
使用path/filepath.Dir函數取得檔案路徑的目錄部分
Jul 27, 2023 am 09:06 AM
使用path/filepath.Dir函數取得檔案路徑的目錄部分在我們的日常開發過程中,經常會涉及到檔案路徑的處理。有時候,我們需要取得檔案路徑的目錄部分,也就是檔案所在資料夾的路徑。在Go語言中,可以使用path/filepath套件提供的Dir函數來實現這個功能。 Dir函數的簽章如下:funcDir(pathstring)stringDir函式接收一個字
 如何查找Linux系統中RPM檔案的儲存路徑?
Mar 14, 2024 pm 04:42 PM
如何查找Linux系統中RPM檔案的儲存路徑?
Mar 14, 2024 pm 04:42 PM
在Linux系統中,RPM(RedHatPackageManager)是一種常見的軟體套件管理工具,用於安裝、升級和移除軟體套件。有時候我們需要找到某個已安裝的RPM檔案的儲存路徑,以便進行尋找或其他操作。以下將介紹在Linux系統中如何找到RPM檔案的儲存路徑,同時提供具體的程式碼範例。首先,我們可以使用rpm指令來尋找已安裝的RPM套件及其儲存路徑。打開
 Linux核心原始碼存放路徑解析
Mar 14, 2024 am 11:45 AM
Linux核心原始碼存放路徑解析
Mar 14, 2024 am 11:45 AM
Linux內核是一個開源的作業系統內核,其原始碼儲存在一個專門的程式碼倉庫中。在本文中,我們將詳細解析Linux核心原始碼的存放路徑,並透過具體的程式碼範例來幫助讀者更好地理解。 1.Linux核心原始碼存放路徑Linux核心原始碼儲存在一個名為linux的Git倉庫中,該倉庫託管在[https://github.com/torvalds/linux](http






