給定一個非循環圖，計算每個深度的最小元素總和

不包含任何循環或迴路的圖稱為非循環圖。樹是一種非循環圖，其中每個節點都與另一個唯一節點相連。非循環圖也稱為無環圖。

循環圖與非循環圖的差異 -

的中文翻譯為：

Cycle Graph	循環圖	非循環圖
#圖形形成一個閉環。	圖表沒有形成閉環。
圖表中不包含深度循環	圖表包含每個深度。

範例 1

讓我們舉一個循環圖的例子 −

當閉環存在時，就形成了循環圖。

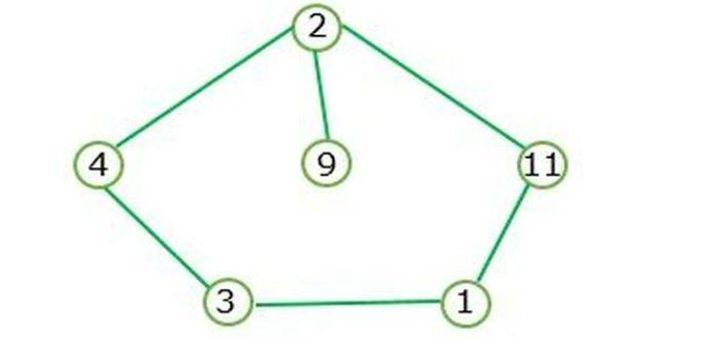
Figure I代表了循環圖，不包含深度節點。

Example 2

的翻譯為：

範例2

讓我們以一個非循環圖的例子來說明：

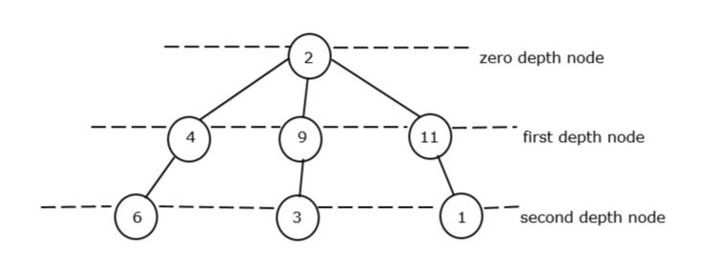
樹的根節點稱為零深度節點。在圖 II 中，在零深度處只有一個根，即 2。因此它被認為是最小深度為零的節點。

在第一個深度節點中，我們有3個節點元素，如4、9和1，但最小的元素是4。

在第二個深度節點中，我們又有3個節點元素，如6、3和1，但最小元素是1。

我們將知道總深度節點是如何得出的，

總深度節點 = Zero_Depth 節點的最小值 First_Depth 節點的最小值 Zero_Depth 節點的最小值

總深度節點 = 2 4 3 = 9。所以，9是非循環圖的總最小和。

文法

The following syntax used in the program:
struct name_of_structure{
   data_type var_name;   
   // data member or field of the structure.
}

• struct − 此關鍵字用來表示結構資料型態。

• name_of_struct - 我們為結構提供任何名稱。

• 結構是將各種相關變數集中在一個地方的集合。

Queue < pair < datatype, datatype> > queue_of_pair

make_pair() 

參數

C 中的對隊列 -

• 這是用於組合兩種不同資料類型的佇列對的通用 STL 模板，佇列對位於公用程式頭檔下。

• Queue_of_pair - 我們為該對指定任何名稱。

• make_pair() - 用於建構具有兩個元素的pair物件。

name_of_queue.push()

參數

• name_of_queue - 我們正在命名佇列名稱。

• push() − 這是一個預先定義的方法，屬於佇列頭部的一部分，push方法的作用是插入元素或值。

name_of_queue.pop()

參數

• name_of_queue − 我們正在為佇列命名。

• pop() − 這是一個預先定義的方法，屬於佇列頭文件，並且使用pop方法是為了刪除整個元素或值。

演算法

• 我們將啟動程式頭文件，即'iostream'、'climits'、'utility'、和'queue'。

  < /里>

• #我們正在建立具有整數值「val」的結構「tree_node」來取得節點值。然後我們用給定的資料建立tree_node指標來初始化左子節點和右子節點來儲存值。接下來，我們建立一個 tree_node 函數，其中 int x 作為參數傳遞，並驗證它是否等於 'val' 整數，並將左右子節點指派為 null 。

• 現在我們將定義一個函數 minimum_sum_at_each_depth()，它接受一個整數值作為參數，用於找到每個深度的最小和。使用 if- 語句，它檢查樹的根值是否為空，如果為空則傳回 0。

• 我們正在建立STL（標準範本庫）的佇列對，以組合兩個值。

• 我們建立了一個名為q的佇列變量，它會作為一對進行兩個方法，即push()和make_pair()。使用這兩個方法，我們插入值並建構了一個物件的兩對。

• 我們正在初始化三個變量，即 'present_depth'，'present_sum' 和 'totalSum'，這些變數將用於進一步找到當前總和以及找到總最小總和。

• 在初始化變數之後，我們建立一個while迴圈來檢查條件，如果佇列對不為空，則節點的計數將從開頭開始。接下來，我們使用‘pop()’方法刪除一個現有的節點，因為它將移動到樹的下一個深度來計算最小和。

• 現在我們將建立三個 if 語句來傳回總和的最小和。

• 在此之後，我們將開始主要的函數，並藉助根指標、左右子節點分別建立輸入模式的樹狀結構，並透過新的'tree_node'傳遞節點值。

• 最後，我們呼叫‘minimum_sum_at_each_depth(root)’函數並傳遞參數root來計算每個深度的最小總和。接下來，列印語句「非循環圖各深度的總和」並得到結果。

請記住，對佇列是一個包含佇列元素對的容器。

Example

的中文翻譯為：

範例

在這個程式中，我們將計算每個深度的所有最小節點的總和。

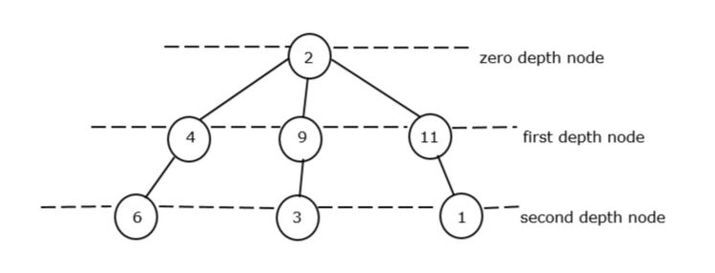
在圖二中，總深度的最小和為15 8 4 1 = 13。

现在我们将把这个数字作为该程序的输入。

#include <iostream>
#include <queue> 

// required for FIFO operation
#include <utility> 

// required for queue pair
#include <climits>
using namespace std;

// create the structure definition for a binary tree node of non-cycle graph
struct tree_node {
   int val;
   tree_node *left;
   tree_node *right;
   tree_node(int x) {
      val = x;
      left = NULL;
      right = NULL;
   }
};
// This function is used to find the minimum sum at each depth
int minimum_sum_at_each_depth(tree_node* root) {
   if (root == NULL) {
      return 0;
   }
   queue<pair<tree_node*, int>> q;
   // create a queue to store node and depth and include pair to combine two together values.
   q.push(make_pair(root, 0)); 
   
   // construct a pair object with two element
   int present_depth = -1; 
   
   // present depth
   int present_sum = 0; 
   
   // present sum for present depth
   int totalSum = 0; 
   
   // Total sum for all depths
   while (!q.empty()) {
      pair<tree_node*, int> present = q.front(); 
      
      // assign queue pair - present
      q.pop();
      
      // delete an existing element from the beginning
      if (present.second != present_depth) {
      
         // We are moving to a new depth, so update the total sum and reset the present sum
         present_depth = present.second;
         totalSum += present_sum;
         present_sum = INT_MAX;
      }

      // Update the present sum with the value of the present node
      present_sum = min(present_sum, present.first->val);
      
      //We are adding left and right children to the queue for updating the new depth.
      if (present.first->left) {
         q.push(make_pair(present.first->left, present.second + 1));
      }
      if (present.first->right) {
         q.push(make_pair(present.first->right, present.second + 1));
      }
   }
   
   // We are adding the present sum of last depth to the total sum
   totalSum += present_sum;
   return totalSum;
}

// start the main function
int main() {
   tree_node *root = new tree_node(15);
   root->left = new tree_node(14);
   root->left->left = new tree_node(11);
   root->left->right = new tree_node(4);
   root->right = new tree_node(8);
   root->right->left = new tree_node(13);
   root->right->right = new tree_node(16);
   root->left->left->left = new tree_node(1);
   root->left->right->left = new tree_node(6);
   root->right->right->right = new tree_node(2);
   root->right->left->right = new tree_node(7);

   cout << "Total sum at each depth of non cycle graph: " << minimum_sum_at_each_depth(root) << endl; 
   return 0;
}

输出

Total sum at each depth of non cycle graph: 28

结论

我们探讨了给定非循环图中每个深度的元素最小和的概念。我们看到箭头运算符连接节点并构建树形结构，利用它计算每个深度的最小和。该应用程序使用非循环图，例如城市规划、网络拓扑、谷歌地图等。

以上是給定一個非循環圖，計算每個深度的最小元素總和的詳細內容。更多資訊請關注PHP中文網其他相關文章！