在一個範圍內評估給定方程式的查詢

對區間 [L, R] 內的所有方程式進行評估,為我們提供了這些變數的一系列值。如何使用它的範例包括建模、資料分析和解決問題的場景。
在這種情況下,我們為範圍內的所有點定義方程式變數值。因此,可以透過指定範圍的步長並評估範圍內每個變數值的方程式來完成。
規格
這可以稱為向資料庫詢問資訊的請求。當滿足某些要求時,使用特定命令提取資料。為了從資料庫中取得、過濾、排序和匯總數據,查詢經常用程式語言編寫。查詢可以很簡單,具體取決於必須提取的資料和資訊的複雜性。
接受方程式範圍 [L, R] 和步長作為輸入並為範圍內變數的每個值產生方程式結果的電腦程式可用於自動執行此過程。
問題處理方法
在一定範圍內尋找給定方程式的值是評估範圍 [L, R] 內任何給定方程式的查詢的目標。這是用於類似查詢的潛在方法 -
解析提供的方程式並從中建立表達式樹。二元樹可用於視覺化表達式樹,每個節點代表方程式中的運算子或運算元。
對表達式樹進行預先排序並迭代每個子樹,評估每個子樹的方程式。表達式樹的每個節點都應包含結果。
建立範圍查詢函數,接受表達式樹的根、下界 L 和上限 R 作為輸入。此函數的目標是迭代表達式樹並傳回所提供的 [L, R] 範圍的方程式解。
可以額外預先計算並保存指定範圍[L,R]的每個子範圍的方程式解,以改善範圍查詢功能。
最後,我們可以使用範圍查詢函數計算不同範圍的方程式。
文法
在 C 中,可以使用循環來迭代每個範圍中的值,然後將提供的方程式應用於每個值以確定其在 [L, R] 範圍內的評估。對於 [L, R] 範圍內的每個 x 值,建立以下循環來評估方程式 -
y = x2 + 2x + 1
// Define equation to evaluate
int equation(int x) {
return x*x + 2*x + 1;
}
// Evaluate equation for every value of x in range [L, R]
int L, R; // Define the range
for (int x = L; x <= R; x++) {
int y = equation(x);
// Do something with value of y like print it
cout << "x = " << x << ", y = " << y << endl;
}
演算法
這是評估區間 [L, R] 中的方程式的 C 演算法 -
步驟 1 - 舉例說明如何將方程式定義為接收變數 x 並傳回值 y 的函數 -
步驟 2 - 寫函數,接受兩個整數 L 和 R 作為參數,並輸出 L 和 R 之間每個整數值的方程式解。可以使用循環遍歷範圍 [L, R],評估每個整數值的方程式 -
步驟3 - 在評估範圍[L, R] 上的方程式後,可以使用此函數獲得結果,該結果以雙精度值向量形式傳遞-
< /里>vector<double> results = evaluate_equation(1, 10);
登入後複製
double equation(double x) {
return x*x + 2*x + 1;
}
vector<double> evaluate_equation(int L, int R) {
vector<double> results;
for (int x = L; x <= R; x++) {
double y = equation(x);
results.push_back(y);
}
return results;
}
注意 - 透過簡單地用所需的方程式取代方程式函數,就可以改變計算任何方程式的過程。
遵循的方法
方法-1
在 C 中,可以使用循環循環遍歷範圍內的每個值並評估其中的方程,以便評估範圍 [L, R] 中的方程。
範例中評估的範圍是 [1, 10],評估的方程式是 i*i 2*i 1。 for 迴圈重複評估範圍內每個值的方程,並將答案列印到控制台。方程式和範圍可以根據需要進行更改。
範例 1
#include <iostream>
using namespace std;
int main() {
int L = 1, R = 10; // range of values to evaluate
for (int i = L; i <= R; i++) {
int result = i*i + 2*i + 1; // equation to evaluate
cout << "Result at " << i << " = " << result << endl;
}
return 0;
}
輸出
Result at 1 = 4 Result at 2 = 9 Result at 3 = 16 Result at 4 = 25 Result at 5 = 36 Result at 6 = 49 Result at 7 = 64 Result at 8 = 81 Result at 9 = 100 Result at 10 = 121
方法2
這裡是 C 查詢的說明,可用來分析給定方程式的 L 和 R 之間的值範圍 -
在此圖中,需要計算的方程式首先被定義為稱為方程式的函數。然後,我們建立一個評估函數,它接受兩個參數 L 和 R,它們代表我們要評估方程式的值範圍。
我們在評估函數內迭代評估 L 和 R(含)之間的每個值的方程式。然後,使用 cout,我們輸出每個值的結果。
我們在主函數中指定要計算方程式的範圍(在本例中,L = 1 且 R = 10),並使用這些值來呼叫評估函數。程式設計師的輸出將是 1 到 10 之間每個數字的問題的解決方案。
範例 2
#include <bits/stdc++.h>
using namespace std;
// Define the equation you want to evaluate
int equation(int x) {
return x * x + 2 * x + 1;
}
// Define a function to evaluate the equation for a given range [L, R]
void evaluate(int L, int R) {
for (int i = L; i <= R; i++) {
int result = equation(i);
cout << "The result of equation for " << i << " is " << result << endl;
}
}
int main() {
int L = 1, R = 10;
evaluate(L, R);
return 0;
}
輸出
The result of equation for 1 is 4 The result of equation for 2 is 9 The result of equation for 3 is 16 The result of equation for 4 is 25 The result of equation for 5 is 36 The result of equation for 6 is 49 The result of equation for 7 is 64 The result of equation for 8 is 81 The result of equation for 9 is 100 The result of equation for 10 is 121
結論
總之,我們可以應用前綴和或累積和方法來評估區間 [L,R] 內的給定方程式。透過預先計算直到每個索引的方程式值的前綴和,可以在恆定時間內回答每個查詢。此策略的時間複雜度(其中 N 是輸入陣列的大小)對於預計算來說是 O(N),對於每個查詢來說是 O(1)。
總的來說,輸入陣列的大小和要執行的查詢的數量決定了應使用哪種方法。如果查詢的數量遠大於陣列的大小,則前綴和技術會更有效。但是,如果查詢數量較少,二分搜尋策略可能是更好的選擇。
以上是在一個範圍內評估給定方程式的查詢的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 使用java的StringBuilder.replace()函數取代指定範圍的字符
Jul 24, 2023 pm 06:12 PM
使用java的StringBuilder.replace()函數取代指定範圍的字符
Jul 24, 2023 pm 06:12 PM
使用java的StringBuilder.replace()函數取代指定範圍的字元在Java中,StringBuilder類別提供了replace()方法,可以用來取代字串中指定範圍的字元。方法的語法如下:publicStringBuilderreplace(intstart,intend,Stringstr)上面的方法用來取代從索引star
 找出在範圍內不可被任何數整除的數字,使用C++
Sep 13, 2023 pm 09:21 PM
找出在範圍內不可被任何數整除的數字,使用C++
Sep 13, 2023 pm 09:21 PM
在本文中,我們將討論查找1到n(給定)之間的數字的問題,這些數字不能被2到10之間的任何數字整除。讓我們透過一些例子來理解這一點-Input:num=14Output:3Explanation:Therearethreenumbers,1,11,and13,whicharenotdivisible.Input:num=21Output:5Explanation:Therearefivenumbers1,11,13,17,and19,whicharen的解題方法簡單方法如果
 Vue 中如何實現日期範圍選擇器?
Jun 25, 2023 am 08:41 AM
Vue 中如何實現日期範圍選擇器?
Jun 25, 2023 am 08:41 AM
Vue中如何實現日期範圍選擇器?日期範圍選擇器是現代Web應用程式中常用到的一種介面元件。它允許使用者從一個日期範圍中選擇一個日期或一個時間段。對於需求為日期範圍選擇器的網頁應用程式開發,Vue.js是一個非常好的選擇。 Vue.js是一個用於建立使用者介面的漸進式JavaScript框架,它允許開發者使用元件化的方式來建立複雜的互動式介面
 【Python NLTK】文字分類,輕鬆搞定文本歸類難題
Feb 25, 2024 am 10:16 AM
【Python NLTK】文字分類,輕鬆搞定文本歸類難題
Feb 25, 2024 am 10:16 AM
文字分類是自然語言處理(NLP)任務之一,它旨在將文字歸類到預先定義的類別中。文字分類有許多實際應用,例如電子郵件過濾、垃圾郵件偵測、情緒分析和問答系統等。使用pythonNLTK庫完成文字分類的任務可以分為以下幾個步驟:資料預處理:首先,需要對資料進行預處理,包括移除標點符號、轉換成小寫、移除空格等。特徵提取:接下來,需要從預處理後的文字中提取特徵。特徵可以是字詞、詞組或句子。模型訓練:然後,需要使用擷取的特徵來訓練一個分類模型。通常使用的分類模型包括樸素貝葉斯、支援向量機和決策樹等。評估:最後
 評估iqooneo8和iqooneo9:哪一個比較適合?
Mar 25, 2024 am 09:00 AM
評估iqooneo8和iqooneo9:哪一個比較適合?
Mar 25, 2024 am 09:00 AM
21世紀現代社會中,電子產品已成為人們生活中不可或缺的一部分。在這個時代,電子煙也逐漸成為一種受歡迎的消費品。在眾多電子煙品牌中,iqooneo8和iqooneo9這兩款產品備受關注。消費者常常在兩者之間猶豫不決,究竟哪一個比較適合?本文將對這兩款產品進行評估,幫助讀者做出更好的選擇。首先從品牌背景來看,iqooneo8和iqooneo9都屬於IQOS品牌旗
 如何評估和降低MySQL到DB2技術轉型的風險?
Sep 08, 2023 pm 04:10 PM
如何評估和降低MySQL到DB2技術轉型的風險?
Sep 08, 2023 pm 04:10 PM
如何評估和降低MySQL到DB2技術轉型的風險?概述:隨著企業業務的發展和需求的變化,可能出現將MySQL資料庫遷移到DB2資料庫的需求。然而,資料庫遷移本身存在一定的風險,特別是當涉及不同的資料庫技術時。本文將探討如何評估和降低MySQL到DB2技術轉型的風險,並提供一些程式碼範例來幫助讀者更好地理解這個過程。一、風險評估:在進行MySQL到DB2技術轉型
 Java函數在不同場景下的適用性如何評估?
Apr 19, 2024 pm 10:21 PM
Java函數在不同場景下的適用性如何評估?
Apr 19, 2024 pm 10:21 PM
評估Java函數適用性時,需考慮函數類型、輸入輸出、效能、易用性。在驗證郵箱有效性時,純函數isValidEmail()滿足需求;查找清單最大值時,雜函數findMax()適用,但修改輸入需注意;連接字串時,純函數concatStrings()便捷高效。
 深度估計SOTA!自動駕駛單眼與環視深度的自適應融合
Mar 23, 2024 pm 01:06 PM
深度估計SOTA!自動駕駛單眼與環視深度的自適應融合
Mar 23, 2024 pm 01:06 PM
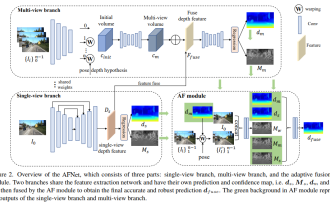
寫在前面&個人理解多視圖深度估計在各種基準測試中都取得了較高性能。然而,目前幾乎所有的多視圖系統都依賴給定的理想相機姿態,而這在許多現實世界的場景中是不可用的,例如自動駕駛。本工作提出了一種新的穩健性基準來評估各種噪音姿態設定下的深度估計系統。令人驚訝的是,發現當前的多視圖深度估計方法或單視圖和多視圖融合方法在給定有雜訊的姿態設定時會失敗。為了應對這一挑戰,這裡提出了一種單視圖和多視圖融合的深度估計系統AFNet,該系統自適應地整合了高置信度的多視圖和單視圖結果,以實現穩健和準確的深度估計。自






