最大的内接于一个半圆内的正方形内的魯拉曲线三角形是什么?
在這裡,我們將看到一個正方形內切於一個半圓的最大盧卡斯三角形的面積。假設半圓的半徑為R,正方形的邊長為‘a’,盧卡斯三角形的高度為h。
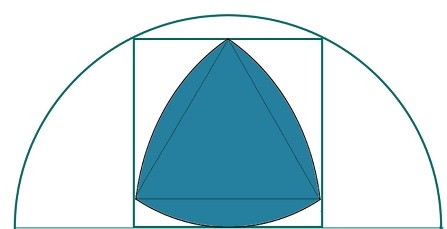
我們知道正方形內切於一個半圓的邊長為-
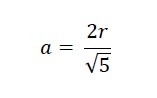
盧卡斯三角形的高度與邊長相等。所以a = h。因此盧卡斯三角形的面積為-
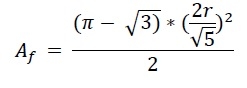
#範例
#include <iostream>
#include <cmath>
using namespace std;
float areaReuleaux(float r) { //radius of the semicircle is r
if (r < 0) //if r is negative it is invalid
return -1;
float area = ((3.1415 - sqrt(3)) * (2*r/(sqrt(5))) * (2*r/(sqrt(5))))/2;
return area;
}
int main() {
float rad = 8;
cout << "Area of Reuleaux Triangle: " << areaReuleaux(rad);
}輸出
Area of Reuleaux Triangle: 36.0819
以上是最大的内接于一个半圆内的正方形内的魯拉曲线三角形是什么?的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 C#與C:歷史,進化和未來前景
Apr 19, 2025 am 12:07 AM
C#與C:歷史,進化和未來前景
Apr 19, 2025 am 12:07 AM
C#和C 的歷史與演變各有特色,未來前景也不同。 1.C 由BjarneStroustrup在1983年發明,旨在將面向對象編程引入C語言,其演變歷程包括多次標準化,如C 11引入auto關鍵字和lambda表達式,C 20引入概念和協程,未來將專注於性能和系統級編程。 2.C#由微軟在2000年發布,結合C 和Java的優點,其演變注重簡潔性和生產力,如C#2.0引入泛型,C#5.0引入異步編程,未來將專注於開發者的生產力和雲計算。
 C#vs. C:學習曲線和開發人員的經驗
Apr 18, 2025 am 12:13 AM
C#vs. C:學習曲線和開發人員的經驗
Apr 18, 2025 am 12:13 AM
C#和C 的学习曲线和开发者体验有显著差异。1)C#的学习曲线较平缓,适合快速开发和企业级应用。2)C 的学习曲线较陡峭,适用于高性能和低级控制的场景。
 C社區:資源,支持和發展
Apr 13, 2025 am 12:01 AM
C社區:資源,支持和發展
Apr 13, 2025 am 12:01 AM
C 學習者和開發者可以從StackOverflow、Reddit的r/cpp社區、Coursera和edX的課程、GitHub上的開源項目、專業諮詢服務以及CppCon等會議中獲得資源和支持。 1.StackOverflow提供技術問題的解答;2.Reddit的r/cpp社區分享最新資訊;3.Coursera和edX提供正式的C 課程;4.GitHub上的開源項目如LLVM和Boost提陞技能;5.專業諮詢服務如JetBrains和Perforce提供技術支持;6.CppCon等會議有助於職業
 C和XML:探索關係和支持
Apr 21, 2025 am 12:02 AM
C和XML:探索關係和支持
Apr 21, 2025 am 12:02 AM
C 通過第三方庫(如TinyXML、Pugixml、Xerces-C )與XML交互。 1)使用庫解析XML文件,將其轉換為C 可處理的數據結構。 2)生成XML時,將C 數據結構轉換為XML格式。 3)在實際應用中,XML常用於配置文件和數據交換,提升開發效率。
 超越炒作:評估當今C的相關性
Apr 14, 2025 am 12:01 AM
超越炒作:評估當今C的相關性
Apr 14, 2025 am 12:01 AM
C 在現代編程中仍然具有重要相關性。 1)高性能和硬件直接操作能力使其在遊戲開發、嵌入式系統和高性能計算等領域佔據首選地位。 2)豐富的編程範式和現代特性如智能指針和模板編程增強了其靈活性和效率,儘管學習曲線陡峭,但其強大功能使其在今天的編程生態中依然重要。
 C的未來:改編和創新
Apr 27, 2025 am 12:25 AM
C的未來:改編和創新
Apr 27, 2025 am 12:25 AM
C 的未來將專注於並行計算、安全性、模塊化和AI/機器學習領域:1)並行計算將通過協程等特性得到增強;2)安全性將通過更嚴格的類型檢查和內存管理機制提升;3)模塊化將簡化代碼組織和編譯;4)AI和機器學習將促使C 適應新需求,如數值計算和GPU編程支持。
 什麼是C 中的靜態分析?
Apr 28, 2025 pm 09:09 PM
什麼是C 中的靜態分析?
Apr 28, 2025 pm 09:09 PM
靜態分析在C 中的應用主要包括發現內存管理問題、檢查代碼邏輯錯誤和提高代碼安全性。 1)靜態分析可以識別內存洩漏、雙重釋放和未初始化指針等問題。 2)它能檢測未使用變量、死代碼和邏輯矛盾。 3)靜態分析工具如Coverity能發現緩衝區溢出、整數溢出和不安全API調用,提升代碼安全性。
 C 中的chrono庫如何使用?
Apr 28, 2025 pm 10:18 PM
C 中的chrono庫如何使用?
Apr 28, 2025 pm 10:18 PM
使用C 中的chrono庫可以讓你更加精確地控制時間和時間間隔,讓我們來探討一下這個庫的魅力所在吧。 C 的chrono庫是標準庫的一部分,它提供了一種現代化的方式來處理時間和時間間隔。對於那些曾經飽受time.h和ctime折磨的程序員來說,chrono無疑是一個福音。它不僅提高了代碼的可讀性和可維護性,還提供了更高的精度和靈活性。讓我們從基礎開始,chrono庫主要包括以下幾個關鍵組件:std::chrono::system_clock:表示系統時鐘,用於獲取當前時間。 std::chron






