N元樹中的同構性
同構被定義為兩棵樹具有相同或鏡像結構。在鏡像結構的情況下,左節點的資料將始終與右節點相符。例如,我們將取一個最接近鏡像的數字,看看它的反向是什麼,這就是同構的真正概念。
在本文中,我們將檢查兩個不同的二元樹是否同構。
讓我們以N叉樹的同構為例-

請注意,L代表左節點,而R代表右節點
左側最左第二分區的P和Q樹的鏡像結構

這兩個圖示展示了它們如何透過給出四個匹配條件(P和Q的根節點)來彼此同構。
左-左節點可以匹配。
要嘛可以匹配右-右節點。
左右節點皆可配對。
要嘛右左無法匹配。
文法
程式中使用了以下語法−
struct name_of_structure{
data_type var_name;
// data member or field of the structure.
}
參數
struct − 這個關鍵字用來表示結構資料型態。
name_of_structure − 我們為結構提供任何名稱。
結構是將各種相關變數集中在一個地方的集合。
演算法
我們將使用一個名為‘iostream’的頭檔來開始程式。
我們正在建立一個名為'tree_node'的結構,其中包含整數型別'd'和初始化指標變數- 'l'和'r',分別表示左右子節點的資料。
現在我們使用一個名為'create_node()'的函數來建立另一個結構,該函數接受一個名為'data'的參數來指定根節點的值。同時,我們建立一個名為‘tree_node’的指針,並使用給定的資料來初始化左子節點和右子節點的指標為空,並傳回根節點。使用這個函數,我們將插入左子節點和右子節點的節點。
我們正在建立一個名為'check_isomorphism_tree 的函數,它使用布林資料類型,以兩個tree_node指標p和q作為輸入參數,並傳回一個布林值。在其中,我們兩次創建一個「if語句」來檢查p中的資料是否等同於q中的資料。
檢查p和q是否都為null,如果是,則傳回true,因為樹是同構的。
檢查 p 或 q 中是否有任何一個為 null,如果是,則傳回 false,因為這兩棵樹不是同構的。
在'check_isomorphism_tree'函數中,我們使用邏輯運算子「&&」和「||」遞歸檢查節點'p'和'q '的所有可能的左右子節點組合。
我們從主函數開始,建立兩個樹節點「p」和「q」來提供資訊。
在主函數中,我們使用if語句呼叫‘check_isomorphism_tree’函數,並傳遞給定的參數p和q來驗證這些整數值是否同構。如果它們是同構的,則列印語句為“這個給定的節點資訊將產生同構樹”,否則相反。
Example
的中文翻譯為:範例
在這個程式中,我們將檢查兩個二元樹是否同構。
#include<iostream>
using namespace std;
struct tree_node{
int d;
tree_node*l; // l = left
tree_node*r; // r = right
};
struct tree_node* create_node(int data){
struct tree_node*root= new tree_node;
root->d= data;
root->l= NULL;
root->r= NULL;
return root;
}
bool check_isomorphism_tree(tree_node*p, tree_node*q) {
// p and q both are different tree
if(p==NULL and q==NULL){
return true;
}
if(p==NULL or q==NULL){
return false;
}
// return all the possible condition
return (p->d==q->d && ((check_isomorphism_tree(p->l,q->r)&& check_isomorphism_tree(p->r,q->l))||(check_isomorphism_tree(p->l,q->l)&& check_isomorphism_tree(p->r,q->r))));
}
int main(){
// Tree of root p
struct tree_node *p = create_node(10);
p->l = create_node(5);
p->r = create_node(4);
p->l->l = create_node(11);
p->r->r = create_node(12);
p->l->r = create_node(51);
p->r->l = create_node(6);
p->l->r->l = create_node(7); // left->right->left
p->l->l->l = create_node(9); // left->left->left
// Tree of root q
struct tree_node *q = create_node(10);
q->l = create_node(5);
q->r = create_node(4);
q->l->l = create_node(11);
q->r->r = create_node(12);
q->l->r = create_node(51);
q->r->l = create_node(6);
q->l->r->l = create_node(7);
q->l->l->l = create_node(9);
if(check_isomorphism_tree(p,q)){
cout<<"This given information of node will make isomorphism tree"<<endl;
} else {
cout<<" This given information of node will not make isomorphism tree "<<endl;
}
return 0;
}
輸出
This given information of node will make isomorphism tree
結論
在這個程式中,我們了解N叉樹中同構的概念。我們看到如何使用結構來表示樹節點,以及使用左-左節點、右-左節點、左-右-左節點等來建構樹,以下操作有助於滿足樹的同構性質。
以上是N元樹中的同構性的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 如何修改Win10記事本的檔案副檔名
Jan 04, 2024 pm 12:49 PM
如何修改Win10記事本的檔案副檔名
Jan 04, 2024 pm 12:49 PM
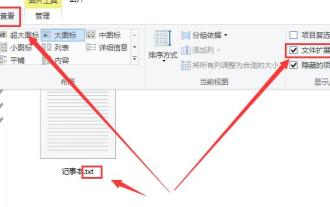
在使用記事本的時候,我們因為需要處理的事情不同,時長會需要更改記事本的擴展名,那麼擴展名需要怎麼去更改呢,其實只需要使用重命名功能就能修改擴展名了。 win10記事本的副檔名怎麼改:1、我們在資料夾中,先點選上方的,勾選上。 2.這樣檔案的副檔名就能顯示出來了,然後右鍵你的記事本,選擇3、選取.後面的進行更改。 4、如改成.jpeg格式的。然後會彈出提示,點選。 5、更改完成了,就是這樣的了。
 如何將HTML轉換為MP4格式
Feb 19, 2024 pm 02:48 PM
如何將HTML轉換為MP4格式
Feb 19, 2024 pm 02:48 PM
標題:HTML如何轉換為MP4格式:詳細程式碼範例在日常的網頁製作過程中,我們常常會遇到將HTML頁面或特定的HTML元素轉換為MP4影片的需求。例如將動畫效果、投影片或其他動態元素儲存為影片檔案。本文將介紹如何使用HTML5和JavaScript將HTML轉換為MP4格式,並提供具體的程式碼範例。 HTML5的video標籤和CanvasAPIHTML5引入
 呼叫SQL觸發器執行外部程序
Feb 18, 2024 am 10:25 AM
呼叫SQL觸發器執行外部程序
Feb 18, 2024 am 10:25 AM
標題:SQL觸發器呼叫外部程式的特定程式碼範例正文:在使用SQL觸發器時,有時需要呼叫外部程式來處理一些特定的操作。本文將介紹如何在SQL觸發器中呼叫外部程序,並給出特定的程式碼範例。一、建立觸發器首先,我們需要建立一個觸發器來監聽資料庫中的某個事件。這裡以「訂單表(order_table)」為例,當有新的訂單被插入時,觸發器就會被激活,然後呼叫外部程式進行一
 提取Dump檔案的方法
Feb 19, 2024 pm 12:15 PM
提取Dump檔案的方法
Feb 19, 2024 pm 12:15 PM
抓取Dump檔案的方法在電腦系統中,Dump檔案是一個記錄系統運作狀態和資料的檔案。在軟體開發和系統故障排查中,抓取Dump檔案可以幫助程式開發人員和系統管理員分析和診斷各種問題,例如程式崩潰、記憶體洩漏以及系統異常等。本文將介紹一些常見的方法和工具來抓取Dump檔案。一、Windows系統下抓取Dump檔案的方法使用任務管理器:在Windows作業系統中,
 Windows 12發布日期
Jan 05, 2024 pm 05:24 PM
Windows 12發布日期
Jan 05, 2024 pm 05:24 PM
先前win11正式發布,讓不少用戶已經開始暢享win12了,想知道win12什麼時候發布的,其實根據規律來看它將在2024年左右發布。 win12什麼時候發布的:答:win12預計在2024年秋季左右發布。 1.根據微軟最新的爆料資訊來看,win12預計會在2024秋季進行發布。 2.而這次的win12將會有多個全新的設計概念,在整潔視覺上會有更多的提升。 3.最新的開發者會上,微軟的開發員工就爆料將要製作一個浮動的任務欄,讓任務欄有一種浮動的感覺。
 如何調整Windows 7桌面顯示比例
Dec 27, 2023 am 08:13 AM
如何調整Windows 7桌面顯示比例
Dec 27, 2023 am 08:13 AM
使用win7的小夥伴非常的多,在電腦上看影片或是資料的時候都會需要進行比例的調整吧,那該怎麼去調整呢?下面就來看看詳細的設定方法吧。 win7桌面顯示比例怎麼設定:1、點選左下角電腦開啟「控制台」。 2、隨後在控制面板中找到「外觀」。 3.進入外觀後點選「顯示」。 4、隨後即可依需求顯示的效果進行桌面的大小顯示調整。 5.也可以點選左側的「調整解析度」。 6.透過更改螢幕解析度來調整電腦桌面的比例。
 NVIDIA控制面板的作用是什麼?
Feb 19, 2024 pm 03:59 PM
NVIDIA控制面板的作用是什麼?
Feb 19, 2024 pm 03:59 PM
NVIDIA控制面板是幹嘛的隨著電腦科技發展的日新月異,顯示卡的重要性越來越大。而NVIDIA作為全球著名的顯示卡製造商之一,其控制面板更是備受矚目。那麼,NVIDIA控制面板究竟是做什麼的呢?本文將為大家詳細介紹NVIDIA控制面板的功能與用途。首先,我們來了解NVIDIA控制面板的概念與定義。 NVIDIA控制面板是用於管理和配置顯示卡相關設定的軟體。
 比較PyCharm社群版和專業版的功能
Feb 25, 2024 am 09:54 AM
比較PyCharm社群版和專業版的功能
Feb 25, 2024 am 09:54 AM
PyCharm是由JetBrains公司開發的一個以Python開發的整合開發環境(IDE),目前有社群版和專業版兩個版本。對於許多Python開發者來說,選擇合適的PyCharm版本是非常重要的,因為功能特性的不同可能會影響開發效率和體驗。以下將對PyCharm社群版和專業版的功能特性進行比較,幫助開發者選擇適合自己的版本。首先,PyCharm社群版是免






