圖的一個主導集合是NP完全問題，它是頂點的子集，使得子集中的每個頂點或相鄰的頂點都在子集中。 NP的完整形式是“非確定性多項式”，它將在多項式時間內檢查問題，這意味著我們可以在多項式時間內檢查解決方案是否正確。多項式時間對於像線性搜尋的時間複雜度– n， 二分搜尋– logn， 歸併排序- n(log)n 等程式碼具有最好的複雜性。 NP完全圖在合理的時間內提供了一個很好的解決方案。這個應用程式在網路控制、電腦實驗室中的拓撲創建、社交網路和分散式運算等領域中使用。
讓我們理解並檢查節點是否具有 NP 完全圖的主導集。
據說一個頂點支配它自己和它的每個鄰居。
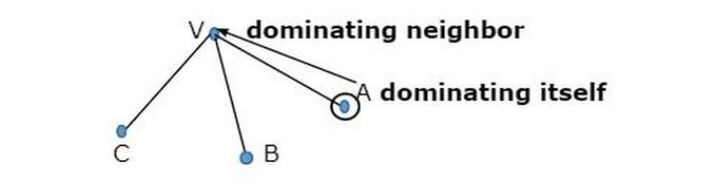
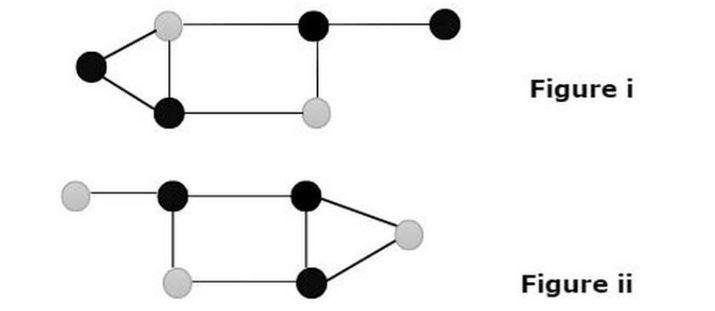
##我們看到有兩個圖顯示了圖中節點的灰色在自然界中占主導地位。
G = V, E
參數
G 被視為圖，V 被視為頂點，E 被視為邊。
給定一個圖G(V, E)和一個整數k，確定圖是否有一個大小為k的支配集。被指定為問題的輸入被認為是問題的一個實例。圖G(V, E)和整數k作為支配集問題的範例，該問題詢問圖G是否可以有一個在G中的支配集。由於NP-完全問題的定義是同時屬於NP和NP-困難的問題，所以證明一個問題是NP-完全的有兩個組成部分−
如果有一個 NP 問題 Y 在多項式時間內可簡化為 X，則 X 是 NP 完全問題。 NP 完全問題與 NP 問題一樣困難。如果一個問題同時是 NP 問題和 NP-Hard 問題的一部分，那麼它就是 NP-Complete。在多項式時間內，非確定性圖靈機可以解決 NP 完全問題。當一個問題是 np 完全問題時，它同時具有 np 和 np 硬組合。
這意味著具有np解的問題可以在多項式時間內進行驗證。
NP完全的真實例子具有支配集，例如 -
決策問題。
圖形一致。
NP_search( key ) {
arraylist[100];
i = array_check(key);
if(list[i]==key) {
searching found at index i.
} else {
searching found at index i.
}
}
因此，演算法的總時間複雜度為 O(1)，但我們不知道哪種搜尋技術對解決該問題更有用，這稱為非確定性演算法。
如果存在一個可在多項式時間內歸約到問題X的NP-完全問題Y，那麼問題X是NP-困難的。 NP-困難問題與NP-完全問題一樣難。一個NP-困難問題不一定屬於NP類。
如果每個 NP 問題都可以在多項式時間內解決，則稱為 NP-Hard。很多時候，一個特定的問題是用來解決和減少其他問題的。
NP-hard 的真實例子具有支配集，例如 -
哈密頓迴路
#最佳化問題
最短路線
我們學習了圖的主導集合是 NP 完全的概念。我們看到離散數學如何成為連結這些問題的重要方面，例如哈密爾頓循環、最短路徑等。在程式設計方面，NP 完全問題是一類很難找到但可以直接驗證解決方案的問題多項式時間。
以上是證明圖的主導集合是NP-完全的的詳細內容。更多資訊請關注PHP中文網其他相關文章！
