使用佛洛伊德-沃沙爾演算法找到任兩個節點之間的最短路徑

C 有一個宏，它被定義為一段程式碼或期望的值，並且每當使用者需要時，它將被重複使用。佛洛伊德-沃爾夏爾演算法是在給定的加權圖中找到所有頂點對之間最短路徑的過程。該演算法遵循動態規劃的方法來找到最小權重圖。

讓我們透過圖表來理解佛洛伊德-沃爾夏爾演算法的意義 -

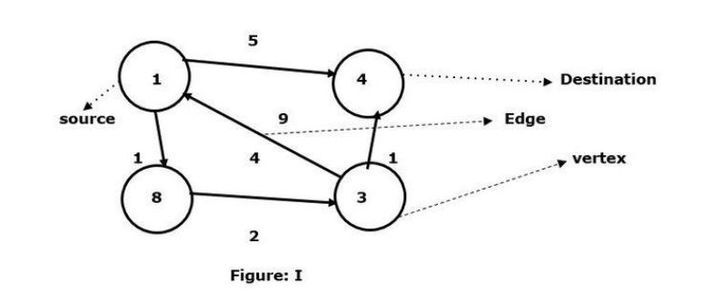
以頂點1為來源，頂點4為目的地，求它們之間的最短路徑。

我們已經看到有兩條路徑可以連接到目標頂點4。

• 1 -> 4 – 邊的權重為5

• 1 -> 8 -> 3 -> 4 – 邊權重（1 2 1）為4。

在給定的圖 I 中，我們看到兩個頂點之間連接的最小邊。所以這裡頂點 8 和頂點 3 連接頂點 1 到頂點 4 的路徑以及邊是4。另一方面，頂點1到頂點4之間有一條有向邊，邊的權重為5。

現在我們比較兩個權重，即4和5。因此，這裡 4 是根據 Floyd Warshall 演算法計算的圖的最小權重。

在本文中，我們將使用 Floyd Warshall 演算法求解任兩個給定節點之間的最短路徑。

文法

以下語法用於程式中 -

data_type[][] array_name;

參數

data_type[][] - 使用者提到的資料類型。第一個陣列代表行，第二個陣列代表列。所以，這代表了二維數組。

array_name - 為陣列指定的名稱。

演算法

• 我們將使用頭檔'iostream' 啟動程序，並將巨集位置定義為'INF'（無限大），因為稍後它將滿足二維數組矩陣和if-else 語句。

• 接下來，我們建立名為'printPath' 的全域函數定義，並接受三個參數，分別是'parent[]'、'i' 和'j' 驗證路徑是否存在。

• 然後我們開始主函數，並將值‘4’儲存到變數‘V’中，該變數表示頂點的數量。其次，將值以鄰接矩陣的形式儲存到變數‘dist[V][V]’。如我們所知，dist[i][j]表示2D矩陣，它定義了從'i'到'j'的邊的權重，透過儲存鄰接矩陣。

• 接下來，我們正在為變數‘parent’初始化2D數組，並且大小為[V][V]。

在這個變數中，我們用來顯示每對頂點'i' 和'j' w.r.t 'parent[i][j]'< /b> .

• 透過使用兩個巢狀的for循環，我們將找到最短路徑。第一個for迴圈迭代矩陣中的行。然後，透過第二個for迴圈迭代矩陣中的列，然後我們將使用if-else語句檢查以下條件 -

• #如果 (dist[i][j] != INF && i != j) { parent[i][j] = i;}

  的中文翻譯為：parent[i][j] = i;}

  在if語句中，我們使用'and' (&&)運算子來表示兩個條件，如果這兩個條件都滿足，那麼'i'將被儲存到'parent[i ][j]'中，從而驗證路徑存在。

• 其他{ parent[i][j] = -1;}

  的中文翻譯為：parent[i][j] = -1;}

  在 else 語句中，我們將「-1」初始化為「parent[i][j]」，以驗證路徑不存在。

• 現在我們從三個嵌套的for 迴圈開始，並在0 到V-1 的範圍內應用k 個頂點，在這個範圍的幫助下，我們的最短距離和路徑將被更新。在第三個巢狀循環中，我們使用以下條件，例如

if (dist[i][j] < dist[i][k] + dist[k][j]){
   dist[i][j] = dist[i][k] + dist[k][j]; 
   parent[i][j] = parent[k][j];	
}

這裡 K 正在更新二維數組矩陣中的行和列的部分，這驗證了新更新的最短路徑和距離。

• 接下來，我們透過給定以下條件，列印出所有頂點對的最短距離和路徑

• #透過使用兩個巢狀的 for 循環，我們列印最短距離和路徑。

• 透過在第二個for迴圈下使用if語句，我們將檢查dist[i][j]是否等於無限大。如果發現它是無窮大，則列印“INF”，否則列印最短路徑。

• 最後，我們呼叫名為'printPath()' 的函數，透過傳遞三個參數（parent[i]、i、和j。

範例

在這個程式中，我們將使用Floyd Warshall演算法計算任兩個節點之間的最短路徑。

#include <iostream> 
using namespace std; 
#define INF 1000000000 // Infinity

void printPath(int parent[], int i, int j) {
   if (i == j) 
      cout << i << " "; 
   else if (parent[j] == -1) 
     cout << "No path exists"; 
   else
   { 
      printPath(parent, i, parent[j]); 
      cout << j << " "; 
   }
} 

int main() 
{
   int V = 4; 
   // V represent number of vertices
   int dist[V][V] = {{0, 2, INF, 4}, 
      {6, 0, 5, 3}, 
      {INF, 10, 0, 1}, 
      {7, 9, 8, 0}}; 
   // Represent the graph using adjacency matrix

   // Apply the Floyd Warshall algorithm to find the shortest paths
   int parent[V][V];
   for (int i = 0; i < V; i++) 
   { 
      for (int j = 0; j < V; j++) 
      {
         if (dist[i][j] != INF && i != j)
         parent[i][j] = i;
         else
         parent[i][j] = -1;
      }
   }
   // update the path and distance using the k vertex range from 0 to V-1.
   for (int k = 0; k < V; k++) 
   { 
      for (int i = 0; i < V; i++) 
      { 
         for (int j = 0; j < V; j++) 
         { 
            if (dist[i][j] > dist[i][k] + dist[k][j]) 
            {
               dist[i][j] = dist[i][k] + dist[k][j];
               parent[i][j] = parent[k][j];	
            }
         }
      }
   }

   // Print shortest distances and paths between all pairs of vertices
   for (int i = 0; i < V; i++) 
   { 
      for (int j = 0; j < V; j++) 
      { 
         cout << "The Shortest distance between " << i << " and " << j << " is ";
         if (dist[i][j] == INF) 
            cout << "INF "; 
         else
            cout << dist[i][j] << " ";

         cout << "and the shortest path is:- ";
         printPath(parent[i], i, j);
         cout << endl;
      } 
   } 

   return 0; 
}

输出

The Shortest distance between 0 and 0 is 0 and the shortest path is:- 0 
The Shortest distance between 0 and 1 is 2 and the shortest path is:- 0 1 
The Shortest distance between 0 and 2 is 7 and the shortest path is:- 0 1 2 
The Shortest distance between 0 and 3 is 4 and the shortest path is:- 0 3 
The Shortest distance between 1 and 0 is 6 and the shortest path is:- 1 0 
The Shortest distance between 1 and 1 is 0 and the shortest path is:- 1 
The Shortest distance between 1 and 2 is 5 and the shortest path is:- 1 2 
The Shortest distance between 1 and 3 is 3 and the shortest path is:- 1 3 
The Shortest distance between 2 and 0 is 8 and the shortest path is:- 2 3 0 
The Shortest distance between 2 and 1 is 10 and the shortest path is:- 2 1 
The Shortest distance between 2 and 2 is 0 and the shortest path is:- 2 
The Shortest distance between 2 and 3 is 1 and the shortest path is:- 2 3 
The Shortest distance between 3 and 0 is 7 and the shortest path is:- 3 0 
The Shortest distance between 3 and 1 is 9 and the shortest path is:- 3 1 
The Shortest distance between 3 and 2 is 8 and the shortest path is:- 3 2 
The Shortest distance between 3 and 3 is 0 and the shortest path is:- 3 

结论

我们学习了使用Floyd Warshall算法找到任意两个节点之间的最短路径的概念。我们使用邻接矩阵作为程序的输入，通过它我们找到了最短路径和距离。此外，为了更新路径和距离，我们使用了k个顶点来更新行和列。在我们的日常生活中，我们在谷歌地图上搜索最短路线或路径，从一个起点到目的地。

以上是使用佛洛伊德-沃沙爾演算法找到任兩個節點之間的最短路徑的詳細內容。更多資訊請關注PHP中文網其他相關文章！