如何使用動態規劃演算法在PHP中解決背包問題並獲得最佳解?

如何使用動態規劃演算法在PHP中解決背包問題並獲得最佳解?
背包問題是電腦科學中經典的組合最佳化問題之一。在給定一組物品和一個背包的容量下,如何選擇物品放入背包,使得背包中物品的總價值最大化,是背包問題需要解決的核心。
動態規劃是解決背包問題的常用方法之一。它透過將問題拆分成子問題,並保存子問題的解,最終得到最適解。以下我們將詳細說明如何使用動態規劃演算法在PHP中實現背包問題的求解。
首先,我們需要定義背包問題的輸入和輸出:
#輸入:
- 物品的重量數組$weights,$weights[$i] 表示第$i 個物品的重量
- 物品的價值數組$values,$values[$i] 表示第$i 個物品的價值
- 背包的容量$capacity,表示背包的最大容量
#輸出:
- 背包中物品的最大總價值
接下來,我們需要定義一個二維陣列$dp,用來保存子問題的解。 $dp[$i][$j] 表示在前 $i 個物品中,背包容量為 $j 時的最大總價值。
演算法的流程如下:
- 初始化 $dp 數組,將所有元素設為 0。
-
外層循環遍歷物品的索引,從$i = 1 到$i = count($weights) - 1:
-
內層循環遍歷背包的容量,從$j = 0 到$j = $capacity:
- 如果當前物品的重量$weights[$i] 大於背包的容量$j,則$dp[$i] [$j] = $dp[$i - 1][$j],即當前物品無法放入背包,最大總價值與前$i - 1 個物品相同。
- 否則,當前物品可以放入背包,將其產生的價值$values[$i] 加上放入該物品之前的最大總價值$dp[$i - 1][$j - $ weights[$i]],與目前價值相比,取較大值為$dp[$i][$j]。
-
- 返回$dp[count($weights) - 1][$capacity],即前count($weights) 個物品在背包容量為$capacity時的最大總價值。
以下是使用PHP程式碼實作背包問題的動態規劃演算法:
function knapsack($weights, $values, $capacity) {
$dp = [];
for ($i = 0; $i < count($weights); $i++) {
$dp[$i] = [];
for ($j = 0; $j <= $capacity; $j++) {
$dp[$i][$j] = 0;
}
}
for ($i = 1; $i < count($weights); $i++) {
for ($j = 0; $j <= $capacity; $j++) {
if ($weights[$i] > $j) {
$dp[$i][$j] = $dp[$i - 1][$j];
} else {
$dp[$i][$j] = max($dp[$i - 1][$j], $values[$i] + $dp[$i - 1][$j - $weights[$i]]);
}
}
}
return $dp[count($weights) - 1][$capacity];
}#使用上述程式碼,我們可以透過呼叫knapsack($weights, $values, $capacity ) 函數來求解背包問題,並獲得最佳解。
希望這篇文章能幫助你理解如何使用動態規劃演算法在PHP中解決背包問題並獲得最佳解。
以上是如何使用動態規劃演算法在PHP中解決背包問題並獲得最佳解?的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

熱門話題
 如何使用C#撰寫動態規劃演算法
Sep 20, 2023 pm 04:03 PM
如何使用C#撰寫動態規劃演算法
Sep 20, 2023 pm 04:03 PM
如何使用C#撰寫動態規劃演算法摘要:動態規劃是求解最最佳化問題的常用演算法,適用於多種場景。本文將介紹如何使用C#編寫動態規劃演算法,並提供具體的程式碼範例。一、什麼是動態規劃演算法動態規劃(DynamicProgramming,簡稱DP)是一種用來求解具有重疊子問題和最優子結構性質的問題的演算法想法。動態規劃將問題分解成若干個子問題來求解,透過記錄每個子問題的解,
 PHP演算法解析:如何使用動態規劃演算法解決最長回文子字串問題?
Sep 19, 2023 pm 12:19 PM
PHP演算法解析:如何使用動態規劃演算法解決最長回文子字串問題?
Sep 19, 2023 pm 12:19 PM
PHP演算法解析:如何使用動態規劃演算法解決最長回文子字串問題?動態規劃(DynamicProgramming)是一種常用的演算法思想,可以解決許多複雜的問題。其中之一是最長回文子字串問題,即求字串中最長的回文子字串的長度。本文將介紹如何使用PHP編寫動態規劃演算法來解決這個問題,並提供具體的程式碼範例。先來定義一下最長回文子字串。回文字串是指正反讀都一樣的字串,而回
 如何使用C#撰寫背包問題演算法
Sep 19, 2023 am 09:21 AM
如何使用C#撰寫背包問題演算法
Sep 19, 2023 am 09:21 AM
如何使用C#編寫背包問題演算法背包問題(KnapsackProblem)是一個經典的組合最佳化問題,它描述了一個給定容量的背包以及一系列物品,每個物品都有自己的價值和重量。目標是找到一種最佳策略,使得在不超過背包容量的情況下,裝入背包的物品總價值最大。在C#中,可以透過動態規劃方法來解決背包問題。具體實作如下:usingSystem;namespace
 如何使用C++中的背包問題演算法
Sep 21, 2023 pm 02:18 PM
如何使用C++中的背包問題演算法
Sep 21, 2023 pm 02:18 PM
如何使用C++中的背包問題演算法背包問題是電腦演算法中經典的問題之一,它涉及在給定的背包容量下,如何選擇一些物品放入背包,使得物品的總價值最大化。本文將詳細介紹如何使用C++中的動態規劃演算法來解決背包問題,並給出具體的程式碼範例。首先,我們需要定義背包問題的輸入和輸出。輸入包括物品的重量數組wt[],物品的價值數組val[],以及背包的容量W。輸出為選擇哪些物
 如何使用動態規劃演算法在PHP中解決背包問題並獲得最佳解?
Sep 21, 2023 am 10:33 AM
如何使用動態規劃演算法在PHP中解決背包問題並獲得最佳解?
Sep 21, 2023 am 10:33 AM
如何使用動態規劃演算法在PHP中解決背包問題並獲得最佳解?背包問題是計算機科學中經典的組合最佳化問題之一。在給定一組物品和一個背包的容量下,如何選擇物品放入背包,使得背包中物品的總價值最大化,是背包問題需要解決的核心。動態規劃是解決背包問題的常用方法之一。它透過將問題拆分成子問題,並保存子問題的解,最終得到最適解。以下我們將詳細說明如何使用動態規劃演算法在PHP中
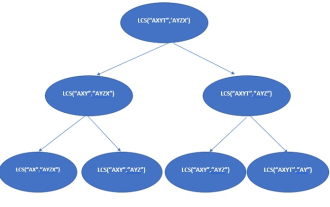 在Java中的記憶化(1D,2D和3D)動態規劃
Aug 23, 2023 pm 02:13 PM
在Java中的記憶化(1D,2D和3D)動態規劃
Aug 23, 2023 pm 02:13 PM
記憶化是一種基於動態規劃的技術,用於透過確保方法不會對相同的輸入集合運行多次來改進遞歸演算法的性能,透過記錄提供的輸入的結果(儲存在數組中)。可以透過實現遞歸方法的自頂向下的方法來實現記憶化。讓我們透過基本的斐波那契數列範例來理解這種情況。 1-D記憶化我們將考慮一個只有一個非常量參數(只有一個參數的值會改變)的遞歸演算法,因此這個方法稱為1-D記憶化。以下程式碼是用來找出斐波那契數列中第N個(所有項直到N)的。範例publicintfibonacci(intn){ &nb
 PHP中的動態規劃演算法詳解
Jul 07, 2023 am 10:48 AM
PHP中的動態規劃演算法詳解
Jul 07, 2023 am 10:48 AM
PHP中的動態規劃演算法詳解動態規劃(DynamicProgramming)是一種解決問題的演算法思想,它透過將問題分解為更小的子問題,並利用已解決的子問題的結果來求解整體問題。在PHP中,動態規劃演算法可以廣泛應用於許多電腦科學和數學領域,例如最短路徑、字串匹配和背包問題等。本文將詳細介紹PHP中的動態規劃演算法原理,並提供程式碼範例進行說明。一、動態規劃算
 如何用PHP實作背包問題演算法
Jul 09, 2023 am 09:15 AM
如何用PHP實作背包問題演算法
Jul 09, 2023 am 09:15 AM
如何用PHP實現背包問題演算法背包問題是一個經典的組合最佳化問題,它的目標是在限定的背包容量下,選取一組物品使得其總價值最大化。在本文中,我們將介紹如何使用PHP來實作背包問題的演算法,並提供對應的程式碼範例。背包問題的描述背包問題可以用以下方式描述:給定一個背包容量C,以及N個物品。每個物品i都有一個重量wi和一個價值vi。要求從這N個物品中選擇一些物品,使得它們






