更通用、有效,螞蟻自研優化器WSAM入選KDD Oral
深度神经网络(DNNs)的泛化能力与极值点的平坦程度密切相关,因此出现了 Sharpness-Aware Minimization (SAM) 算法来寻找更平坦的极值点以提高泛化能力。本文重新审视 SAM 的损失函数,提出了一种更通用、有效的方法 WSAM,通过将平坦程度作为正则化项来改善训练极值点的平坦度。通过在各种公开数据集上的实验表明,与原始优化器、SAM 及其变体相比,WSAM 在绝大多数情形都实现了更好的泛化性能。WSAM 在蚂蚁内部数字支付、数字金融等多个场景也被普遍采用并取得了显著效果。该文被 KDD '23 接收为 Oral Paper。

- 论文地址:https://arxiv.org/pdf/2305.15817.pdf
- 代码地址:https://github.com/intelligent-machine-learning/dlrover/tree/master/atorch/atorch/optimizers
随着深度学习技术的发展,高度过参数化的 DNNs 在 CV 和 NLP 等各种机器学习场景下取得了巨大的成功。虽然过度参数化的模型容易过拟合训练数据,但它们通常具有良好的泛化能力。泛化的奥秘受到越来越多的关注,已成为深度学习领域的热门研究课题。
最新的研究显示,泛化能力与极值点的平坦程度密切相关。换句话说,损失函数的“地貌”中存在平坦的极值点可以实现更小的泛化误差。Sharpness-Aware Minimization (SAM) [1] 是一种用于寻找更平坦极值点的技术,被认为是当前最有前途的技术方向之一。SAM技术被广泛应用于计算机视觉、自然语言处理和双层学习等多个领域,并在这些领域中明显优于之前的最先进方法
为了探索更平坦的最小值,SAM 定义损失函数 L 在 w 处的平坦程度如下:
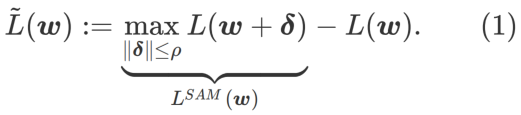
GSAM [2] 证明了 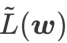 是局部极值点 Hessian 矩阵最大特征值的近似,表明
是局部极值点 Hessian 矩阵最大特征值的近似,表明 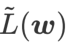 确实是平坦(陡峭)程度的有效度量。然而
确实是平坦(陡峭)程度的有效度量。然而 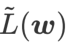 只能用于寻找更平坦的区域而不是最小值点,这可能导致损失函数收敛到损失值依然很大的点(虽然周围区域很平坦)。因此,SAM 采用
只能用于寻找更平坦的区域而不是最小值点,这可能导致损失函数收敛到损失值依然很大的点(虽然周围区域很平坦)。因此,SAM 采用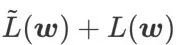 ,即
,即 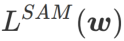 作为损失函数。它可以视为在
作为损失函数。它可以视为在 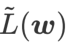 和
和 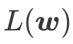 之间寻找更平坦的表面和更小损失值的折衷方案,在这里两者被赋予了同等的权重。
之间寻找更平坦的表面和更小损失值的折衷方案,在这里两者被赋予了同等的权重。
本文重新思考了 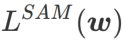 的构建,将
的构建,将 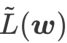 视为正则化项。我们开发了一个更通用、有效的算法,称为 WSAM(Weighted Sharpness-Aware Minimization),其损失函数加入了一个加权平坦度项
视为正则化项。我们开发了一个更通用、有效的算法,称为 WSAM(Weighted Sharpness-Aware Minimization),其损失函数加入了一个加权平坦度项 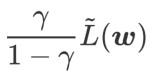 作为正则项,其中超参数
作为正则项,其中超参数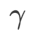 控制了平坦度的权重。在方法介绍章节,我们演示了如何通过
控制了平坦度的权重。在方法介绍章节,我们演示了如何通过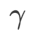 来指导损失函数找到更平坦或更小的极值点。我们的关键贡献可以总结如下。
来指导损失函数找到更平坦或更小的极值点。我们的关键贡献可以总结如下。
- 我们提出 WSAM,将平坦度视为正则化项,并在不同任务之间给予不同的权重。我们提出一个“权重解耦”技术来处理更新公式中的正则化项,旨在精确反映当前步骤的平坦度。当基础优化器不是 SGD 时,如 SGDM 和 Adam,WSAM 在形式上与 SAM 有显著差异。消融实验表明,这种技术在大多数情况下可以提升效果。
- 我们在公开数据集上验证了 WSAM 在常见任务中的有效性。实验结果表明,与 SAM 及其变体相比,WSAM 在绝大多数情形都有着更好的泛化性能。
预备知识
SAM 是解决由公式(1)定义的 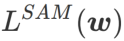 的极小极大最优化问题的一种技术。
的极小极大最优化问题的一种技术。
首先,SAM 使用围绕 w 的一阶泰勒展开来近似内层的最大化问题,即、
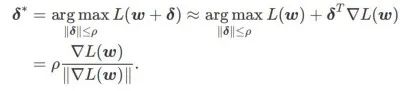
其次,SAM 通过采用 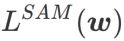 的近似梯度来更新 w ,即
的近似梯度来更新 w ,即
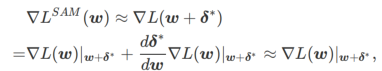
其中第二个近似是为了加速计算。其他基于梯度的优化器(称为基础优化器)可以纳入 SAM 的通用框架中,具体见Algorithm 1。通过改变 Algorithm 1 中的 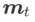 和
和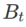 ,我们可以获得不同的基础优化器,例如 SGD、SGDM 和 Adam,参见 Tab. 1。请注意,当基础优化器为 SGD 时,Algorithm 1 回退到 SAM 论文 [1] 中的原始 SAM。
,我们可以获得不同的基础优化器,例如 SGD、SGDM 和 Adam,参见 Tab. 1。请注意,当基础优化器为 SGD 时,Algorithm 1 回退到 SAM 论文 [1] 中的原始 SAM。


方法介绍
WSAM 的设计细节
在此,我们给出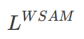 的正式定义,它由一个常规损失和一个平坦度项组成。由公式(1),我们有
的正式定义,它由一个常规损失和一个平坦度项组成。由公式(1),我们有
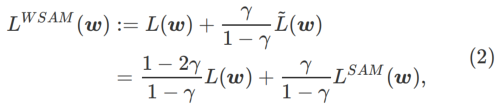
其中 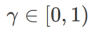 。當
。當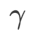 =0 時,
=0 時,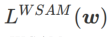 退化為常規損失;當
退化為常規損失;當 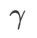 =1/2 時,
=1/2 時,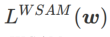 等價於
等價於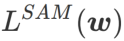 ;當
;當 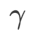 >1/2 時,
>1/2 時,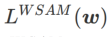 更重視平坦度,因此與SAM 相比更容易找到較小曲率而非較小損失值的點;反之亦然亦然。
更重視平坦度,因此與SAM 相比更容易找到較小曲率而非較小損失值的點;反之亦然亦然。
包含不同基本最佳化器的WSAM 的一般框架可以透過選擇不同的 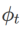 和
和 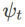 來實現,請參閱Algorithm 2。例如,當
來實現,請參閱Algorithm 2。例如,當  和
和 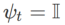 時,我們得到基礎最佳化器為 SGD 的 WSAM,請參閱 Algorithm 3。在此,我們採用了一種「權重解耦」技術,即
時,我們得到基礎最佳化器為 SGD 的 WSAM,請參閱 Algorithm 3。在此,我們採用了一種「權重解耦」技術,即 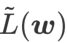 平坦度項不是與基礎最佳化器整合用於計算梯度和更新權重,而是獨立計算(Algorithm 2 第7 行的最後一項)。這樣,正則化的效果只反映了當前步驟的平坦度,而沒有額外的資訊。為了進行比較,Algorithm 4 給出了沒有「權重解耦」(稱為 Coupled-WSAM)的 WSAM。例如,如果基本最佳化器是 SGDM,則 Coupled-WSAM 的正規化項是平坦度的指數移動平均值。如實驗章節所示,「權重解耦」可以在大多數情況下改善泛化表現。
平坦度項不是與基礎最佳化器整合用於計算梯度和更新權重,而是獨立計算(Algorithm 2 第7 行的最後一項)。這樣,正則化的效果只反映了當前步驟的平坦度,而沒有額外的資訊。為了進行比較,Algorithm 4 給出了沒有「權重解耦」(稱為 Coupled-WSAM)的 WSAM。例如,如果基本最佳化器是 SGDM,則 Coupled-WSAM 的正規化項是平坦度的指數移動平均值。如實驗章節所示,「權重解耦」可以在大多數情況下改善泛化表現。




Fig. 1 展示了不同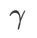 取值下的 WSAM 更新過程。當
取值下的 WSAM 更新過程。當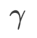 時,
時,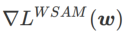 介於
介於 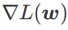 與
與 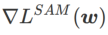 之間,並隨著
之間,並隨著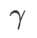 增大逐漸偏離
增大逐漸偏離 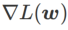 。
。

簡單範例
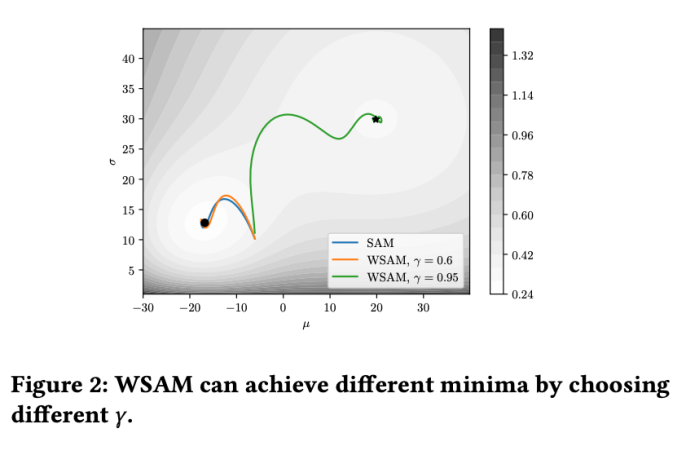
#為了更好說明WSAM 中 γ 的效果和優勢,我們設定了一個二維簡單範例。如Fig. 2 所示,損失函數在左下角有一個相對不平坦的極值點(位置:(-16.8, 12.8),損失值:0.28),在右上角有一個平坦的極值點(位置: (19.8, 29.9),損失值:0.36)。損失函數定義為: 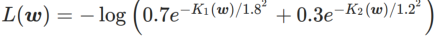 ,這裡
,這裡 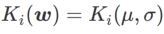 是單變量高斯模型與兩個常態分佈之間的KL 散度,即
是單變量高斯模型與兩個常態分佈之間的KL 散度,即 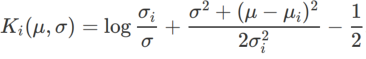 # ,其中
# ,其中 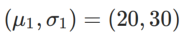 和
和 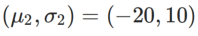 # 。
# 。
我們使用動量為 0.9 的 SGDM 作為基本最佳化器,並對 SAM 和 WSAM 設定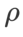 =2 。從初始點 (-6, 10) 開始,使用學習率為 5 在 150 步驟內最佳化損失函數。 SAM 收斂到損失值較低但較不平坦的極值點,
=2 。從初始點 (-6, 10) 開始,使用學習率為 5 在 150 步驟內最佳化損失函數。 SAM 收斂到損失值較低但較不平坦的極值點,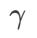 =0.6的 WSAM 也類似。然而,
=0.6的 WSAM 也類似。然而,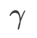 =0.95 使得損失函數收斂到平坦的極值點,顯示更強的平坦度正規化發揮了作用。
=0.95 使得損失函數收斂到平坦的極值點,顯示更強的平坦度正規化發揮了作用。
實驗
#我們在各種任務上進行了實驗,以驗證WSAM 的有效性。
影像分類
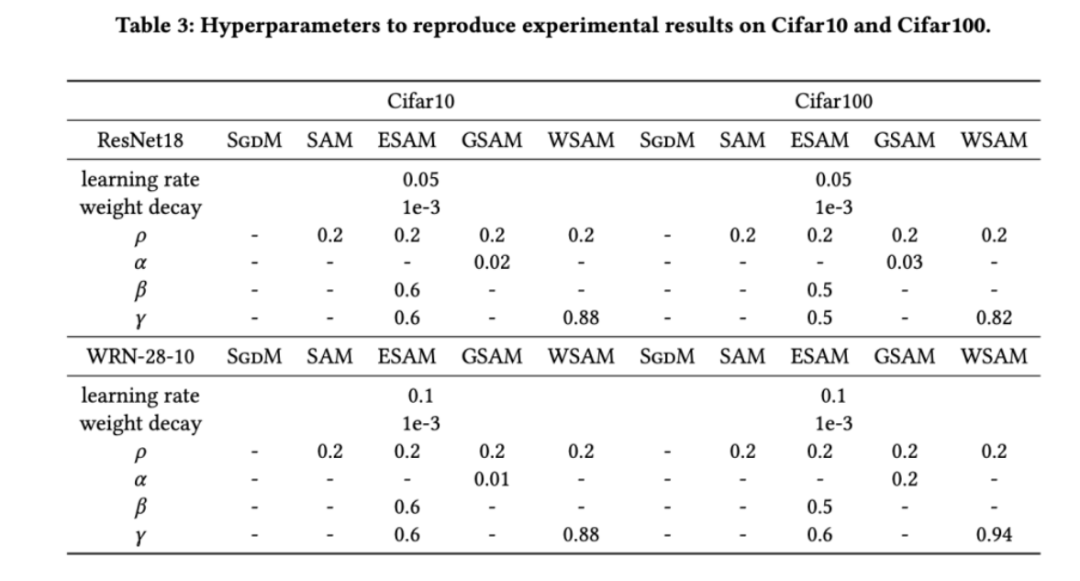
我們首先研究了 WSAM 在 Cifar10 和 Cifar100 資料集上從零開始訓練模型的效果。我們選擇的模型包括 ResNet18 和WideResNet-28-10。我們使用預先定義的批次大小在 Cifar10 和 Cifar100 上訓練模型,ResNet18 和 WideResNet-28-10 分別為 128,256。這裡使用的基礎優化器是動量為 0.9 的 SGDM。依照 SAM [1] 的設置,每個基礎優化器跑的 epoch 數是 SAM 類優化器的兩倍。我們對兩個模型都進行了 400 個 epoch 的訓練(SAM 類優化器為 200 個 epoch),並使用 cosine scheduler 來衰減學習率。這裡我們沒有使用其他進階資料增強方法,例如 cutout 和 AutoAugment。
對於兩個模型,我們使用聯合網格搜尋確定基礎最佳化器的學習率和權重衰減係數,並將它們保持不變用於接下來的 SAM 類別最佳化器實驗。學習率和權重衰減係數的搜尋範圍分別為 {0.05, 0.1} 和 {1e-4, 5e-4, 1e-3}。由於所有SAM 類別優化器都有一個超參數 (鄰域大小),我們接下來在SAM 優化器上搜尋最佳的
(鄰域大小),我們接下來在SAM 優化器上搜尋最佳的 並將相同的值用於其他SAM類別優化器。
並將相同的值用於其他SAM類別優化器。  的搜尋範圍為 {0.01, 0.02, 0.05, 0.1, 0.2, 0.5}。最後,我們對其他 SAM 類優化器各自獨有的超參進行搜索,搜索範圍來自各自原始文章的建議範圍。對於 GSAM [2],我們在 {0.01, 0.02, 0.03, 0.1, 0.2, 0.3} 範圍內搜尋。對於 ESAM [3],我們在{0.4, 0.5, 0.6} 範圍內搜尋
的搜尋範圍為 {0.01, 0.02, 0.05, 0.1, 0.2, 0.5}。最後,我們對其他 SAM 類優化器各自獨有的超參進行搜索,搜索範圍來自各自原始文章的建議範圍。對於 GSAM [2],我們在 {0.01, 0.02, 0.03, 0.1, 0.2, 0.3} 範圍內搜尋。對於 ESAM [3],我們在{0.4, 0.5, 0.6} 範圍內搜尋  ,在{0.4, 0.5, 0.6} 範圍內搜尋
,在{0.4, 0.5, 0.6} 範圍內搜尋 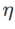 ,在{0.4, 0.5, 0.6} 範圍內搜尋
,在{0.4, 0.5, 0.6} 範圍內搜尋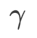 。對於 WSAM,我們在 {0.5, 0.6, 0.7, 0.8, 0.82, 0.84, 0.86, 0.88, 0.9, 0.92, 0.94, 0.96} 範圍內搜尋
。對於 WSAM,我們在 {0.5, 0.6, 0.7, 0.8, 0.82, 0.84, 0.86, 0.88, 0.9, 0.92, 0.94, 0.96} 範圍內搜尋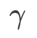 。我們使用不同的隨機種子重複實驗 5 次,計算了平均誤差和標準差。我們在單卡 NVIDIA A100 GPU 上進行實驗。每個模型的優化器超參總結在 Tab. 3 中。
。我們使用不同的隨機種子重複實驗 5 次,計算了平均誤差和標準差。我們在單卡 NVIDIA A100 GPU 上進行實驗。每個模型的優化器超參總結在 Tab. 3 中。
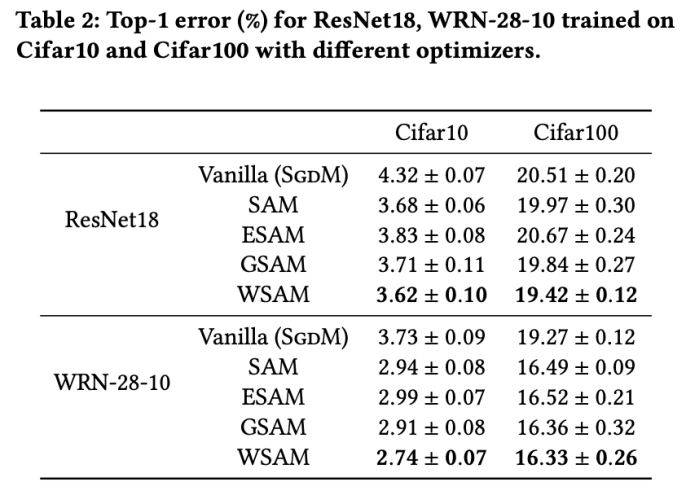
Tab. 2 給出了在不同優化器下,ResNet18、WRN-28-10 在Cifar10 和Cifar100 上測試集的top- 1 錯誤率。相較於基礎優化器,SAM 類優化器顯著提升了效果,同時,WSAM 又顯著優於其他 SAM 類優化器。
ImageNet 上的額外訓練
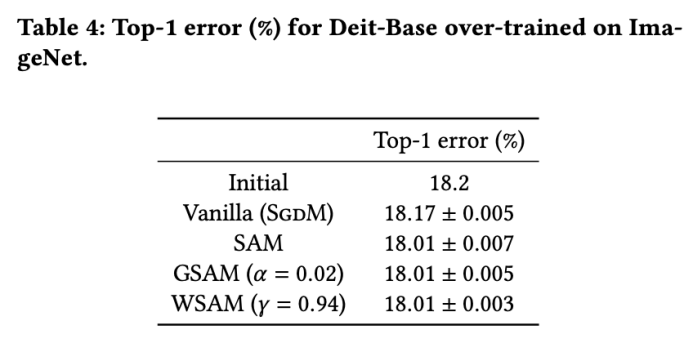
我們在ImageNet資料集上進一步使用Data-Efficient Image Transformers網路架構進行實驗。我們恢復了一個預先訓練的DeiT-base檢查點,然後繼續訓練三個epoch。模型使用批次大小256進行訓練,基礎優化器為動量0.9的SGDM,權重衰減係數為1e-4,學習率為1e-5。我們在四卡NVIDIA A100 GPU重複運行5次,併計算平均誤差和標準差
我們在 {0.05, 0.1, 0.5, 1.0,⋯ , 6.0} 中搜尋SAM的最佳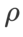 。最佳的
。最佳的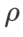 =5.5 直接用於其他 SAM 類別最佳化器。之後,我們在{0.01, 0.02, 0.03, 0.1, 0.2, 0.3}中搜尋GSAM 的最佳
=5.5 直接用於其他 SAM 類別最佳化器。之後,我們在{0.01, 0.02, 0.03, 0.1, 0.2, 0.3}中搜尋GSAM 的最佳  ,並在0.80 到0.98 之間以0.02 的步長搜尋WSAM 的最佳
,並在0.80 到0.98 之間以0.02 的步長搜尋WSAM 的最佳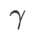 。
。
模型的初始 top-1 錯誤率為 18.2%,在進行了三個額外的 epoch 之後,錯誤率如 Tab. 4 所示。我們沒有發現三個 SAM-like 優化器之間有明顯的差異,但它們都優於基礎優化器,表明它們可以找到更平坦的極值點並具有更好的泛化能力。
標籤雜訊的穩健性
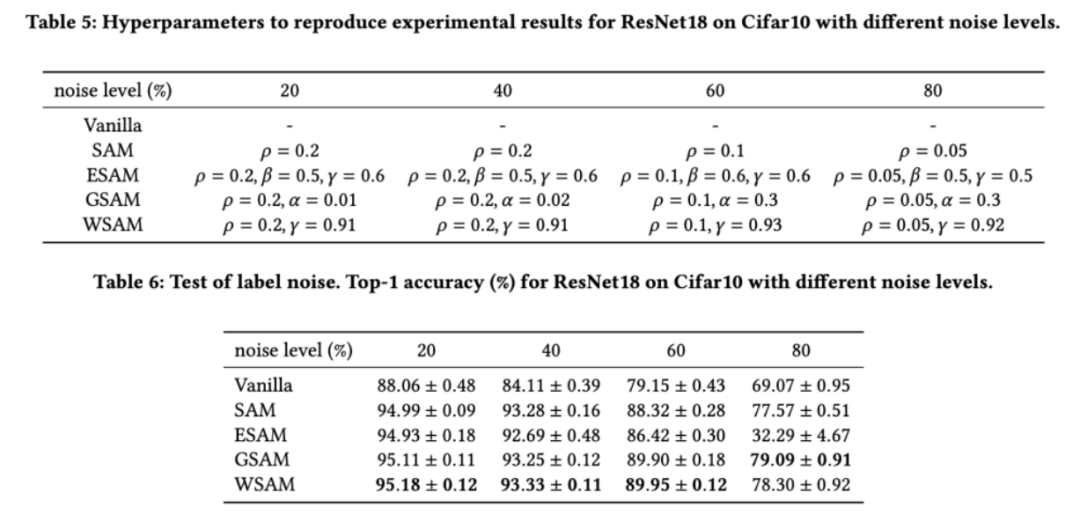
如先前的研究[1, 4, 5] 所示,SAM 類別最佳化器在訓練集存在標籤雜訊時表現出良好的魯棒性。在這裡,我們將 WSAM 的穩健性與 SAM、ESAM 和 GSAM 進行了比較。我們在 Cifar10 資料集上訓練 ResNet18 200 個 epoch,並注入對稱標籤噪聲,噪聲水準為 20%、40%、60% 和 80%。我們使用具有 0.9 動量的 SGDM 作為基礎優化器,批次大小為 128,學習率為 0.05,權重衰減係數為 1e-3,並使用 cosine scheduler 衰減學習率。針對每個標籤雜訊水平,我們在 {0.01, 0.02, 0.05, 0.1, 0.2, 0.5} 範圍內對 SAM 進行網格搜索,確定通用的 值。然後,我們單獨搜尋其他優化器特定的超參數,以找到最優泛化效能。我們在 Tab. 5 中列出了復現我們結果所需的超參數。我們在 Tab. 6 中給出了穩健性測試的結果,WSAM 通常比 SAM、ESAM 和 GSAM 都具有更好的穩健性。
值。然後,我們單獨搜尋其他優化器特定的超參數,以找到最優泛化效能。我們在 Tab. 5 中列出了復現我們結果所需的超參數。我們在 Tab. 6 中給出了穩健性測試的結果,WSAM 通常比 SAM、ESAM 和 GSAM 都具有更好的穩健性。
探索幾何的影響
SAM 類別最佳化器可以與ASAM [4] 和Fisher SAM [5] 等技術結合,以自適應地調整探索鄰域的形狀。我們在 Cifar10 上對 WRN-28-10 進行實驗,比較 SAM 和 WSAM 在分別使用自適應和 Fisher 資訊方法時的表現,以了解探索區域的幾何結構如何影響 SAM 類優化器的泛化性能。
除了 和
和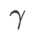 之外的參數,我們重複使用了影像分類中的配置。根據先前的研究 [4, 5],ASAM 和 Fisher SAM 的
之外的參數,我們重複使用了影像分類中的配置。根據先前的研究 [4, 5],ASAM 和 Fisher SAM 的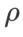 通常較大。我們在 {0.1, 0.5, 1.0,…, 6.0} 中搜尋最佳的
通常較大。我們在 {0.1, 0.5, 1.0,…, 6.0} 中搜尋最佳的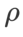 ,ASAM 和 Fisher SAM 最佳的
,ASAM 和 Fisher SAM 最佳的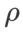 #都是 5.0。之後,我們在 0.80 到 0.94 之間以 0.02 的步長搜尋 WSAM 的最佳
#都是 5.0。之後,我們在 0.80 到 0.94 之間以 0.02 的步長搜尋 WSAM 的最佳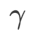 ,兩種方法最佳
,兩種方法最佳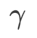 都是 0.88。
都是 0.88。
令人驚訝的是,如 Tab. 7 所示,即使在多個候選項中,基準的 WSAM 也表現出更好的泛化性。因此,我們建議直接使用具有固定的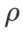 基準 WSAM 即可。
基準 WSAM 即可。

消融實驗
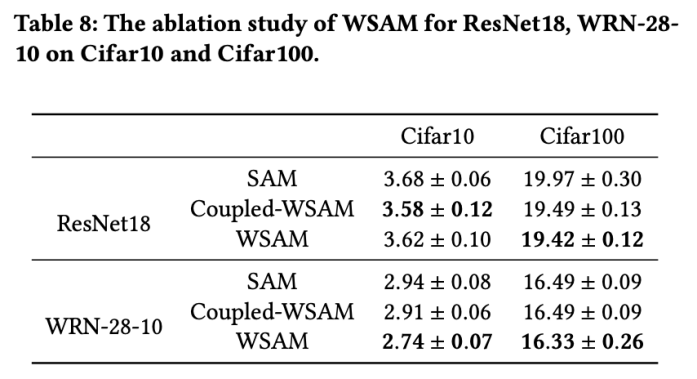
#在本節中,我們進行消融實驗,以深入理解WSAM 中“權重解耦”技術的重要性。如WSAM 的設計細節所述,我們將不含「權重解耦」的 WSAM 變體(演算法 4)Coupled-WSAM 與原始方法進行比較。
結果如 Tab. 8 所示。 Coupled-WSAM 在大多數情況下比 SAM 產生更好的結果,WSAM 在大多數情況下進一步提升了效果,證明「權重解耦」技術的有效性。
極值點分析
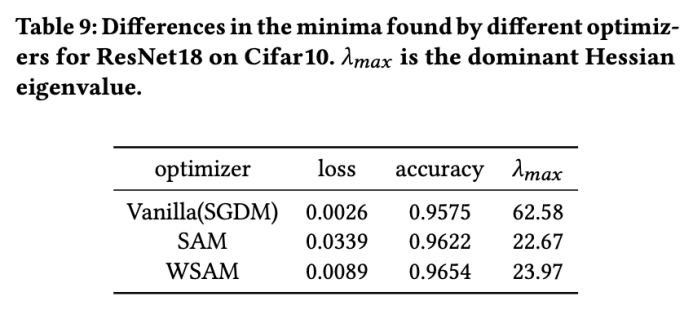
在這裡,我們透過比較WSAM 和SAM 最佳化器找到的極值點之間的差異,進一步加深對WSAM 優化器的理解。極值點處的平坦(陡峭)度可透過 Hessian 矩陣的最大特徵值來描述。特徵值越大,越不平坦。我們使用 Power Iteration 演算法來計算這個最大特徵值。
Tab. 9 顯示了 SAM 和 WSAM 最佳化器找到的極值點之間的差異。我們發現,vanilla 最佳化器找到的極值點具有較小的損失值但較不平坦,而 SAM 找到的極值點具有較大的損失值但較平坦,從而改善了泛化效能。有趣的是,WSAM 找到的極值點不僅損失值比 SAM 小得多,而且平坦度十分接近 SAM。這表明,在尋找極端值點的過程中,WSAM 優先確保較小的損失值,同時盡量搜尋到更平坦的區域。
超參敏感性
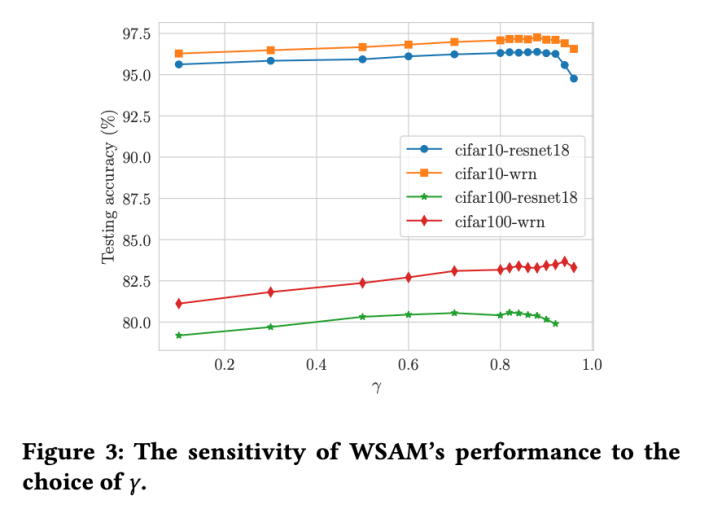
#與SAM 相比,WSAM 具有額外的超參數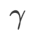 ,用於縮放平坦(陡峭)度項的大小。在這裡,我們測試 WSAM 的泛化性能對該超參的敏感度。我們在 Cifar10 和 Cifar100 上使用 WSAM 對 ResNet18 和 WRN-28-10 模型進行了訓練,使用了廣泛的
,用於縮放平坦(陡峭)度項的大小。在這裡,我們測試 WSAM 的泛化性能對該超參的敏感度。我們在 Cifar10 和 Cifar100 上使用 WSAM 對 ResNet18 和 WRN-28-10 模型進行了訓練,使用了廣泛的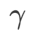 取值。如 Fig. 3 所示,結果顯示 WSAM 對超參
取值。如 Fig. 3 所示,結果顯示 WSAM 對超參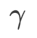 的選擇不敏感。我們還發現,WSAM 的最優泛化效能幾乎總是在 0.8 到 0.95 之間。
的選擇不敏感。我們還發現,WSAM 的最優泛化效能幾乎總是在 0.8 到 0.95 之間。
以上是更通用、有效,螞蟻自研優化器WSAM入選KDD Oral的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

AI Hentai Generator
免費產生 AI 無盡。

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)

熱門話題
 使用ddrescue在Linux上恢復數據
Mar 20, 2024 pm 01:37 PM
使用ddrescue在Linux上恢復數據
Mar 20, 2024 pm 01:37 PM
DDREASE是一種用於從檔案或區塊裝置(如硬碟、SSD、RAM磁碟、CD、DVD和USB儲存裝置)復原資料的工具。它將資料從一個區塊設備複製到另一個區塊設備,留下損壞的資料區塊,只移動好的資料區塊。 ddreasue是一種強大的恢復工具,完全自動化,因為它在恢復操作期間不需要任何干擾。此外,由於有了ddasue地圖文件,它可以隨時停止和恢復。 DDREASE的其他主要功能如下:它不會覆寫恢復的數據,但會在迭代恢復的情況下填補空白。但是,如果指示工具明確執行此操作,則可以將其截斷。將資料從多個檔案或區塊還原到單
 開源!超越ZoeDepth! DepthFM:快速且精確的單目深度估計!
Apr 03, 2024 pm 12:04 PM
開源!超越ZoeDepth! DepthFM:快速且精確的單目深度估計!
Apr 03, 2024 pm 12:04 PM
0.這篇文章乾了啥?提出了DepthFM:一個多功能且快速的最先進的生成式單目深度估計模型。除了傳統的深度估計任務外,DepthFM還展示了在深度修復等下游任務中的最先進能力。 DepthFM效率高,可以在少數推理步驟內合成深度圖。以下一起來閱讀這項工作~1.論文資訊標題:DepthFM:FastMonocularDepthEstimationwithFlowMatching作者:MingGui,JohannesS.Fischer,UlrichPrestel,PingchuanMa,Dmytr
 你好,電動Atlas!波士頓動力機器人復活,180度詭異動作嚇到馬斯克
Apr 18, 2024 pm 07:58 PM
你好,電動Atlas!波士頓動力機器人復活,180度詭異動作嚇到馬斯克
Apr 18, 2024 pm 07:58 PM
波士頓動力Atlas,正式進入電動機器人時代!昨天,液壓Atlas剛「含淚」退出歷史舞台,今天波士頓動力就宣布:電動Atlas上崗。看來,在商用人形機器人領域,波士頓動力是下定決心要跟特斯拉硬剛一把了。新影片放出後,短短十幾小時內,就已經有一百多萬觀看。舊人離去,新角色登場,這是歷史的必然。毫無疑問,今年是人形機器人的爆發年。網友銳評:機器人的進步,讓今年看起來像人類的開幕式動作、自由度遠超人類,但這真不是恐怖片?影片一開始,Atlas平靜地躺在地上,看起來應該是仰面朝天。接下來,讓人驚掉下巴
 Google狂喜:JAX性能超越Pytorch、TensorFlow!或成GPU推理訓練最快選擇
Apr 01, 2024 pm 07:46 PM
Google狂喜:JAX性能超越Pytorch、TensorFlow!或成GPU推理訓練最快選擇
Apr 01, 2024 pm 07:46 PM
谷歌力推的JAX在最近的基準測試中表現已經超過Pytorch和TensorFlow,7項指標排名第一。而且測試並不是JAX性能表現最好的TPU上完成的。雖然現在在開發者中,Pytorch依然比Tensorflow更受歡迎。但未來,也許有更多的大型模型會基於JAX平台進行訓練和運行。模型最近,Keras團隊為三個後端(TensorFlow、JAX、PyTorch)與原生PyTorch實作以及搭配TensorFlow的Keras2進行了基準測試。首先,他們為生成式和非生成式人工智慧任務選擇了一組主流
 iPhone上的蜂窩數據網路速度慢:修復
May 03, 2024 pm 09:01 PM
iPhone上的蜂窩數據網路速度慢:修復
May 03, 2024 pm 09:01 PM
在iPhone上面臨滯後,緩慢的行動數據連線?通常,手機上蜂窩互聯網的強度取決於幾個因素,例如區域、蜂窩網絡類型、漫遊類型等。您可以採取一些措施來獲得更快、更可靠的蜂窩網路連線。修復1–強制重啟iPhone有時,強制重啟設備只會重置許多內容,包括蜂窩網路連線。步驟1–只需按一次音量調高鍵並放開即可。接下來,按降低音量鍵並再次釋放它。步驟2–過程的下一部分是按住右側的按鈕。讓iPhone完成重啟。啟用蜂窩數據並檢查網路速度。再次檢查修復2–更改資料模式雖然5G提供了更好的網路速度,但在訊號較弱
 快手版Sora「可靈」開放測試:生成超120s視頻,更懂物理,複雜運動也能精準建模
Jun 11, 2024 am 09:51 AM
快手版Sora「可靈」開放測試:生成超120s視頻,更懂物理,複雜運動也能精準建模
Jun 11, 2024 am 09:51 AM
什麼?瘋狂動物城被國產AI搬進現實了?與影片一同曝光的,是一款名為「可靈」全新國產影片生成大模型。 Sora利用了相似的技術路線,結合多項自研技術創新,生產的影片不僅運動幅度大且合理,還能模擬物理世界特性,具備強大的概念組合能力與想像。數據上看,可靈支持生成長達2分鐘的30fps的超長視頻,分辨率高達1080p,且支援多種寬高比。另外再劃個重點,可靈不是實驗室放出的Demo或影片結果演示,而是短影片領域頭部玩家快手推出的產品級應用。而且主打一個務實,不開空頭支票、發布即上線,可靈大模型已在快影
 超級智能體生命力覺醒!可自我更新的AI來了,媽媽再也不用擔心資料瓶頸難題
Apr 29, 2024 pm 06:55 PM
超級智能體生命力覺醒!可自我更新的AI來了,媽媽再也不用擔心資料瓶頸難題
Apr 29, 2024 pm 06:55 PM
哭死啊,全球狂煉大模型,一網路的資料不夠用,根本不夠用。訓練模型搞得跟《飢餓遊戲》似的,全球AI研究者,都在苦惱怎麼才能餵飽這群資料大胃王。尤其在多模態任務中,這問題尤其突出。一籌莫展之際,來自人大系的初創團隊,用自家的新模型,率先在國內把「模型生成數據自己餵自己」變成了現實。而且還是理解側和生成側雙管齊下,兩側都能產生高品質、多模態的新數據,對模型本身進行數據反哺。模型是啥?中關村論壇上剛露面的多模態大模型Awaker1.0。團隊是誰?智子引擎。由人大高瓴人工智慧學院博士生高一鑷創立,高
 美國空軍高調展示首個AI戰鬥機!部長親自試駕全程未乾預,10萬行代碼試飛21次
May 07, 2024 pm 05:00 PM
美國空軍高調展示首個AI戰鬥機!部長親自試駕全程未乾預,10萬行代碼試飛21次
May 07, 2024 pm 05:00 PM
最近,軍事圈被這個消息刷屏了:美軍的戰鬥機,已經能由AI完成全自動空戰了。是的,就在最近,美軍的AI戰鬥機首次公開,揭開了神秘面紗。這架戰鬥機的全名是可變穩定性飛行模擬器測試飛機(VISTA),由美空軍部長親自搭乘,模擬了一對一的空戰。 5月2日,美國空軍部長FrankKendall在Edwards空軍基地駕駛X-62AVISTA升空注意,在一小時的飛行中,所有飛行動作都由AI自主完成! Kendall表示——在過去的幾十年中,我們一直在思考自主空對空作戰的無限潛力,但它始終顯得遙不可及。然而如今,






