陶哲軒再逼近60年幾何學難題!週期性密鋪問題又獲新突破
陶哲軒在研究週期性密鋪問題時取得了新的突破
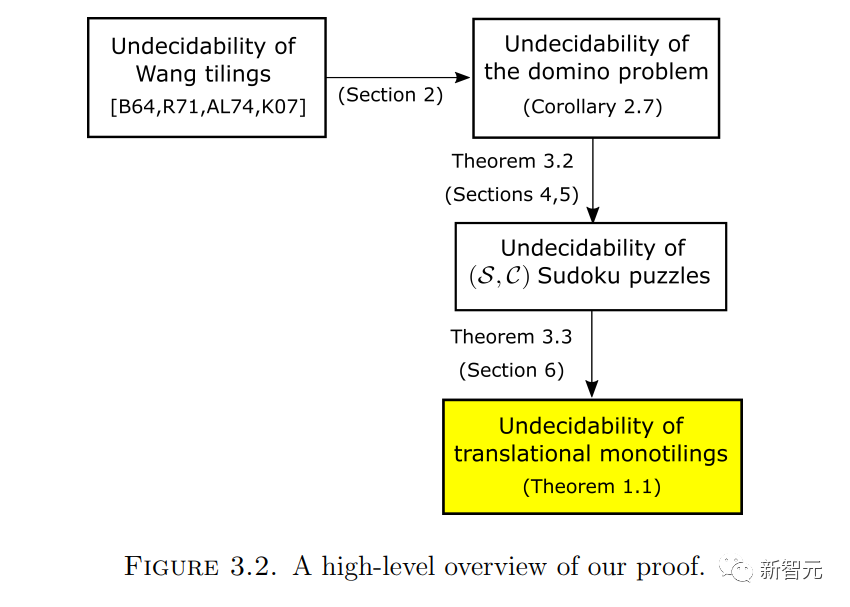
9月18日,陶哲軒和Rachel Greenfeld將預印本論文《平移單密舖的不可判定性(Undecidability of translational monotilings)》上傳到了arXiv。

論文網址:https://arxiv.org/abs/2309.09504
這篇論文的主要結論是,如果網格的維度是無界的,那麼確定網格的有限子集是否可以平鋪該網格的周期子集的問題,就是不可判定的
#要知道,此問題在維度1和維度2中是可判定的。
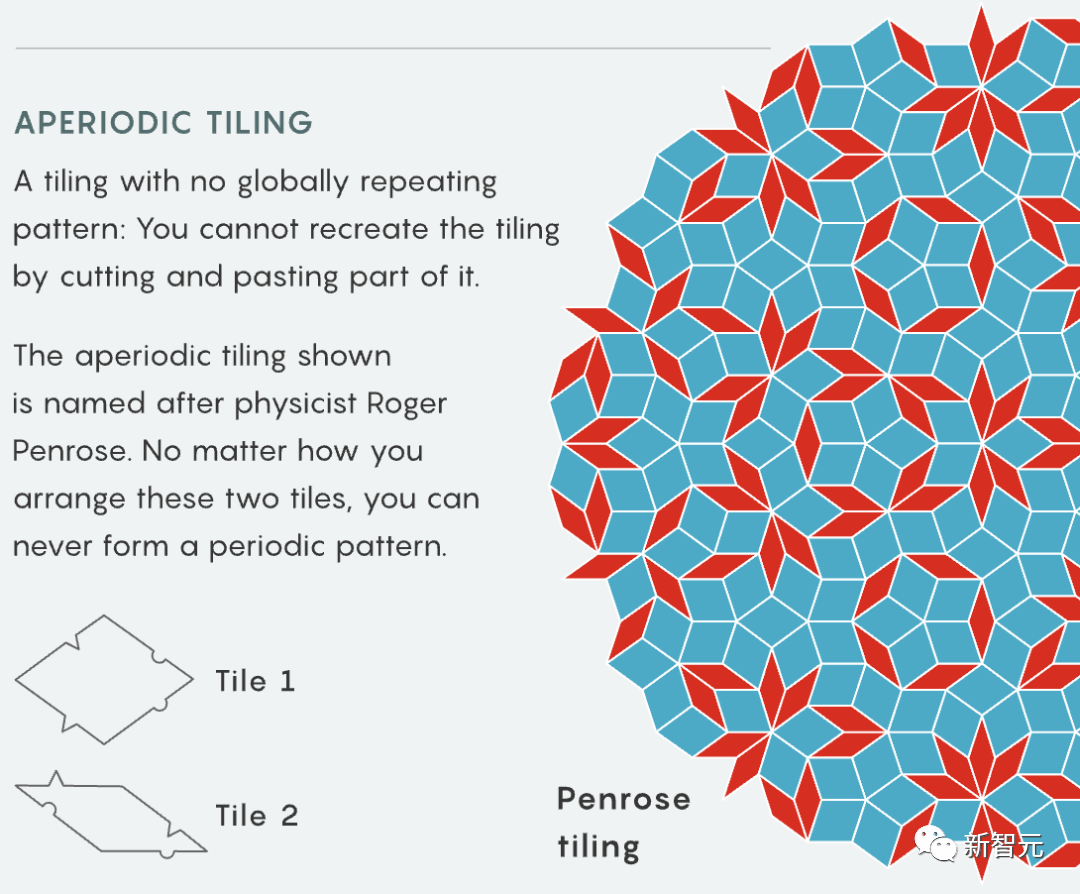
陶哲軒表示,有點奇怪的是,文中所證明的大多數組件都與流行的遊戲類似——
骨牌的密鋪類似物,數獨,電腦遊戲“俄羅斯方塊”,甚至連兒童遊戲“Fizz buzz”都有出現
為什麼研究一個數學問題會牽扯到這麼多遊戲呢?陶哲軒也無法解釋

#平移單密舖的不可判定性
這次的論文,是兩人上一篇論文的續集。連結 週期性密鋪問題
在上篇論文中,他們建構了一個高維度網格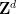 #的平移單密舖
#的平移單密舖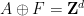
(因此單密舖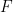 是一個有限集合),它是非週期性的(沒有辦法將這個密舖「修復」成週期性密舖
是一個有限集合),它是非週期性的(沒有辦法將這個密舖「修復」成週期性密舖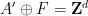 ,其中
,其中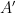 現在相對於有限索引子群組
現在相對於有限索引子群組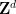 #是周期性的)。
#是周期性的)。

這一事實否定了Stein、Grunbaum-Shephard和Lagarias-Wang關於非週期性密舖單體不存在的假設
(「帽子單舖」是一種最近發現的非週期等距單密舖 ,在這種單密舖中,可以允許使用旋轉、反射以及平移,或更新的「幽靈單片」。上述單片與帽子單密鋪相似,除了不需要反射)。
,在這種單密舖中,可以允許使用旋轉、反射以及平移,或更新的「幽靈單片」。上述單片與帽子單密鋪相似,除了不需要反射)。
陶哲軒和Rachel Greenfeld激發這個猜想的原因之一,是數學家Hao Wang的觀察

他發現,如果週期密鋪猜想為真,那麼平移密鋪問題在演算法上是可判定的-
有一個圖靈機,對於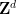 ,當給定一個維度
,當給定一個維度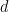 和一個有限子集
和一個有限子集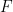 時,可以在有限的時間內確定
時,可以在有限的時間內確定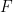 是否可以密舖
是否可以密舖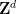 #。
#。
這是由於如果存在周期性的密舖,就可以透過電腦搜尋來找到它
如果根本不存在密舖,那麼透過緊緻性定理可知,存在一些有限的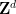 子集,這些子集不能被
子集,這些子集不能被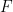 不相交的平移所覆蓋,這也可以透過計算機搜尋來發現。
不相交的平移所覆蓋,這也可以透過計算機搜尋來發現。
週期性密鋪猜想斷言這是僅有的兩種可能的情況,從而給出了可判定性。

另一方面,王的觀點是不可改變的:週期性密舖猜想的失敗,並不自動意味著平移單密舖問題的不可判定性,因為它並不排除存在其他演算法來確定密鋪,這種密舖可以不依賴週期性密舖的存在
(例如,即使有新發現的帽子和幽靈密鋪,對於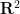 中有理係數的多邊形的等距單密舖問題是否是可判定的,仍然是一個懸而未決的問題,無論它有沒有反射。
中有理係數的多邊形的等距單密舖問題是否是可判定的,仍然是一個懸而未決的問題,無論它有沒有反射。
本文的主要結果解決了這個問題(有一個警告):

需要重寫的內容是:定理1
不存在任何演算法,對於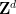 ,給定一個維度
,給定一個維度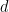 ,一個週期性子集
,一個週期性子集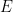 ,和一個有限子集
,和一個有限子集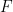 #,能在有限時間內確定是否存在一個平移密舖
#,能在有限時間內確定是否存在一個平移密舖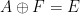 #。
#。
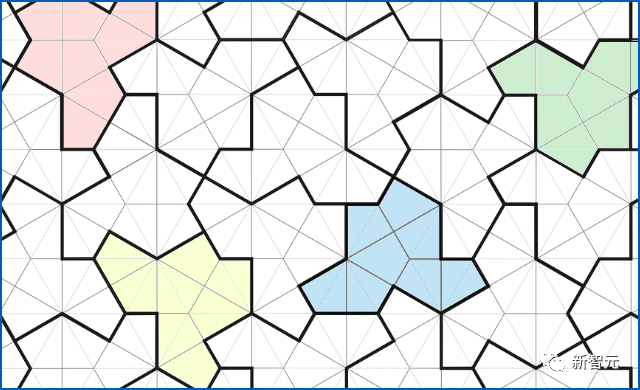
要注意的是,必須使用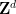 的周期性子集
的周期性子集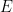 #,而不是全部的
#,而不是全部的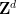 ;這在很大程度上是由於這種方法的技術限制,並且很可能透過額外的努力和創造力來消除。
;這在很大程度上是由於這種方法的技術限制,並且很可能透過額外的努力和創造力來消除。
另外,陶哲軒和Rachel Greenfeld也注意到,當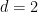 ,週期性密鋪猜想是由Bhattacharya建立的,因此在
,週期性密鋪猜想是由Bhattacharya建立的,因此在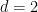 這種情況下問題可判定。
這種情況下問題可判定。
對於任何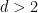 的固定值,密舖問題是否可判定仍然是開放的(注意,在上面的結果中,維度
的固定值,密舖問題是否可判定仍然是開放的(注意,在上面的結果中,維度 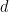 不是固定的,而是輸入的一部分)。
不是固定的,而是輸入的一部分)。
由於演算法不可判定性和邏輯不可判定性(也稱為邏輯獨立性)之間存在眾所周知的聯繫,此定理還暗示了存在一個(原則上明確可描述的)維度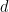 、
、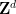 #的周期性子集
#的周期性子集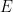 ,
,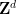 的有限子集
的有限子集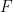 ,使得
,使得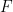 能透過平移密舖
能透過平移密舖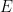 不能在ZFC集合論中被證實或證偽(當然假設這個理論是一致的)。
不能在ZFC集合論中被證實或證偽(當然假設這個理論是一致的)。
作為這種方法的結果,我們也可以在這裡用「幾乎是二維」群組 來取代
來取代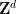 #,其中
#,其中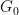 是一個有限阿貝爾群組(現在成為輸入的一部分,代替維度
是一個有限阿貝爾群組(現在成為輸入的一部分,代替維度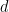 )。
)。
接下來,描述證明的一些主要想法。
證明某個問題不可判定的常用方法是,將已知不可判定的其他問題「編碼」到原始問題中,這樣,任何判定原始問題的演算法也能判定嵌入的問題
因此,我們將Wang密舖問題編碼為單密舖問題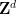 :
:

##第二個問題是關於王密舖問題
給定一個有限的王氏密鋪集合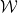 (單位正方形,每條邊都從有限調色板中指定了某種顏色),是否有可能用標準的格
(單位正方形,每條邊都從有限調色板中指定了某種顏色),是否有可能用標準的格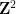 通過平移來密鋪平面,使得相鄰的密舖在共同邊緣上具有相同的顏色?
通過平移來密鋪平面,使得相鄰的密舖在共同邊緣上具有相同的顏色?
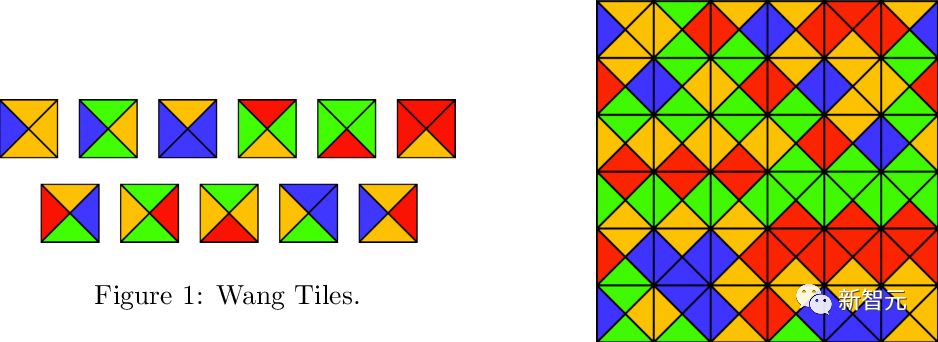
Berger曾經提出了一個著名的結論,即這個問題無法確定

需要重寫的內容是:Berger,Robert,
#將這個問題轉化為高維度平移單密鋪問題需要解決一些中間問題
首先,我們可以很容易地將王氏密舖問題嵌入到一個類似的問題中,我們稱之為多米諾骨牌問題:

重寫內容如下:骨牌問題是問題3
給定一個水平(或垂直)的骨牌的有限集合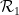 或
或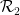 ,它們是一對相鄰的單元正方形,每個單元正方形都用有限集合
,它們是一對相鄰的單元正方形,每個單元正方形都用有限集合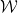 中的一個元素點來點綴,是否可以在標準格密舖
中的一個元素點來點綴,是否可以在標準格密舖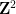 #中為每個單元正方形分配一個點,使得這個密舖中的每一對水平(或垂直)的方格都能用到來自
#中為每個單元正方形分配一個點,使得這個密舖中的每一對水平(或垂直)的方格都能用到來自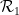 或
或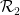 的骨牌?
的骨牌?

事實上,我們只需要將每個王氏密舖作為一個單獨的「點」插入,並定義骨牌集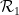 ,
,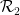 為水平或垂直相鄰、邊緣具有相同顏色的王氏密鋪對。
為水平或垂直相鄰、邊緣具有相同顏色的王氏密鋪對。
在接下來的步驟中,我們將把骨牌問題與數獨問題結合:#

問題4(數獨問題)
給定列寬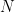 #、數字集
#、數字集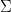 、函數
、函數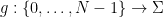 的集合
的集合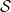 #與「初始條件」
#與「初始條件」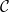 #(這裡就不詳細介紹了),是否可以為「數獨棋盤」
#(這裡就不詳細介紹了),是否可以為「數獨棋盤」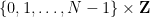 中的每個單元格
中的每個單元格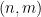 分配一個數字
分配一個數字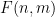 ,以便對於任何斜率
,以便對於任何斜率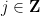 和截距
和截距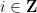 ,沿著
,沿著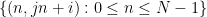 線的數字
線的數字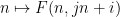 位於
位於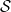 #中(並且
#中(並且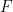 服從初始條件
服從初始條件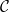 )?
)?
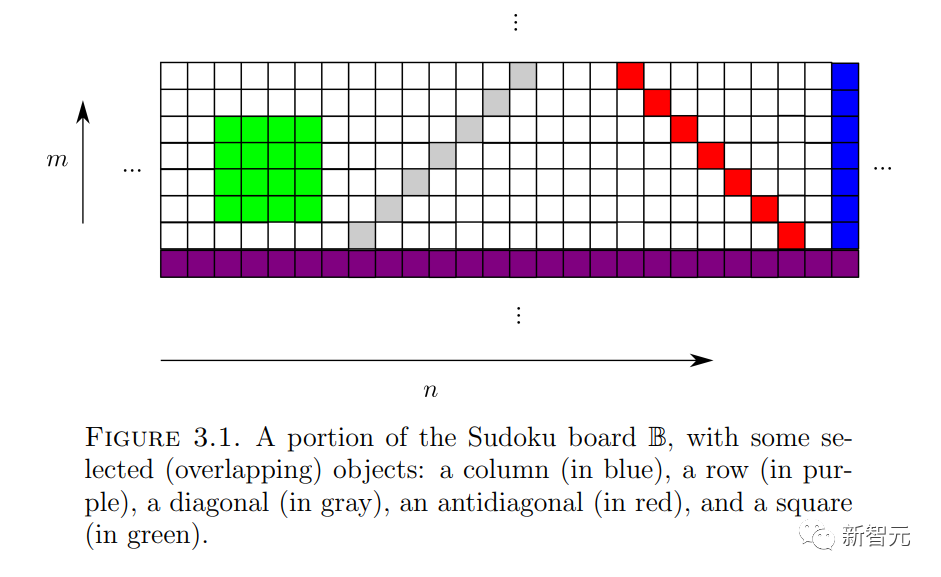
這篇論文最新穎的部分是證明了骨牌問題確實可以嵌入到數獨問題中。
將數獨問題嵌入到單密鋪問題中,是基於先前論文中提出的修改方法
這些論文也提出了數獨問題的不同版本,並創造了一種名為「密舖語言」的方法,可以將各種問題(包括數獨問題)轉化為單一的密舖問題
要將骨牌問題編碼為數獨問題,我們需要取得一個多米諾函數
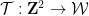 #(遵守與某些骨牌集
#(遵守與某些骨牌集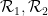
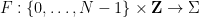
這種做法並不是很顯而易見,但是在Emmanuel Jeandel的幫助下,陶哲軒和Rachel Greenfeld改編了Aanderaa和Lewis的一些想法,某些層次結構被用來將一個問題編碼另一個問題。
在這裡,我們解釋分層結構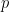 (由於骨牌問題的二維性,需要使用兩個不同的質數)。
(由於骨牌問題的二維性,需要使用兩個不同的質數)。
然後,透過公式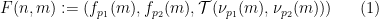 用
用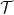 #建構數獨函數
#建構數獨函數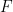 ,它將體現某種嵌入。
,它將體現某種嵌入。
其中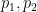 是兩個不同的大質數(例如,可以取
是兩個不同的大質數(例如,可以取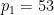 ,
,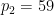 #),
#),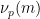 表示
表示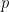 除以
除以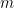 #的次數,並且
#的次數,並且
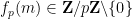 是
是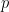 的
的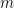
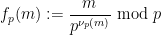
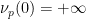
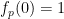
,且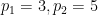 )。
)。
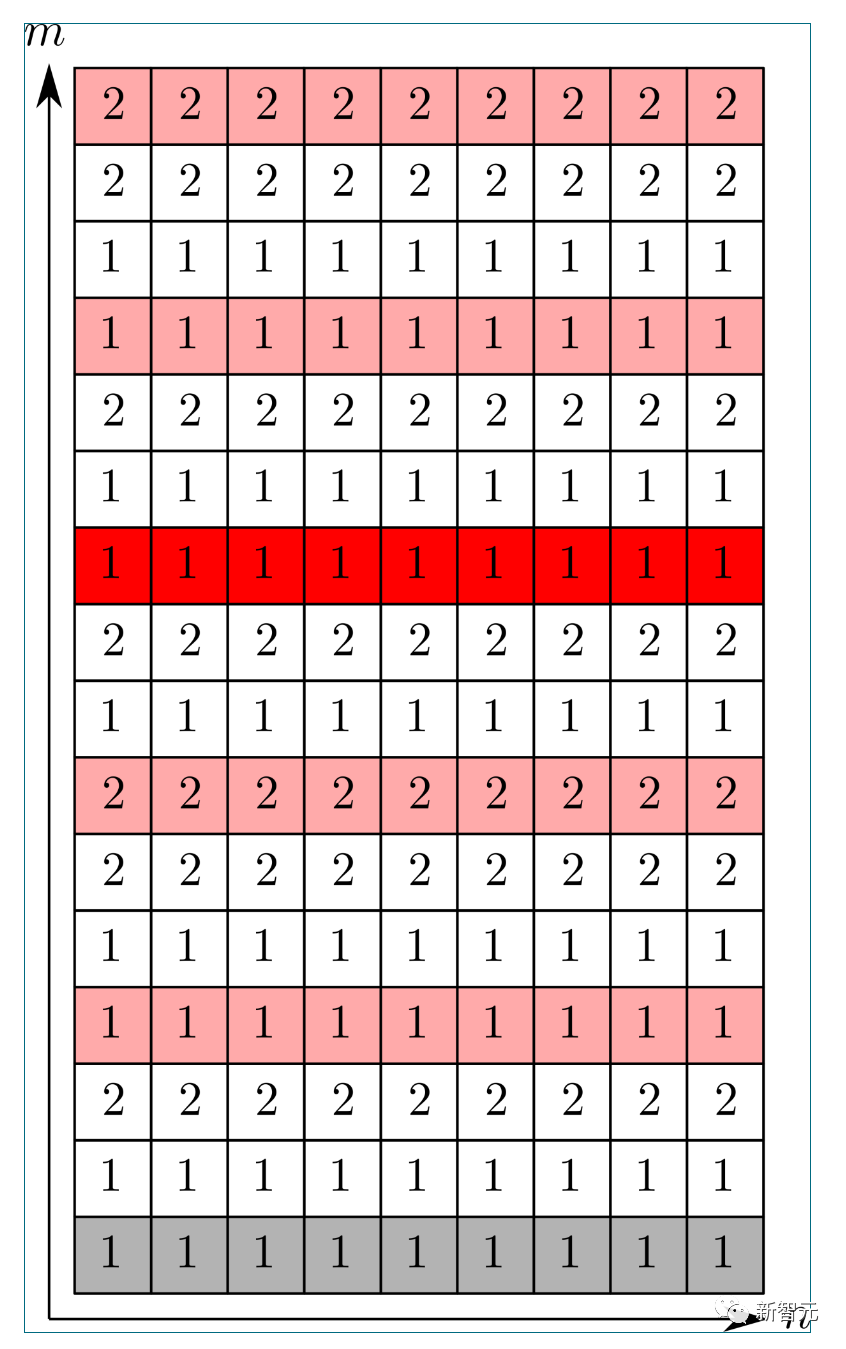
的情況下,(1) 的第一個分量如下所示: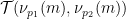
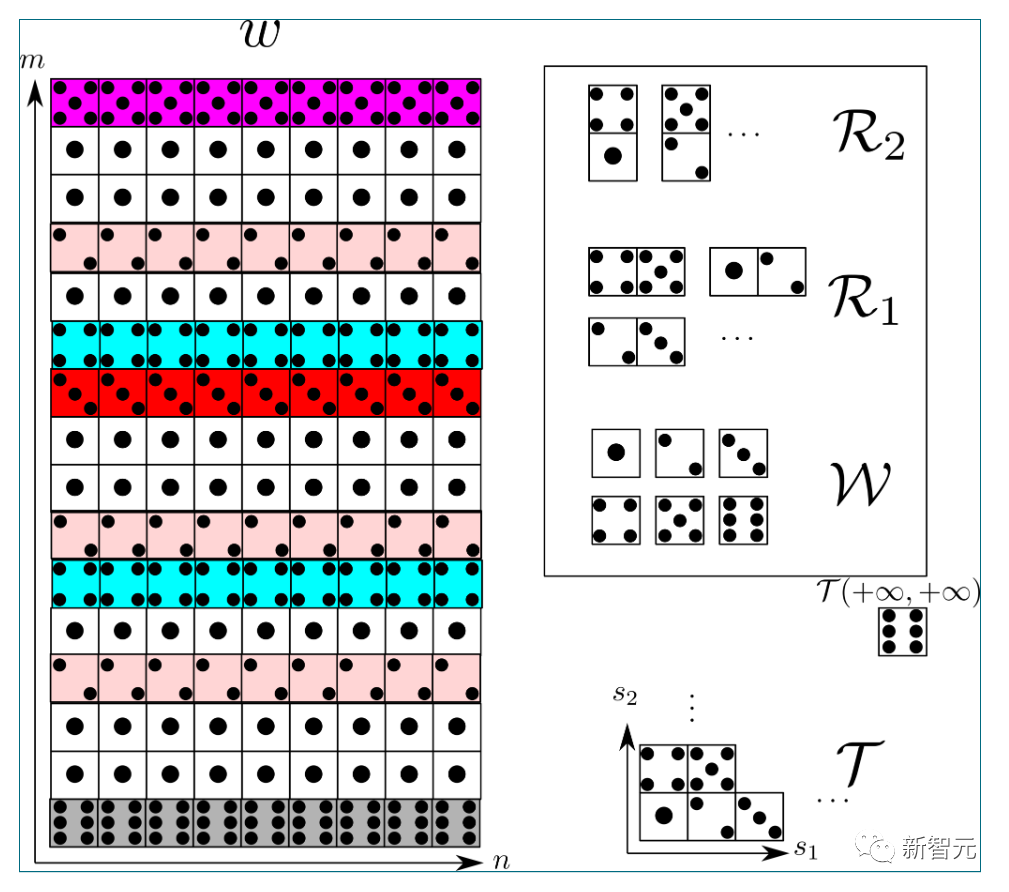
的典型實例如下所示:
##################有趣的是,不知道為什麼,這裡的裝飾基本上遵循了兒童遊戲“Fizz buzz”的規則######以上是陶哲軒再逼近60年幾何學難題!週期性密鋪問題又獲新突破的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 AI顛覆數學研究!菲爾茲獎得主、華裔數學家領銜11篇頂刊論文|陶哲軒轉贊
Apr 09, 2024 am 11:52 AM
AI顛覆數學研究!菲爾茲獎得主、華裔數學家領銜11篇頂刊論文|陶哲軒轉贊
Apr 09, 2024 am 11:52 AM
AI,的確正在改變數學。最近,一直十分關注這個議題的陶哲軒,轉發了最近一期的《美國數學學會通報》(BulletinoftheAmericanMathematicalSociety)。圍繞著「機器會改變數學嗎?」這個話題,許多數學家發表了自己的觀點,全程火花四射,內容硬核,精彩紛呈。作者陣容強大,包括菲爾茲獎得主AkshayVenkatesh、華裔數學家鄭樂雋、紐大電腦科學家ErnestDavis等多位業界知名學者。 AI的世界已經發生了天翻地覆的變化,要知道,其中許多文章是在一年前提交的,而在這一
 七邊形數
Sep 24, 2023 am 10:33 AM
七邊形數
Sep 24, 2023 am 10:33 AM
Aheptagonalnumberisanumberwhichcanberepresentedasaheptagon.Aheptagonisapolygonwith7sides.Aheptagonalnumbercanberepresentedasacombinationofsuccessivelayersofheptagon(7-sidedpolygon).Heptagonalnumbercanbebetterexpexpmedwiththebelowgures.第一個七邊形數是第一個七邊形數。因此,
 MLP一夜被幹掉! MIT加州理工等革命性KAN破紀錄,發現數學定理碾壓DeepMind
May 06, 2024 pm 03:10 PM
MLP一夜被幹掉! MIT加州理工等革命性KAN破紀錄,發現數學定理碾壓DeepMind
May 06, 2024 pm 03:10 PM
一夕之間,機器學習範式要變天了!現今,統治深度學習領域的基礎架構是,多層感知器(MLP)-將活化函數放置在神經元上。那麼,除此之外,我們是否還有新的路線可走?就在今天,來自MIT、加州理工、東北大學等機構的團隊重磅發布了,全新的神經網路結構-Kolmogorov–ArnoldNetworks(KAN)。研究人員對MLP做了一個簡單的改變,即將可學習的活化函數從節點(神經元)移到邊(權重)上!論文地址:https://arxiv.org/pdf/2404.19756這個改變乍聽之下似乎毫無根據
 開創性CVM演算法破解40多年計數難題!電腦科學家擲硬幣算出「哈姆雷特」獨特單字
Jun 07, 2024 pm 03:44 PM
開創性CVM演算法破解40多年計數難題!電腦科學家擲硬幣算出「哈姆雷特」獨特單字
Jun 07, 2024 pm 03:44 PM
計數,聽起來簡單,卻在實際執行上很困難。想像一下,你被送到一片原始熱帶雨林,進行野生動物普查。每當看到一隻動物,就拍一張照片。數位相機只是記錄追蹤動物總數,但你對獨特動物的數量感興趣,卻沒有統計。那麼,若想獲取這獨特動物數量,最好的方法是什麼?這時,你一定會說,從現在開始計數,最後再從照片中將每一種新物種與名單進行比較。然而,這種常見的計數方法,有時並不適用於高達數十億條目的資訊量。來自印度統計研究所、UNL、新加坡國立大學的電腦科學家提出了一種新演算法——CVM。它可以近似計算長列表中,不同條
 AI繪畫,還需要懂數學?
Jun 12, 2023 pm 02:05 PM
AI繪畫,還需要懂數學?
Jun 12, 2023 pm 02:05 PM
視覺隨著人工智慧技術的發展,AI繪畫成為當下的熱門話題。透過使用深度學習演算法,人工智慧可以產生逼真的圖像,從而創造出驚人的藝術品。而這些驚人的作品背後,離不開數學知識的支持。數學模型在AI繪畫中扮演著至關重要的角色。一方面,數學模型被用來描述和表示圖像訊息,從而讓電腦能夠理解和處理圖像。另一方面,數學模型也被用來訓練深度學習模型,從而實現影像的自動生成。深度學習模型帶來高品質的圖像生成深度學習模型是AI繪畫中最核心的部分。它透過學習大量的影像資料來識別和模擬影像的特徵,透過多層次的資料處理
 「數學菜雞」ChatGPT很懂人類喜好!在線生成隨機數,竟是宇宙終極答案
Apr 01, 2023 am 11:48 AM
「數學菜雞」ChatGPT很懂人類喜好!在線生成隨機數,竟是宇宙終極答案
Apr 01, 2023 am 11:48 AM
ChatGPT在產生隨機數字方面,也是玩明白了人類的套路。 ChatGPT可能是一位廢話藝術家、錯誤訊息的傳播者,但它不是「數學家」!近日,一位Meta的資料科學家Colin Fraser發現,ChatGPT並不能產生真正的隨機數,而更像是「人類的隨機數」。透過實驗,Fraser得出的結論是:「ChatGPT非常喜歡數字42和7。」網友表示,意味著人類非常喜歡這些數字。 ChatGPT也愛「宇宙終極答案」在他的測驗中,Fraser輸入的prompt如下:「Pick a random number
 擴散模型背後數學太難了,啃不動?谷歌用統一視角講明白了
Apr 11, 2023 pm 07:46 PM
擴散模型背後數學太難了,啃不動?谷歌用統一視角講明白了
Apr 11, 2023 pm 07:46 PM
最近一段時間,AI 作畫可謂是火的一塌糊塗。在你驚嘆 AI 繪畫能力的同時,可能還不知道的是,擴散模型在其中扮演了重大角色。就拿熱門模型 OpenAI 的 DALL·E 2 來說,只要輸入簡單的文字(prompt),它就可以產生多張 1024*1024 的高清影像。在 DALL·E 2 公佈沒多久,谷歌隨後發布了 Imagen,這是一個文本到圖像的 AI 模型,它能夠通過給定的文本描述生成該場景下逼真的圖像。就在前幾天,Stability.Ai 公開發布文字生成圖像模型 Stable Diffusi
 白天打工,晚上科研,Google大腦研究科學家解決了困擾數學界幾十年的猜想
Apr 12, 2023 am 09:49 AM
白天打工,晚上科研,Google大腦研究科學家解決了困擾數學界幾十年的猜想
Apr 12, 2023 am 09:49 AM
2022 年 10 月中旬,Justin Gilmer 從加州飛往紐約,在東海岸拜訪了他以前的導師 Michael Saks,一位羅格斯大學的數學家。敘舊期間,他們並未談到數學。事實上,自從 2015 年在羅格斯大學獲得博士學位後,Gilmer 就再也沒認真思考過數學問題。那時候他決定不在學術界發展,同時開始自學程式設計。當他和 Saks 共同用餐時,Gilmer 向導師講述了他在谷歌的工作:機器學習和人工智慧。在校園的小路上,Gilmer 邊走邊回憶,2013 年,他花了一年多的時間走在這條






