參數少近一半，效能逼近谷歌Minerva，又一個數學大模型開源了-人工智慧-PHP中文網

如今，在各種文字混合資料上訓練出來的語言模型會顯示出非常通用的語言理解和生成能力，可以作為基礎模型適應各種應用。開放式對話或指令追蹤等應用要求在整個自然文本分佈中實現均衡的效能，因此更傾向於通用模型。

不過如果想要在某一領域（如醫學、金融或科學）內最大限度地提高效能，那麼特定領域的語言模型可能會以給定的計算成本提供更優越的能力，或以更低的計算成本提供給定的能力水準。

普林斯頓大學、 EleutherAI 等的研究者為解決數學問題訓練了一個特定領域的語言模型。他們認為：首先，解決數學問題需要與大量的專業先驗知識進行模式匹配，因此是進行領域適應性訓練的理想環境；其次，數學推理本身就是AI 的核心任務；最後，能夠進行強數學推理的語言模型是許多研究主題的上游，如獎勵建模、推理強化學習和演算法推理。

因此，他們提出一種方法，透過對 Proof-Pile-2 進行持續的預訓練，使語言模型適應數學。 Proof-Pile-2 是數學相關文字和程式碼的混合資料。將此方法應用於 Code Llama，可以得到 LLEMMA：7B 和 34B 的基礎語言模型，其數學能力得到了大幅提升。

參數少近一半，效能逼近谷歌Minerva，又一個數學大模型開源了

論文網址：https://arxiv.org/pdf/2310.10631.pdf

#專案地址：https://github.com/EleutherAI/math-lm

LLEMMA 7B 的4-shot Math 效能遠超GoogleMinerva 8B，LLEMMA 34B 在參數少近一半的情況下效能逼近Minerva 62B。

參數少近一半，效能逼近谷歌Minerva，又一個數學大模型開源了

具體來說，本文貢獻如下：

##1. 訓練並發布了LLEMMA 模型：專門用於數學的7B 和34B 語言模型。 LLEMMA 模型是在 MATH 上公開發布的基礎模型的最新水平。
2. 發布了代數堆疊（AlgebraicStack），這是一個包含 11B 專門與數學相關的程式碼 token 的資料集。
3. 證明了 LLEMMA 能夠使用計算工具來解決數學問題，即 Python 解釋器和形式定理證明器。
4. 與先前的數學語言模型（如 Minerva）不同，LLEMMA 模型是開放式的。研究者開放了訓練資料和程式碼。這使得 LLEMMA 成為未來數學推理研究的一個平台。

方法概覽

LLEMMA 是專門用於數學的 70B 和 34B 語言模型。它由 Proof-Pile-2 上繼續對代碼 Llama 進行預訓練得到的。

#DATA: Proof-Pile-2

研究者創建了Proof-Pile-2，這是一個55B token 的科學論文、包含數學的網路資料和數學程式碼的混合。除了 Lean proofsteps 子集之外，Proof-Pile-2 的知識截止日期為 2023 年 4 月。

參數少近一半，效能逼近谷歌Minerva，又一個數學大模型開源了

數值模擬、電腦代數系統和形式定理證明器等計算工具對數學家的重要性與日俱增。因此，研究者創建了代數堆疊（AlgebraicStack），這是一個包含 17 種語言原始碼的 11B token 資料集，涵蓋數值數學、符號數學和形式數學。此資料集由來自 Stack、GitHub 公共資源庫和形式證明步驟資料的過濾程式碼組成。表9顯示了AlgebraicStack 中各語言的 token 數量。

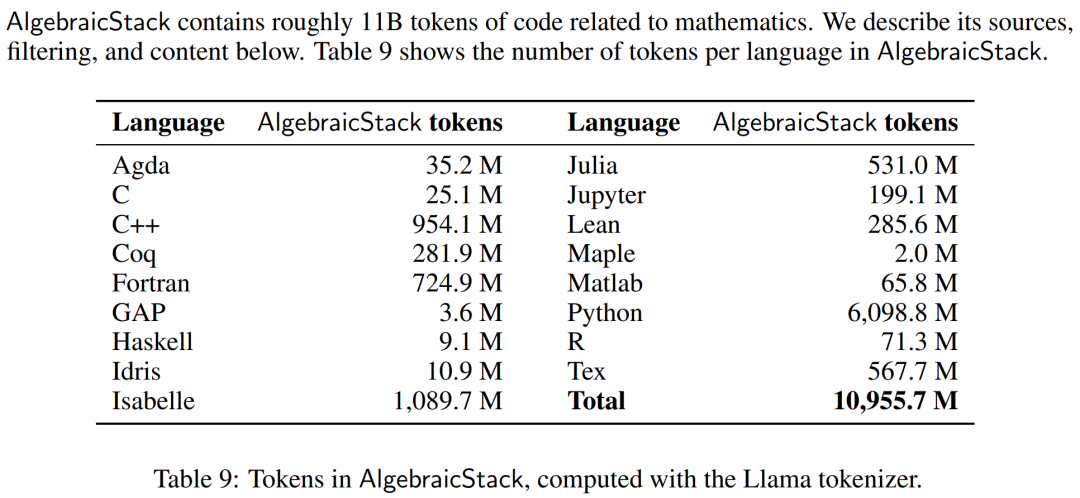
參數少近一半，效能逼近谷歌Minerva，又一個數學大模型開源了

AlgebraicStack 中各語言的 token 數。

研究者了使用 OpenWebMath，這是一個由高品質網頁組成的 15B token 資料集，其中過濾了數學內容。 OpenWebMath 根據數學相關關鍵字和基於分類器的數學評分過濾 CommonCrawl 網頁，保留數學格式（如 LATEX、AsciiMath），並包含額外的質量過濾器（如 plexity、domain、length）和近似重複。

除此之外，研究者也使用了 RedPajama 的 ArXiv 子集，它是 LLaMA 訓練資料集的開放再現。 ArXiv 子集包含 29B 個字塊。訓練混合資料由少量一般領域資料組成，起到了正規化的作用。由於 LLaMA 2 的預訓練資料集尚未公開，研究者使用 Pile 作為替代訓練資料集。

模型與訓練

每個模型都是從Code Llama 初始化而來，該模型又初始化自Llama 2，使用僅解碼器（deconder only）的transformer 結構，在500B 的程式碼token 上訓練而成。研究者使用標準自回歸語言建模目標，在 Proof-Pile-2 上繼續訓練 Code Llama 模型。這裡，LLEMMA 7B 模型有 200B token，LLEMMA 34B 模型有 50B token。

研究者使用 GPT-NeoX 函式庫在 256 個 A100 40GB GPU 上，以 bfloat16 混合精度來訓練以上兩個模型。他們為 LLEMMA-7B 使用了世界大小為 2 的張量並行，為 34B 使用了世界大小為 8 的張量並行，以及跨資料並行副本的 ZeRO Stage 1 分片優化器狀態。此外還使用 Flash Attention 2 來提高吞吐量並進一步降低記憶體需求。

LLEMMA 7B 經過了 42000 步驟的訓練，全域 batch 大小為 400 萬個 token，上下文長度為 4096 個 token。這相當於 23000 個 A100 時。學習率在 500 步後預熱到了 1・10^−4，然後在 48000 步後將餘弦衰減到最大學習率的 1/30。

LLEMMA 34B 經過了 12000 步的訓練，全域 batch 大小同樣為 400 萬個 token，上下文長度為 4096。這相當於 47000 個 A100 時。學習率在 500 步後預熱到了 5・10^−5，然後衰減到峰值學習率的 1/30。

評估結果

在實驗部分，研究者旨在評估 LLEMMA 是否可以作為數學文本的基礎模型。他們利用少樣本評估來比較 LLEMMA 模型，並主要關注沒有在數學任務監督樣本上進行微調的 SOTA 模型。

研究者首先使用思維鏈推理和多數投票（majority voting）方法來評估 LLEMMA 求解數學題的能力，評估基準包括了 MATH 和 GSM8k。然後探索使用少樣本工具和定理證明。最後研究了記憶體和資料混合的影響。

使用思維鏈（CoT）來解數學題

這些任務包含LATEX 或自然語言表示的問題產生獨立的文字答案，而無需使用外部工具。研究者使用到的評估基準有 MATH、GSM8k、 OCWCourses、SAT 和 MMLU-STEM。

結果如下表1 所示，LLEMMA 在Proof-Pile-2 語料庫上的持續預訓練在5 個數學基准上均提升了少樣本性能，其中LLEMMA 34B 在GSM8k上比Code Llama 提高了20 個百分點，在MATH 上比Code Llama 提高了13 個百分點。同時 LLEMMA 7B 優於專有的 Minerva 模型。

因此，研究者得到結論，在 Proof-Pile-2 上進行持續預訓練有助於提升預訓練模型求解數學題的能力。

參數少近一半，效能逼近谷歌Minerva，又一個數學大模型開源了