陶哲軒瘋狂安麗Copilot:它幫我完成了一頁紙證明,甚至能猜出我後面的過程
繼給GPT-4「代言」之後,Copilot也被陶哲軒瘋狂安麗。
他直言,在程式設計時,Copilot能直接預測他下一步要做什麼。
有了Copilot之後,研究做起來也更方便了,陶哲軒也用它輔助自己完成了最新的研究成果。

陶哲軒說,這次的論文中,有關這部分的內容其實只有一頁。
但具體完成這一頁紙的證明,他足足寫了200多行程式碼,用的還是新學的程式語言Lean4。

而在陶哲軒公開程式碼的GitHub頁面上顯示,Copilot將寫程式碼的速度提升了一半以上。
陶哲軒介紹,之所以選擇Lean4是看中了它的“重寫策略”,也就是對一長段表達式進行針對性的局部替換。
舉個例子,假如定義了一個複雜的函數f(x),當我們想要輸入f(114514)的表達式時,直接用程式碼把x「重寫」成114514就可以了。
陶哲軒說,這個特性比起需要重複輸入公式的LaTeX簡直不要太方便。
那麼陶哲軒這次的「一頁紙證明」又為我們帶來了什麼新成果呢?
一頁紙證明新不等式
這篇論文談論了有關麥克勞林不等式的問題。
麥克勞林不等式是數學中一個經典的不等式,它基於「非負實數的算數平均值大於等於幾何平均值」這一定律導出,可以表述為:
設y1…yn為非負實數,對k=1…n,定義平均值Sk為(分母為分子的項數):
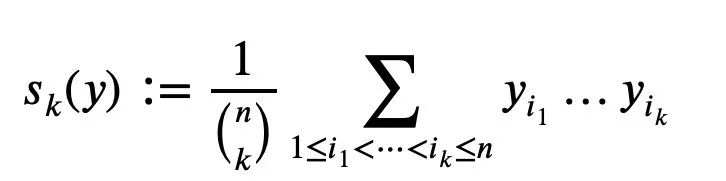
它是作為具有根的n 次多項式的歸一化係數而出現。
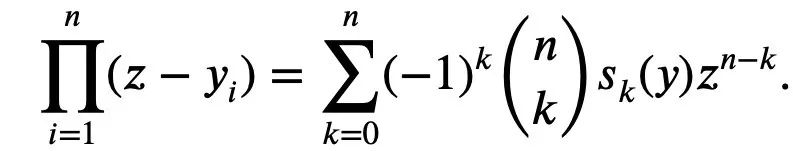
(記得這個式子,我們稱它為式1)
則麥克勞林不等式可以表示為:
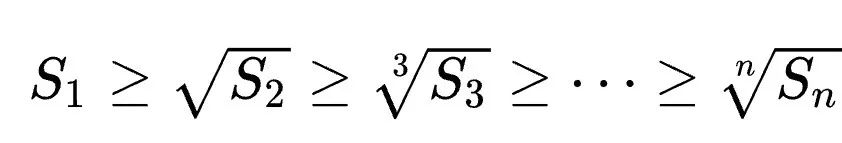
#其中,當且僅當所有yi相等時等號成立。
在微積分中,還有一個經典的牛頓不等式:
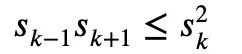
對任意1≤k
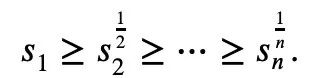
#但如果不加上這個限制條件,即允許負數項的存在,用牛頓不等式就無法表示麥克勞林不等式了。
於是針對牛頓不等式中可能存在負數項的情況,陶哲軒提出了一組新的不等式變體:
對任意r>0且1≤ℓ≤n,必有式2或式3成立。
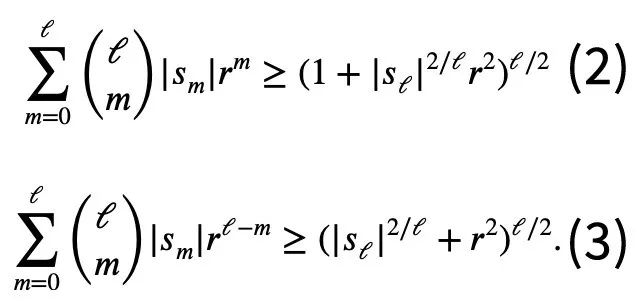
這便是陶哲軒這一頁紙所要證明的內容,具體證明過程是這樣的:
不妨建構一個關於複雜變數z的多項式P(z):
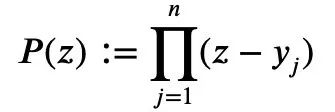
由前面的式1和三角不等式可得:
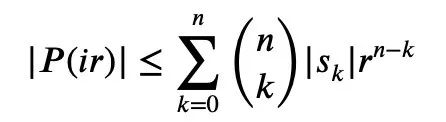
所以只需要建立下界:
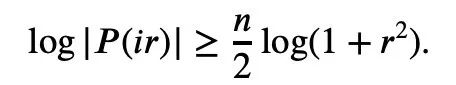
對P(z)取絕對值再取對數可得:
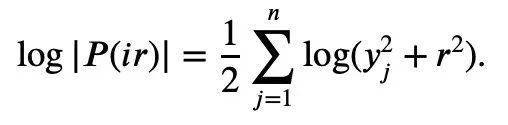
由於對任意實數t,t ↦ log(et a)呈凸性且a>0,可以得到不等式:
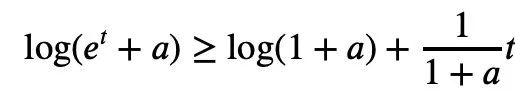
當a=r2,t=2log yj時,可以得到:
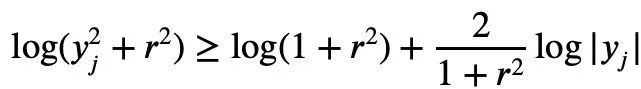
以上就是陶哲軒給出的證明過程,但是,當歸一化的|Sn|=1時,下式成立:
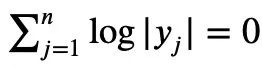
下一步:建立細化版本
除了這次提到的“一頁紙證明”,陶哲軒的這篇論文中還提出了另一項新的定理,即對任意1 ≤ k ≤ ℓ≤ n.:
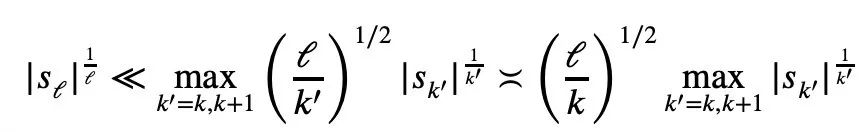
在部落格文章中,陶哲軒透露,他的下一步計畫就是提出這一不等式的細化版本。
陶哲軒說,證明的過程「就像練習一樣」會很簡單,用微積分就能搞定。
不過,他也提到會有一個小困難,因為這部分論證過程使用到了漸進符號。

新的結論具體怎樣,讓我們拭目以待。
One More Thing
陶哲軒可謂是AI工具的忠實粉絲,Copilot、GPT-4,還有一些其他輔助工具都受到他的推薦。
這次,他也對大模型的發展提出了新的期待,希望有一天模型可以直接產生不等式變體。

論文網址:https://arxiv.org/abs/2310.05328
#以上是陶哲軒瘋狂安麗Copilot:它幫我完成了一頁紙證明,甚至能猜出我後面的過程的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 數字貨幣app是啥軟件?全球數字貨幣十大app盤點
Apr 30, 2025 pm 07:06 PM
數字貨幣app是啥軟件?全球數字貨幣十大app盤點
Apr 30, 2025 pm 07:06 PM
隨著數字貨幣的普及和發展,越來越多的人開始關注和使用數字貨幣app。這些應用程序為用戶提供了便捷的管理和交易數字資產的方式。那麼,數字貨幣app到底是什麼軟件呢?讓我們深入了解,並盤點全球十大數字貨幣app。
 量化交易所排行榜2025 數字貨幣量化交易APP前十名推薦
Apr 30, 2025 pm 07:24 PM
量化交易所排行榜2025 數字貨幣量化交易APP前十名推薦
Apr 30, 2025 pm 07:24 PM
交易所內置量化工具包括:1. Binance(幣安):提供Binance Futures量化模塊,低手續費,支持AI輔助交易。 2. OKX(歐易):支持多賬戶管理和智能訂單路由,提供機構級風控。獨立量化策略平台有:3. 3Commas:拖拽式策略生成器,適用於多平台對沖套利。 4. Quadency:專業級算法策略庫,支持自定義風險閾值。 5. Pionex:內置16 預設策略,低交易手續費。垂直領域工具包括:6. Cryptohopper:雲端量化平台,支持150 技術指標。 7. Bitsgap:
 數字貨幣app是正規的嗎?全球正規合法虛擬幣交易app前十
Apr 30, 2025 pm 07:09 PM
數字貨幣app是正規的嗎?全球正規合法虛擬幣交易app前十
Apr 30, 2025 pm 07:09 PM
推薦的加密貨幣交易平台包括:1. Binance:全球最大交易量,支持1400 幣種,FCA、MAS認證。 2. OKX:技術實力強,支持400 幣種,香港證監會批准。 3. Coinbase:美國最大合規平台,適合新手,SEC和FinCEN監管。 4. Kraken:歐洲老牌,ISO 27001認證,持美國MSB及英國FCA牌照。 5. Gate.io:幣種最全(800 ),低交易費,獲多國牌照。 6. Huobi Global:老牌平台,提供多種服務,持日本FSA及香港TCSP牌照。 7. KuCoin
 數字貨幣app有前途嗎 蘋果手機數字貨幣交易平台app下載TOP10
Apr 30, 2025 pm 07:00 PM
數字貨幣app有前途嗎 蘋果手機數字貨幣交易平台app下載TOP10
Apr 30, 2025 pm 07:00 PM
數字貨幣App的前景廣闊,具體體現在:1. 技術創新驅動功能升級,通過DeFi與NFT融合及AI與大數據應用提升用戶體驗;2. 監管合規化趨勢,全球框架完善及AML、KYC要求趨嚴;3. 功能多元化與服務拓展,整合借貸、理財等服務並優化用戶體驗;4. 用戶基數與全球化擴張,預計2025年用戶規模突破10億。
 香港數字貨幣交易所app如何下載 十大數字貨幣交易所APP盤點
Apr 30, 2025 pm 07:12 PM
香港數字貨幣交易所app如何下載 十大數字貨幣交易所APP盤點
Apr 30, 2025 pm 07:12 PM
下載香港數字貨幣交易所APP的方法包括:1. 選擇合規平台,如OSL、HashKey或Binance HK等;2. 通過官方渠道下載,iOS用戶在App Store下載,Android用戶通過Google Play或官網下載;3. 註冊並驗證身份,使用香港手機號或郵箱,上傳身份和地址證明;4. 設置安全措施,啟用雙重身份驗證並定期檢查賬戶活動。
 幣安廣場怎麼樣可靠嗎
May 07, 2025 pm 07:18 PM
幣安廣場怎麼樣可靠嗎
May 07, 2025 pm 07:18 PM
幣安廣場(Binance Square)是幣安交易所提供的一個社交媒體平台,旨在為用戶提供一個交流和分享加密貨幣相關信息的空間。本文將詳細探討幣安廣場的功能、可靠性以及用戶體驗,幫助你更好地了解這個平台。
 歐意OKX6.118.0版本最新下載教程
May 07, 2025 pm 06:51 PM
歐意OKX6.118.0版本最新下載教程
May 07, 2025 pm 06:51 PM
歐意OKX6.118.0版本最新下載教程:1、點擊文章中快捷鏈接;2、點擊下載即可(如果是網頁用戶請先進行信息註冊)。最新安卓版本v6.118.0優化了部分功能和體驗,讓交易更容易。立即更新App,感受更加極致的交易體驗。
 2025幣安在線網頁地址
May 07, 2025 pm 06:54 PM
2025幣安在線網頁地址
May 07, 2025 pm 06:54 PM
幣安(Binance)作為全球領先的加密貨幣交易所,始終致力於為用戶提供安全、便捷的交易體驗。隨著時間的推移,幣安不斷優化其平台功能和用戶界面,以滿足用戶不斷變化的需求。 2025年,幣安推出了新的登錄入口,旨在進一步提升用戶體驗。






