在機器學習領域中,相關模型可能會在訓練過程中變得過度擬合和欠擬合。為了防止這種情況的發生,我們在機器學習中使用正規化操作來適當地讓模型擬合在我們的測試集上。一般來說,正規化操作透過降低過度擬合和欠擬合的可能性來幫助大家獲得最佳模型。
在本文中,我們將了解什麼是正規化,正規化的類型。此外,我們將討論偏差、變異數、欠擬合和過度擬合等相關概念。
我們不再是廢話,直接開始吧!
Bias與Variance是用來描述我們學習到的模型與真實模型之間差距的兩個面向
需要被改寫的是:二者的定義如下:
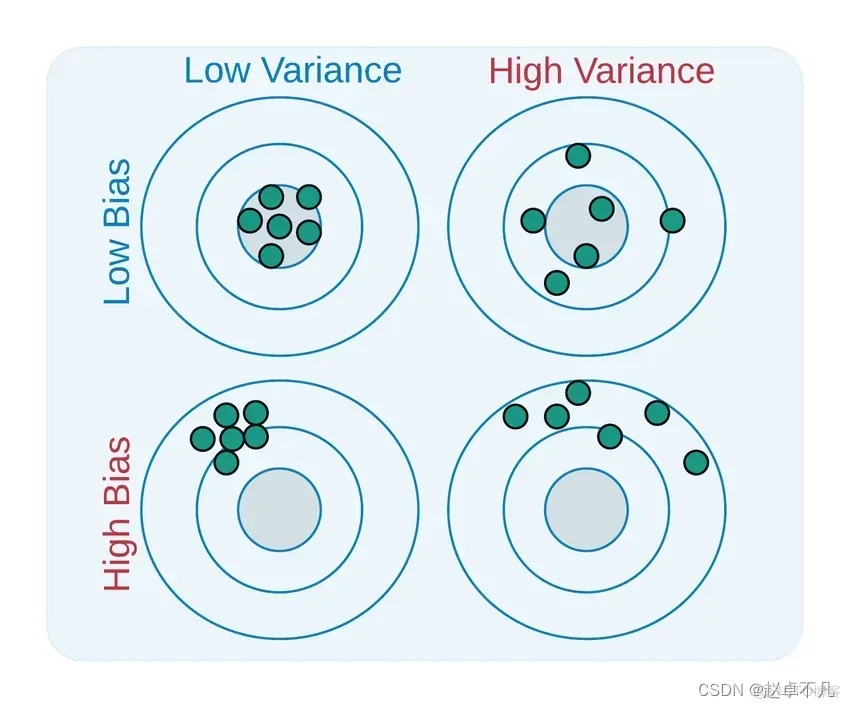
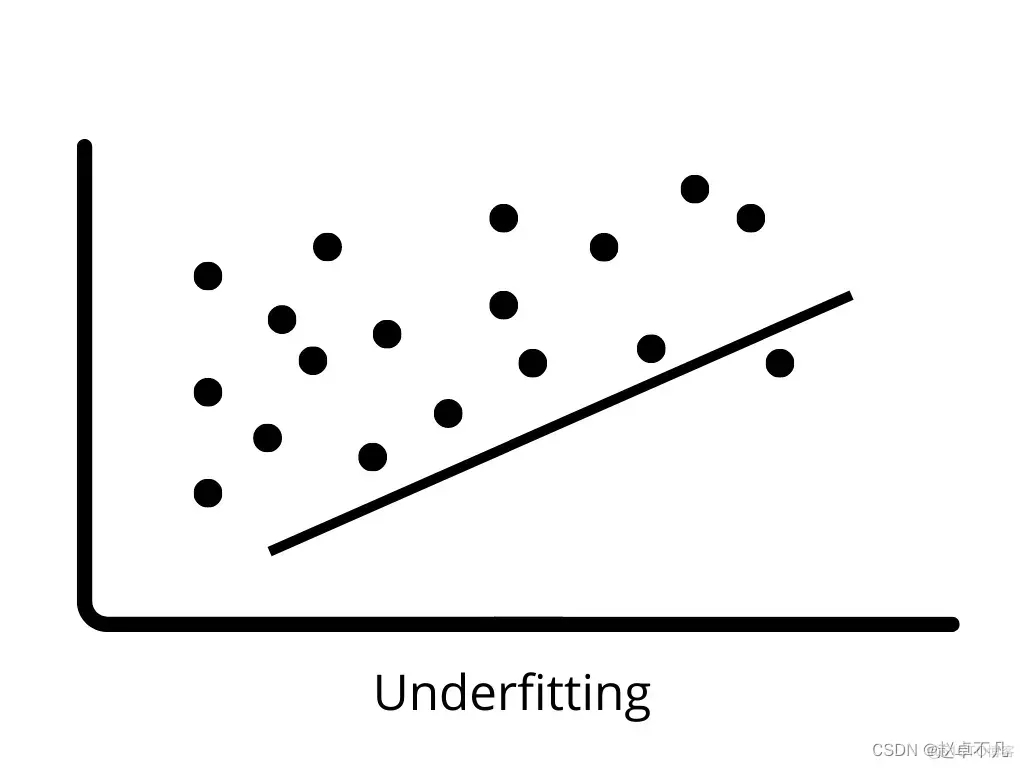
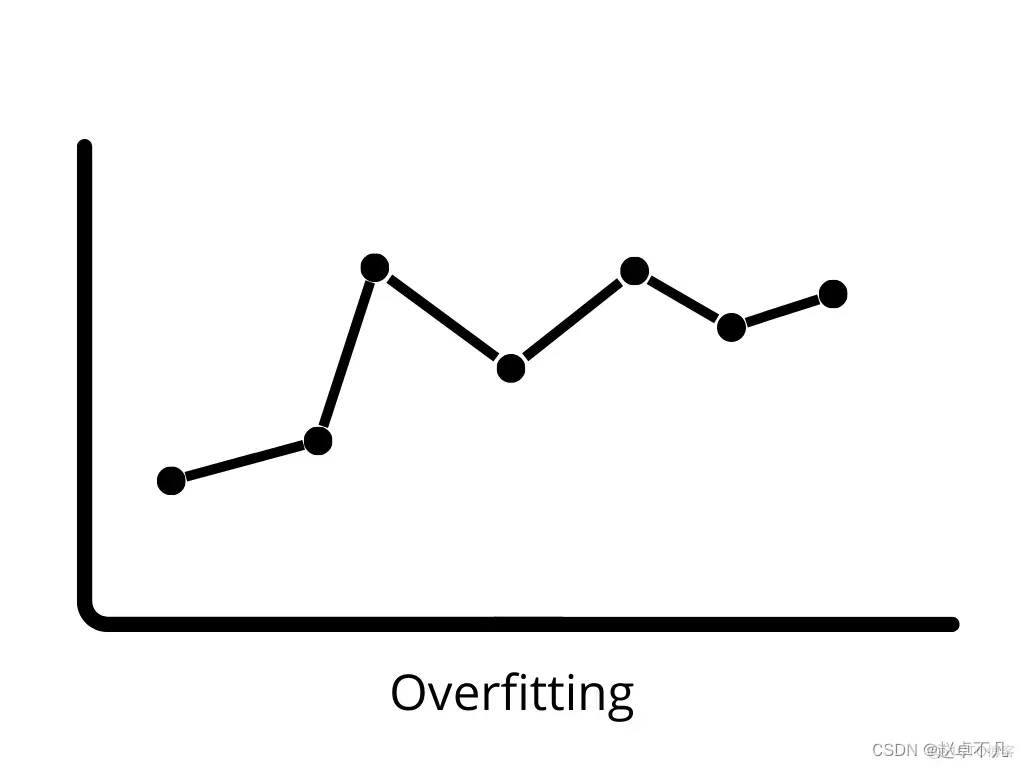
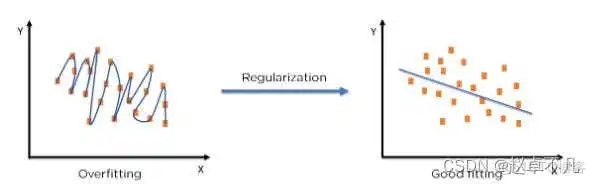
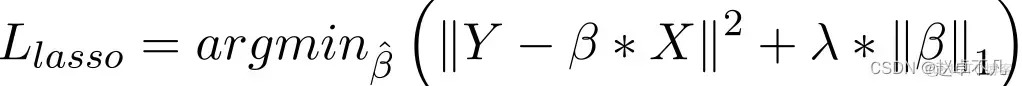 #透過使用正則化技術,我們可以讓機器學習模型更加準確地擬合到特定的測試集上,從而有效降低測試集中的誤差
#透過使用正則化技術,我們可以讓機器學習模型更加準確地擬合到特定的測試集上,從而有效降低測試集中的誤差
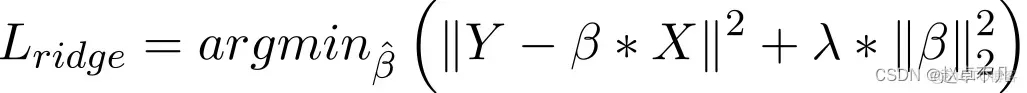 在Lasso迴歸模型中,以類似於嶺迴歸的方式透過增加迴歸係數的絕對值這一懲罰項來實現。此外,L1正則化在提高線性迴歸模型的精確度方面有著良好的表現。同時,由於L1正則化對所有參數的懲罰力度都一樣,可以讓一部分權重變為零,因此產生稀疏模型,能夠去除某些特徵(權重為0則等效於去除)。
在Lasso迴歸模型中,以類似於嶺迴歸的方式透過增加迴歸係數的絕對值這一懲罰項來實現。此外,L1正則化在提高線性迴歸模型的精確度方面有著良好的表現。同時,由於L1正則化對所有參數的懲罰力度都一樣,可以讓一部分權重變為零,因此產生稀疏模型,能夠去除某些特徵(權重為0則等效於去除)。
一般而言,當資料表現出多重共線性(自變數高度相關)時,它被認為是一種採用的方法。儘管多重共線性中的最小平方法估計值 (OLS) 是無偏的,但它們的巨大變異會導致觀測值與實際值相差很大。 L2透過在一定程度上降低了迴歸估計值的誤差。它通常使用收縮參數來解決多重共線性問題。 L2正則化減少了權重的固定比例,使權重平滑。
經過上述分析,對本文中相關正規化的知識進行總結如下:
L1正則化可以產生稀疏權值矩陣,即產生一個稀疏模型,可以用於特徵選擇;
L2正則化可以防止模型過擬合,在在某種程度上,L1也可以防止過度擬合,提升模型的泛化能力;
L1(拉格朗日)正則假設參數的先驗分佈是Laplace分佈,可以保證模型的稀疏性,也就是某些參數等於0;
L2(嶺迴歸)的假設是參數的先驗分佈是高斯分佈,這可以確保模型的穩定性,即參數的值不會過大或過小
在實際應用中,如果特徵是高維度稀疏的,就應該使用L1正則化;如果特徵是低維密集的,就應該使用L2正則化
以上是什麼是機器學習中的正規化?的詳細內容。更多資訊請關注PHP中文網其他相關文章!




