繼上次盤點《資料科學家95%的時間都在使用的11個基本圖表》之後，今天將為大家帶來資料科學家95%的時間都在使用的11個基本分佈。掌握這些分佈，有助於我們更深入地理解數據的本質，並在數據分析和決策過程中做出更準確的推論和預測。
1. 常態分佈
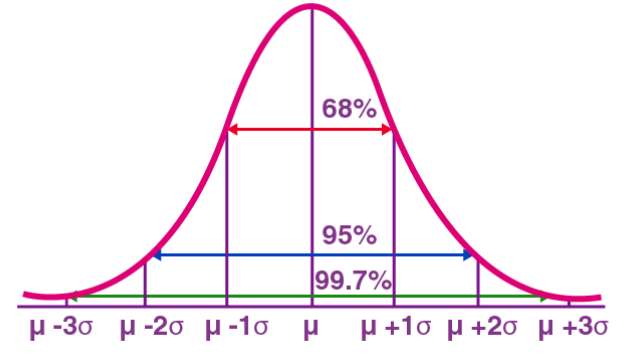
常態分佈（Normal Distribution），也稱為高斯分佈（Gaussian Distribution），是一種連續型機率分佈。它具有一個對稱的鐘形曲線，以平均值（μ）為中心，標準差（σ）為寬度。常態分佈在統計學、機率論、工程學等多個領域具有重要的應用價值。
常態分佈的機率密度函數可以表示為：
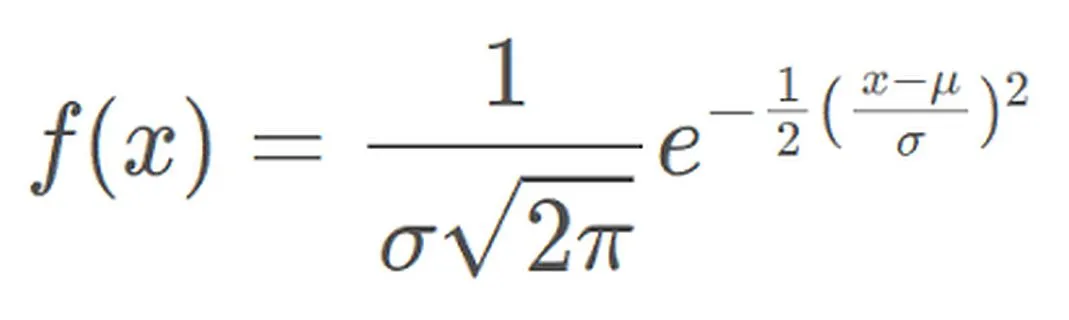
機率密度函數表示在給定值x附近的單位區間內常態分佈的隨機變數取值的機率密度。其中，μ表示平均值，σ表示標準差
常態分佈在實際中的應用是廣泛的。例如，人的身高和體重分佈近似於常態分佈。此外，考試成績通常呈常態分佈，高分和低分的人數較少，而中間分數的人數較多。這種分佈模式在許多領域都有重要的應用價值
2. 伯努利分佈
伯努利分佈（Bernoulli Distribution）是一種離散型機率分佈，用於描述只有兩種可能結果的單次隨機試驗。伯努利試驗可以是正面或反面，成功或失敗，是或否等。例如，拋硬幣、檢測產品是否合格、某人是否購買某種產品等。
伯努利分佈的機率品質函數為：
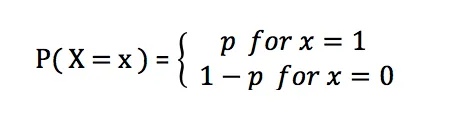
#在伯努利分佈中，p表示成功的機率，其取值範圍為0到1。當p等於0.5時，伯努利分佈就趨近於均勻分佈
伯努利分佈在實際中的應用：例如二項分佈就是伯努利分佈的n次獨立重複試驗。
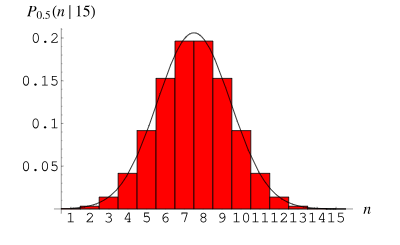
3. 二項分佈
二項分佈（Binomial Distribution）是一種離散型機率分佈，用於描述在n次獨立重複試驗中成功次數的機率分佈。每次試驗只有兩種可能的結果：成功（記為1）或失敗（記為0）。成功的機率為p，失敗的機率為1-p。
二項分佈的機率品質函數可以表示為：
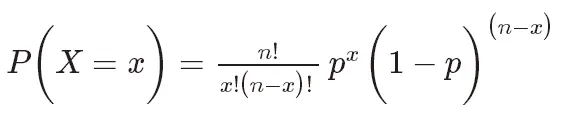
其中，P(X=k)表示成功次數為k的機率，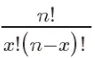
是組合數，表示從n次試驗中選擇k次成功的組合數。 p是成功的機率，取值範圍在0和1之間。 n是試驗次數。
二項分佈在實際中的應用非常廣泛。舉例來說，在醫學研究中，我們可以利用二項分佈來計算患者接受某種治療的成功率。在工程領域中，我們可以使用二項分佈來評估產品在生產過程中的合格率。這些都是二項分佈在實際應用中的重要例子
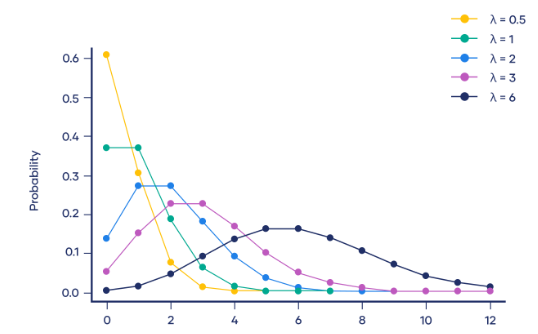
4. 泊松分佈
泊松分佈（Poisson Distribution）是一種離散型機率分佈，用於描述在固定時間內，事件發生的次數的機率分佈。泊松分佈適用於那些事件相互獨立，且平均發生速率恆定的情況。
泊松分佈的機率密度函數是：
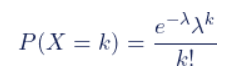
在這裡，P(X=k)代表在固定時間內事件發生k次的機率，λ表示事件的平均發生速率，也就是單位時間內事件發生的平均次數。 e是自然常數，約等於2.718。 k表示事件發生的次數
泊松分佈在實際中的應用十分廣泛，例如在電話呼叫中心，每分鐘打進的電話數量可以看作是泊松分佈，其中平均每分鐘打進的電話數為λ
5. 指數分佈
指數分佈（Exponential Distribution）是一種連續型機率分佈，用來描述在固定時間內，事件發生的機率。指數分佈適用於那些事件相互獨立，且平均發生速率恆定的情況。
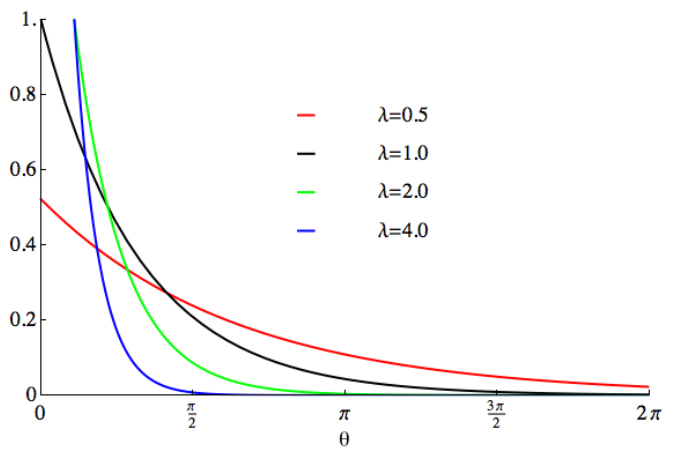
指數分佈的機率密度函數為：
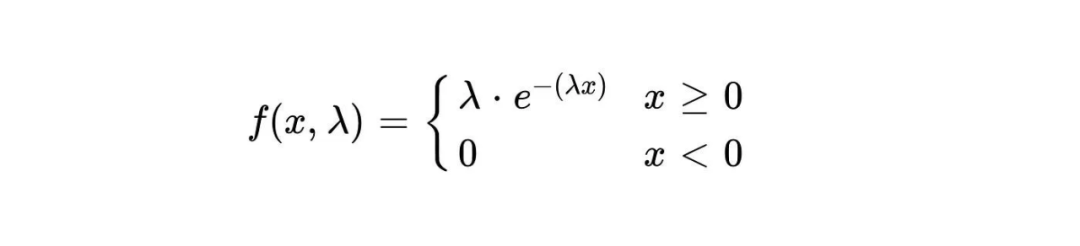
#在給定時間x內事件發生的機率密度用f(x,λ)表示。 λ表示事件的平均發生速率，即單位時間內事件發生的平均次數。 e是自然常數，約等於2.718
指數分佈在現實生活中有許多應用。例如，在放射性衰變中，放射性原子核的衰變時間可以被視為指數分佈。這意味著衰變時間的機率分佈符合指數函數。而平均衰變時間則對應著指數函數的參數λ
6. 伽瑪分佈
#Gamma分佈是一種連續機率分佈，用來描述事件在給定時間內發生的機率。它適用於事件之間互相獨立，且平均發生速率始終不變的情況
##在此其中，f(x)代表在特定時間x內事件發生的機率密度。 α和β是伽瑪分佈的形狀參數和速率參數。 α用來決定伽瑪分佈的形狀，取值範圍為0到正無窮。 β表示事件的平均發生速率，即在單位時間內事件發生的平均次數，取值範圍為0到正無窮。 e為自然常數，約等於2.718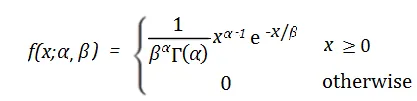
伽瑪分佈在實際中的應用：例如放射性衰變：在放射性衰變中，放射性原子核衰變的時間可以看作是伽瑪分佈，平均衰變時間即為β/α。
7. 貝塔分佈
貝塔分佈（Beta distribution）是一種連續型機率分佈，用來描述一組數值中成功次數的機率分佈。它有兩個參數，分別表示成功機率的期望值（mean）和標準差（standard deviation）。
貝塔分佈的機率密度函數如下：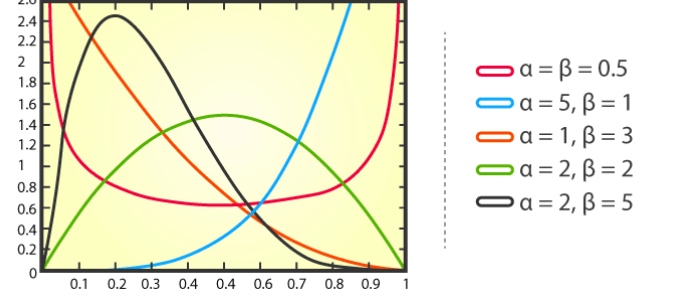
#在這其中，x代表成功的次數，α和β分別代表分佈的形狀參數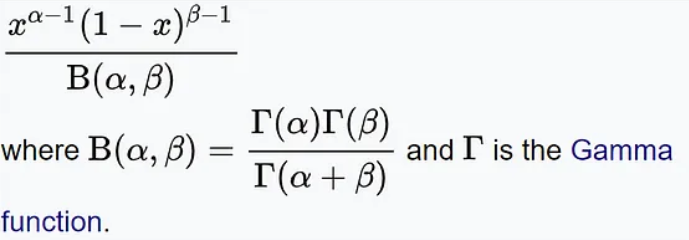
貝塔分佈在許多實際問題中都有應用。例如，在基因編輯中，研究人員可能會使用貝塔分佈來預測基因編輯技術成功編輯某個目標位點的機率。在金融領域，貝塔分佈可以用來描述資產價格的波動性，或者用於計算投資組合的預期收益
8. 均勻分佈
#均勻分佈是一種機率分佈，使用於描述一組數值在某區間內均勻分佈。均勻分佈有兩種：離散均勻分佈和連續均勻分佈。
離散均勻分佈：當一個離散隨機變數X滿足以下機率分佈：P(X=k) = k/(n 1)，其中k為非負整數，n為區間內的整數，我們稱X服從離散均勻分佈。連續均勻分佈：當一個連續隨機變數X的機率密度函數為f(x) = 1/(b-a)時，我們稱X服從連續均勻分佈，其中a和b為區間的兩個端點
均勻分佈的特徵是，在給定的區間內，每個數值都有相同的機會出現。例如，拋一枚公正的硬幣，正面和反面出現的機率都是1/2，這就是一種均勻分佈。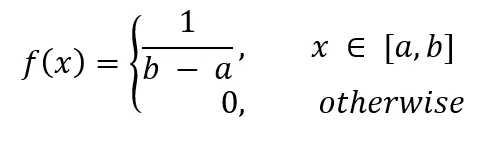 
9. 對數常態分佈
對數常態分佈（Log-normal distribution）是一種連續型機率分佈，它的特徵是隨機變數的對數服從常態分佈。換句話說，如果一個隨機變數X的對數ln(X)服從常態分佈，那麼這個隨機變數X就服從對數常態分佈。
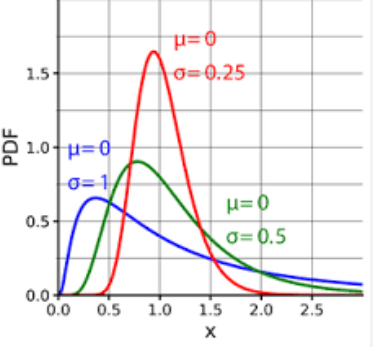
對數常態分佈的機率密度函數可以表示為：
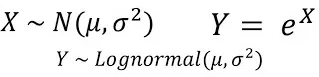
其中，μ是對數正態分佈的平均值，σ是對數常態分佈的標準差。
對數常態分佈在許多實際應用中都有重要意義，例如金融領域（股票價格、收益率等）、生物學（生長速率等）、經濟學（消費支出等）等。
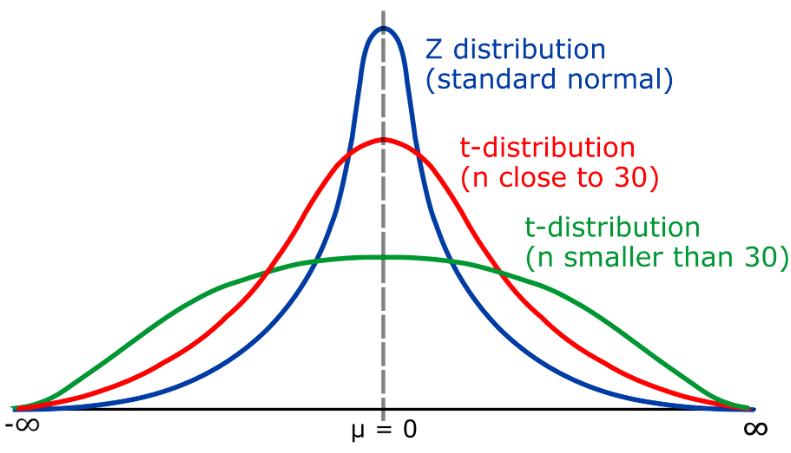
10. T分佈
T分佈，是一種連續型機率分佈，主要用於小樣本情況下描述平均值的分佈。 t分佈與常態分佈（Normal distribution）類似，但它的尾部可以向左右延伸，取決於自由度（k）的大小。 t分佈廣泛應用於統計推斷，例如在假設檢定中用於評估樣本平均值與總體平均值之間的顯著性差異。
t分佈的期望與變異數如下：
E(t)=0
#要重寫的內容是：Var( t)=k/(k-1)
t分佈的自由度（k）表示樣本大小（n）和總體標準差之間的關係。當k > 30時，t分佈接近常態分佈；當k接近1時，t分佈變為柯西分佈（Cauchy分佈）
在實際應用中，當樣本量較大（n>30 ）時，可以使用常態分佈進行假設檢驗，這時可以利用z統計量建立信賴區間。然而，當樣本量較小（n
11. Weibull分佈
Weibull分佈（Weibull distribution）是一種連續型機率分佈。
Weibull分佈的機率密度函數為：
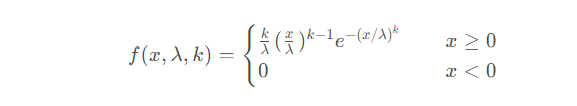
在韋伯分佈中，x視為隨機變量，λ則稱為比例參數(scale )，k則是形狀參數(shape)。就韋伯分佈而言，當k等於1時，它就是指數分佈。如果λ等於1的話，這就是最小化的韋伯分佈
以上是11個基本分佈，資料科學家95%的時間都在使用的詳細內容。更多資訊請關注PHP中文網其他相關文章！
