探討尋路演算法及程式碼實現的線路規劃解析

尋路演算法是電腦圖形學和人工智慧領域中常用的演算法之一,用於計算從一個點到另一個點的最短路徑或最優路徑。在本文中,我將詳細介紹兩種常用的尋路演算法:Dijkstra演算法和A*演算法
#Dijkstra演算法
##Dijkstra演算法是一種用於尋找圖中兩點之間最短路徑的廣度優先搜尋演算法。它的工作原理如下:
我們需要建立一個集合S來存放已經找到最短路徑的頂點
我們需要建立一個集合Q ,用來存放尚未找到最短路徑的頂點
在初始化距離數組dist時,需要將起始點到其他點的距離設為無窮大,而起始點到自身的距離則設為0
不斷重複下列步驟,直到集合Q為空:
- 在集合Q中找到距離起始點最近的頂點u,並將其加入集合S。
- 對於頂點u的每個鄰居頂點v,更新起始點到v的距離dist[v],如果dist[v] > dist[u] edge(u, v) ,則更新dist[v]為dist[u] edge(u, v)。
最終,dist數組中儲存的是從起始點到各個頂點的最短路徑
以下是用C#寫的Dijkstra演算法的原始碼:
class DijkstraAlgorithm
{
private int[,] graph;
private int size;
public DijkstraAlgorithm(int[,] graph)
{
this.graph = graph;
this.size = graph.GetLength(0);
}
public int[] FindShortestPath(int start, int end)
{
int[] dist = new int[size];
bool[] visited = new bool[size];
for (int i = 0; i <h4>A演算法<span></span>
</h4><p>#A演算法是一種啟發式搜尋演算法,用於尋找圖中兩點之間的最短路徑。演算法的想法如下:<span></span></p><p>建立一個存放待探索頂點的優先隊列openSet<span></span></p><p>我們需要建立一個名為gScore 的陣列,用於儲存從起始點到每個頂點的實際代價<span></span></p><p>我們需要建立一個名為fScore的數組,用於儲存從起始點到達目標點的估計代價<span> </span></p><p>將起始點加入openSet,並將gScore[start]設為0,fScore[start]設為起始點到目標點的估計代價<span></span></p><p>重複以下步驟,直到openSet為空:<span></span></p>- 在openSet中找到fScore最小的頂點current。
- 如果current等於目標點,表示已經找到最短路徑,返迴路徑。
- 將current從openSet中移除。
- 對於current的每個鄰居頂點neighbor,計算從起始點到neighbor的實際代價tempGScore,如果tempGScore小於gScore[neighbor],更新gScore[neighbor]為tempGScore,併計算fScore[neighbor] = gScore[neighbor] 估計代價。如果neighbor不在openSet中,將其加入openSet。
如果openSet為空,表示無法到達目標點,傳回空值
以下是用Java寫的A*演算法的原始碼:
import java.util.*;class AStarAlgorithm {private int[][] graph;private int size;public AStarAlgorithm(int[][] graph) {this.graph = graph;this.size = graph.length;}public List<integer> findShortestPath(int start, int end) {PriorityQueue<node> openSet = new PriorityQueue();int[] gScore = new int[size];int[] fScore = new int[size];int[] cameFrom = new int[size];boolean[] visited = new boolean[size];Arrays.fill(gScore, Integer.MAX_VALUE);Arrays.fill(fScore, Integer.MAX_VALUE);Arrays.fill(cameFrom, -1);gScore[start] = 0;fScore[start] = heuristicCostEstimate(start, end);openSet.offer(new Node(start, fScore[start]));while (!openSet.isEmpty()) {int current = openSet.poll().index;if (current == end) {return reconstructPath(cameFrom, current);}visited[current] = true;for (int neighbor = 0; neighbor reconstructPath(int[] cameFrom, int current) {List<integer> path = new ArrayList();path.add(current);while (cameFrom[current] != -1) {current = cameFrom[current];path.add(0, current);}return path;}private class Node implements Comparable<node> {public int index;public int fScore;public Node(int index, int fScore) {this.index = index;this.fScore = fScore;}@Overridepublic int compareTo(Node other) {return Integer.compare(this.fScore, other.fScore);}@Overridepublic boolean equals(Object obj) {if (this == obj) {return true;}if (obj == null || getClass() != obj.getClass()) {return false;}Node other = (Node) obj;return index == other.index;}@Overridepublic int hashCode() {return Objects.hash(index);}}}</node></integer></node></integer>以上是Dijkstra演算法和A*演算法的詳細介紹,包括演算法思維、流程和使用C#或Java實作的原始碼。這兩種演算法都是常用的尋路演算法,可以根據具體需求選擇使用。 當然在現在的城市裡導航軟體軟體可以給我們規劃好。
以上是探討尋路演算法及程式碼實現的線路規劃解析的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 最佳AI藝術生成器(免費付款)創意項目
Apr 02, 2025 pm 06:10 PM
最佳AI藝術生成器(免費付款)創意項目
Apr 02, 2025 pm 06:10 PM
本文回顧了AI最高的藝術生成器,討論了他們的功能,對創意項目的適用性和價值。它重點介紹了Midjourney是專業人士的最佳價值,並建議使用Dall-E 2進行高質量的可定製藝術。
 開始使用Meta Llama 3.2 -Analytics Vidhya
Apr 11, 2025 pm 12:04 PM
開始使用Meta Llama 3.2 -Analytics Vidhya
Apr 11, 2025 pm 12:04 PM
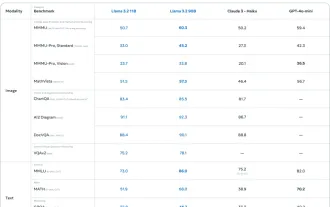
Meta的Llama 3.2:多模式和移動AI的飛躍 Meta最近公佈了Llama 3.2,這是AI的重大進步,具有強大的視覺功能和針對移動設備優化的輕量級文本模型。 以成功為基礎
 最佳AI聊天機器人比較(Chatgpt,Gemini,Claude&amp;更多)
Apr 02, 2025 pm 06:09 PM
最佳AI聊天機器人比較(Chatgpt,Gemini,Claude&amp;更多)
Apr 02, 2025 pm 06:09 PM
本文比較了諸如Chatgpt,Gemini和Claude之類的頂級AI聊天機器人,重點介紹了其獨特功能,自定義選項以及自然語言處理和可靠性的性能。
 Chatgpt 4 o可用嗎?
Mar 28, 2025 pm 05:29 PM
Chatgpt 4 o可用嗎?
Mar 28, 2025 pm 05:29 PM
Chatgpt 4當前可用並廣泛使用,與諸如ChatGpt 3.5(例如ChatGpt 3.5)相比,在理解上下文和產生連貫的響應方面取得了重大改進。未來的發展可能包括更多個性化的間
 頂級AI寫作助理來增強您的內容創建
Apr 02, 2025 pm 06:11 PM
頂級AI寫作助理來增強您的內容創建
Apr 02, 2025 pm 06:11 PM
文章討論了Grammarly,Jasper,Copy.ai,Writesonic和Rytr等AI最高的寫作助手,重點介紹了其獨特的內容創建功能。它認為Jasper在SEO優化方面表現出色,而AI工具有助於保持音調的組成
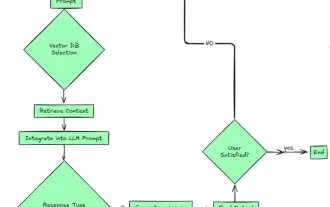 構建AI代理的前7個代理抹布系統
Mar 31, 2025 pm 04:25 PM
構建AI代理的前7個代理抹布系統
Mar 31, 2025 pm 04:25 PM
2024年見證了從簡單地使用LLM進行內容生成的轉變,轉變為了解其內部工作。 這種探索導致了AI代理的發現 - 自主系統處理任務和最少人工干預的決策。 Buildin
 選擇最佳的AI語音生成器:評論的頂級選項
Apr 02, 2025 pm 06:12 PM
選擇最佳的AI語音生成器:評論的頂級選項
Apr 02, 2025 pm 06:12 PM
本文評論了Google Cloud,Amazon Polly,Microsoft Azure,IBM Watson和Discript等高級AI語音生成器,重點介紹其功能,語音質量和滿足不同需求的適用性。
 AV字節:Meta&#039; llama 3.2,Google的雙子座1.5等
Apr 11, 2025 pm 12:01 PM
AV字節:Meta&#039; llama 3.2,Google的雙子座1.5等
Apr 11, 2025 pm 12:01 PM
本週的AI景觀:進步,道德考慮和監管辯論的旋風。 OpenAI,Google,Meta和Microsoft等主要參與者已經釋放了一系列更新,從開創性的新車型到LE的關鍵轉變






