揭秘的全新版本:你從未見過的Transformer數學原理
近日,arxiv 上發布了一篇論文,對 Transformer 的數學原理進行全新解讀,內容很長,知識很多,十二分建議閱讀原文。

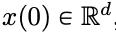 在時間間隔 (0,T) 上會依照給定的時變速度場
在時間間隔 (0,T) 上會依照給定的時變速度場 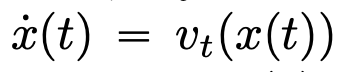 進行演化。因此,DNN 可以看成是從一個
進行演化。因此,DNN 可以看成是從一個 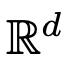 到另一個
到另一個 的流映射(Flow Map)
的流映射(Flow Map)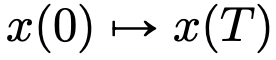 。即使在經典 DNN 架構限制下的速度場
。即使在經典 DNN 架構限制下的速度場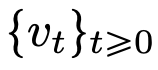 中,流映射之間也具有強烈的相似性。
中,流映射之間也具有強烈的相似性。 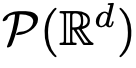 上的流映射,即 d 維概率測度空間(the space of probability measures)間的映射。為了實現這種在度量空間間進行轉換的流映射,Transformers 需要建立了一個平均場相互作用的粒子系統(mean-field interacting particle system.)。
上的流映射,即 d 維概率測度空間(the space of probability measures)間的映射。為了實現這種在度量空間間進行轉換的流映射,Transformers 需要建立了一個平均場相互作用的粒子系統(mean-field interacting particle system.)。 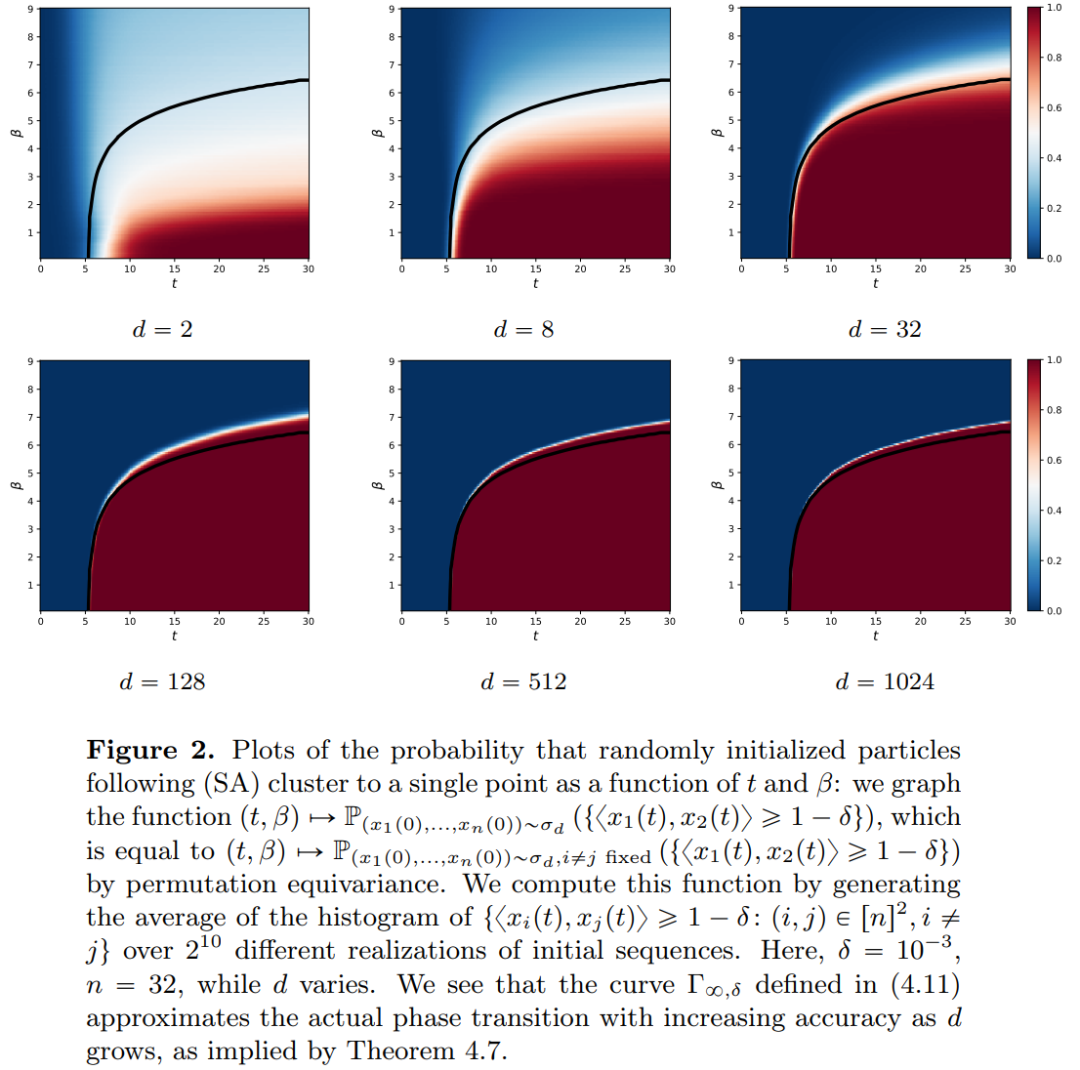
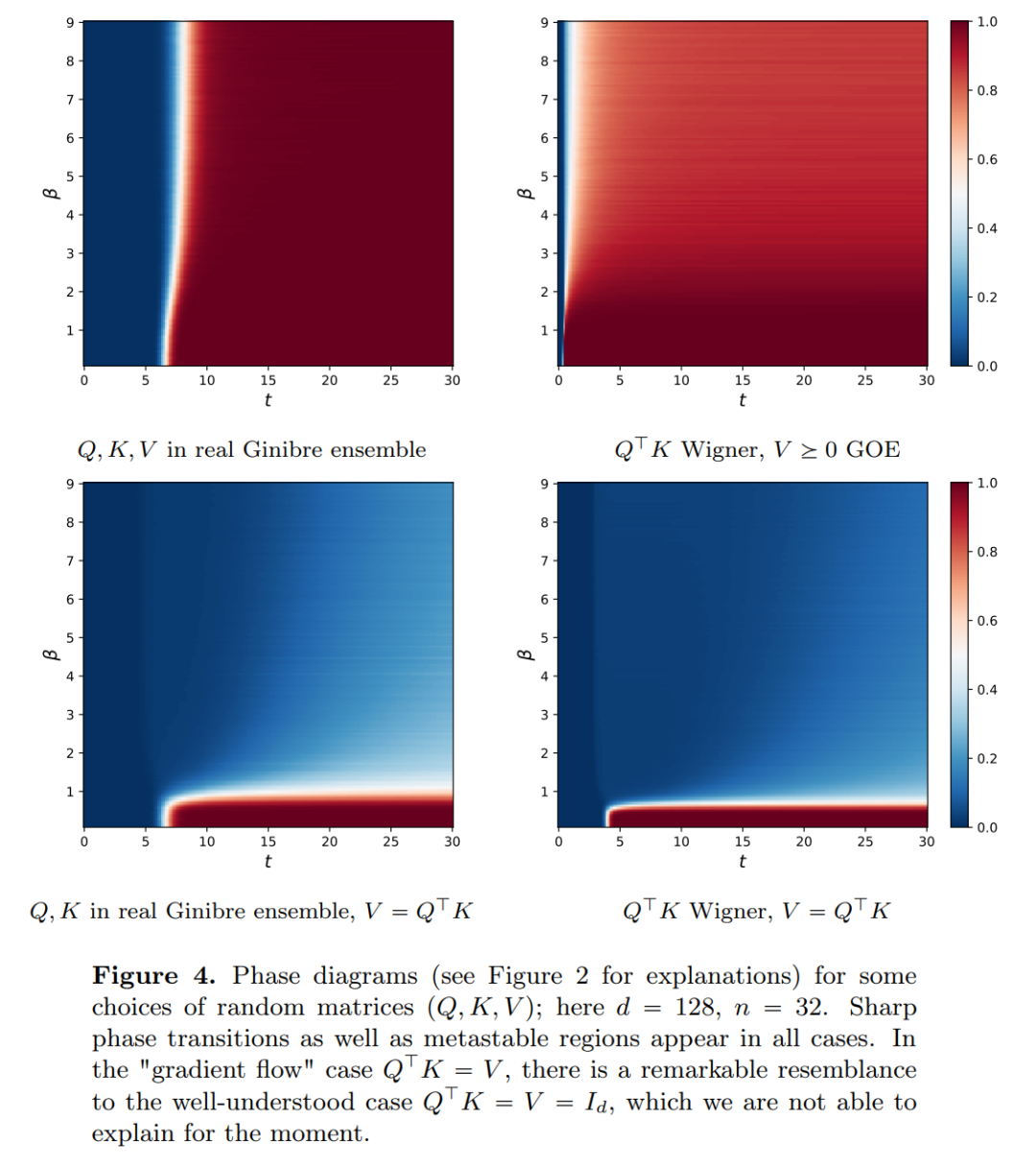

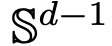 的空間內部,而自註意力機制則是透過經驗度量實現粒子之間的非線性耦合。反過來,經驗測量根據連續性偏微分方程進行演化。本文也為自註意引入了一個更簡單好用的替代模型,一個能量函數的 Wasserstein 梯度流,而能量函數在球面上點的最適配置已經有成熟的研究方法。
的空間內部,而自註意力機制則是透過經驗度量實現粒子之間的非線性耦合。反過來,經驗測量根據連續性偏微分方程進行演化。本文也為自註意引入了一個更簡單好用的替代模型,一個能量函數的 Wasserstein 梯度流,而能量函數在球面上點的最適配置已經有成熟的研究方法。 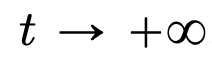 時聚成一個點。研究者對粒子集群收縮率的精確描述對此結果進行了補充說明。具體來說,研究者繪製了所有粒子間距離的直方圖,以及所有粒子快要完成聚類的時間點(見原文第 4 節)。研究者還在不假設維數 d 較大的情況下就得到了聚類結果(見原文第 5 節)。
時聚成一個點。研究者對粒子集群收縮率的精確描述對此結果進行了補充說明。具體來說,研究者繪製了所有粒子間距離的直方圖,以及所有粒子快要完成聚類的時間點(見原文第 4 節)。研究者還在不假設維數 d 較大的情況下就得到了聚類結果(見原文第 5 節)。 以上是揭秘的全新版本:你從未見過的Transformer數學原理的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 突破傳統缺陷檢測的界限,\'Defect Spectrum\'首次實現超高精度豐富語意的工業缺陷檢測。
Jul 26, 2024 pm 05:38 PM
突破傳統缺陷檢測的界限,\'Defect Spectrum\'首次實現超高精度豐富語意的工業缺陷檢測。
Jul 26, 2024 pm 05:38 PM
在現代製造業中,精準的缺陷檢測不僅是確保產品品質的關鍵,更是提升生產效率的核心。然而,現有的缺陷檢測資料集常常缺乏實際應用所需的精確度和語意豐富性,導致模型無法辨識特定的缺陷類別或位置。為了解決這個難題,由香港科技大學廣州和思謀科技組成的頂尖研究團隊,創新地開發了「DefectSpectrum」資料集,為工業缺陷提供了詳盡、語義豐富的大規模標註。如表一所示,相較於其他工業資料集,「DefectSpectrum」資料集提供了最多的缺陷標註(5438張缺陷樣本),最細緻的缺陷分類(125個缺陷類別
 數百萬晶體資料訓練,解決晶體學相位問題,深度學習方法PhAI登Science
Aug 08, 2024 pm 09:22 PM
數百萬晶體資料訓練,解決晶體學相位問題,深度學習方法PhAI登Science
Aug 08, 2024 pm 09:22 PM
編輯|KX時至今日,晶體學所測定的結構細節和精度,從簡單的金屬到大型膜蛋白,是任何其他方法都無法比擬的。然而,最大的挑戰——所謂的相位問題,仍然是從實驗確定的振幅中檢索相位資訊。丹麥哥本哈根大學研究人員,開發了一種解決晶體相問題的深度學習方法PhAI,利用數百萬人工晶體結構及其相應的合成衍射數據訓練的深度學習神經網絡,可以產生準確的電子密度圖。研究表明,這種基於深度學習的從頭算結構解決方案方法,可以以僅2埃的分辨率解決相位問題,該分辨率僅相當於原子分辨率可用數據的10%到20%,而傳統的從頭算方
 英偉達對話模式ChatQA進化到2.0版本,上下文長度提到128K
Jul 26, 2024 am 08:40 AM
英偉達對話模式ChatQA進化到2.0版本,上下文長度提到128K
Jul 26, 2024 am 08:40 AM
開放LLM社群正是百花齊放、競相爭鳴的時代,你能看到Llama-3-70B-Instruct、QWen2-72B-Instruct、Nemotron-4-340B-Instruct、Mixtral-8x22BInstruct-v0.1等許多表現優良的模型。但是,相較於以GPT-4-Turbo為代表的專有大模型,開放模型在許多領域仍有明顯差距。在通用模型之外,也有一些專精關鍵領域的開放模型已被開發出來,例如用於程式設計和數學的DeepSeek-Coder-V2、用於視覺-語言任務的InternVL
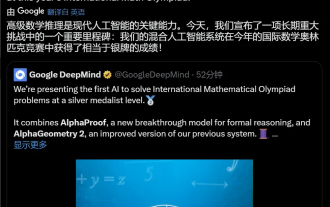 GoogleAI拿下IMO奧數銀牌,數學推理模型AlphaProof面世,強化學習 is so back
Jul 26, 2024 pm 02:40 PM
GoogleAI拿下IMO奧數銀牌,數學推理模型AlphaProof面世,強化學習 is so back
Jul 26, 2024 pm 02:40 PM
對AI來說,奧數不再是問題了。本週四,GoogleDeepMind的人工智慧完成了一項壯舉:用AI做出了今年國際數學奧林匹克競賽IMO的真題,並且距拿金牌僅一步之遙。上週剛結束的IMO競賽共有六道賽題,涉及代數、組合學、幾何和數論。谷歌提出的混合AI系統做對了四道,獲得28分,達到了銀牌水準。本月初,UCLA終身教授陶哲軒剛剛宣傳了百萬美元獎金的AI數學奧林匹克競賽(AIMO進步獎),沒想到7月還沒過,AI的做題水平就進步到了這種水平。 IMO上同步做題,做對了最難題IMO是歷史最悠久、規模最大、最負
 arXiv論文可以發「彈幕」了,史丹佛alphaXiv討論平台上線,LeCun按讚
Aug 01, 2024 pm 05:18 PM
arXiv論文可以發「彈幕」了,史丹佛alphaXiv討論平台上線,LeCun按讚
Aug 01, 2024 pm 05:18 PM
乾杯!當論文討論細緻到詞句,是什麼體驗?最近,史丹佛大學的學生針對arXiv論文創建了一個開放討論論壇——alphaXiv,可以直接在任何arXiv論文之上發布問題和評論。網站連結:https://alphaxiv.org/其實不需要專門訪問這個網站,只需將任何URL中的arXiv更改為alphaXiv就可以直接在alphaXiv論壇上打開相應論文:可以精準定位到論文中的段落、句子:右側討論區,使用者可以發表問題詢問作者論文想法、細節,例如:也可以針對論文內容發表評論,例如:「給出至
 PRO | 為什麼基於 MoE 的大模型更值得關注?
Aug 07, 2024 pm 07:08 PM
PRO | 為什麼基於 MoE 的大模型更值得關注?
Aug 07, 2024 pm 07:08 PM
2023年,幾乎AI的每個領域都在以前所未有的速度進化,同時,AI也不斷地推動著具身智慧、自動駕駛等關鍵賽道的技術邊界。在多模態趨勢下,Transformer作為AI大模型主流架構的局面是否會撼動?為何探索基於MoE(專家混合)架構的大模型成為業界新趨勢?大型視覺模型(LVM)能否成為通用視覺的新突破? ……我們從過去的半年發布的2023年本站PRO會員通訊中,挑選了10份針對以上領域技術趨勢、產業變革進行深入剖析的專題解讀,助您在新的一年裡為大展宏圖做好準備。本篇解讀來自2023年Week50
 為大模型提供全新科學複雜問答基準與評估體系,UNSW、阿貢、芝加哥大學等多家機構共同推出SciQAG框架
Jul 25, 2024 am 06:42 AM
為大模型提供全新科學複雜問答基準與評估體系,UNSW、阿貢、芝加哥大學等多家機構共同推出SciQAG框架
Jul 25, 2024 am 06:42 AM
編輯|ScienceAI問答(QA)資料集在推動自然語言處理(NLP)研究中發揮著至關重要的作用。高品質QA資料集不僅可以用於微調模型,也可以有效評估大語言模型(LLM)的能力,尤其是針對科學知識的理解和推理能力。儘管目前已有許多科學QA數據集,涵蓋了醫學、化學、生物等領域,但這些數據集仍有一些不足之處。其一,資料形式較為單一,大多數為多項選擇題(multiple-choicequestions),它們易於進行評估,但限制了模型的答案選擇範圍,無法充分測試模型的科學問題解答能力。相比之下,開放式問答
 準確率達60.8%,浙大基於Transformer的化學逆合成預測模型,登Nature子刊
Aug 06, 2024 pm 07:34 PM
準確率達60.8%,浙大基於Transformer的化學逆合成預測模型,登Nature子刊
Aug 06, 2024 pm 07:34 PM
編輯|KX逆合成是藥物發現和有機合成中的關鍵任務,AI越來越多地用於加快這一過程。現有AI方法性能不盡人意,多樣性有限。在實踐中,化學反應通常會引起局部分子變化,反應物和產物之間存在很大重疊。受此啟發,浙江大學侯廷軍團隊提出將單步逆合成預測重新定義為分子串編輯任務,迭代細化目標分子串以產生前驅化合物。並提出了基於編輯的逆合成模型EditRetro,該模型可以實現高品質和多樣化的預測。大量實驗表明,模型在標準基準資料集USPTO-50 K上取得了出色的性能,top-1準確率達到60.8%。






