在推薦系統中，透過收集資料來訓練推薦模型，以向使用者推薦合適的物品。當使用者與推薦的物品互動時，收集的資料又會用於進一步訓練模型，形成一個閉環循環。然而，這個閉環中可能存在各種影響因素，導致誤差的產生。主要的誤差原因在於訓練模式所使用的數據大多是觀測數據，而非理想的訓練數據，受到曝光策略和使用者選擇等因素的影響。這種偏差的本質在於經驗風險估計的期望和真實理想風險估計的期望之間的差異。
推薦行銷系統裡面比較常見的偏差主要有以下三種：
還有其它一些偏差，例如位置偏差、一致性偏差等。
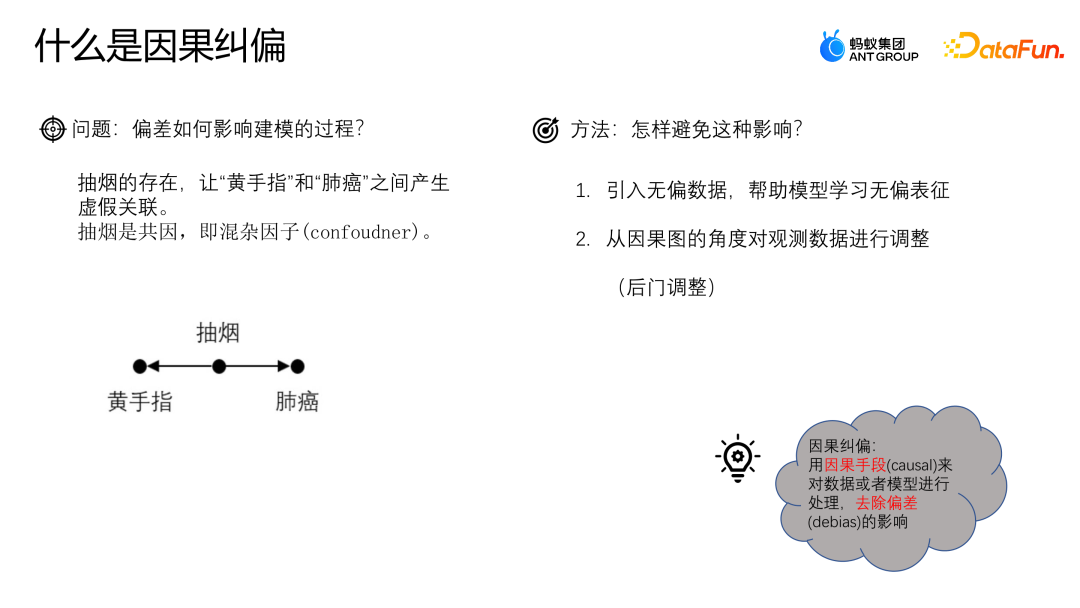
#下面透過一個例子來理解偏差對建模過程造成的影響。假設我們想研究咖啡飲用與心臟病之間的關係。我們發現咖啡飲用者更容易罹患心臟病，因此可能會得出結論咖啡飲用與心臟病有直接的因果關係。 然而，我們需要注意混雜因子的存在。例如，假設咖啡飲用者更可能也是吸煙者。吸煙本身就與心臟病有關。因此，我們不能簡單地將咖啡飲用與心臟病之間的關係歸因於因果關係，而是可能是由於吸菸這個混雜因子的存在所導致的。 為了更準確地研究咖啡飲用與心臟病之間的關係，我們需要控制吸菸的影響。一種方法是進行配對研究，即將吸煙者和非吸煙者進行配對，然後比較他們在咖啡飲用和心臟病之間的關係。這樣可以消除吸菸對結果的混雜影響。 因果關係是一個what if的問題，即在其他條件不變的情況下，改變咖啡飲用會不會導致心臟病發生的改變。只有在控制了混雜因子的影響後，才能更精確地判斷咖啡飲用與心臟病之間是否存在因果關係。
如何避免這種問題呢? 一種比較常見的方法就是引入無偏的數據，透過使用無偏的數據來幫助模型學習無偏的表徵；另外一種方法是從因果圖的角度出發，透過後期對觀測資料進行調整來進行糾偏。因果糾偏就是透過因果的手段對資料或模型進行處理，去除偏差的影響。
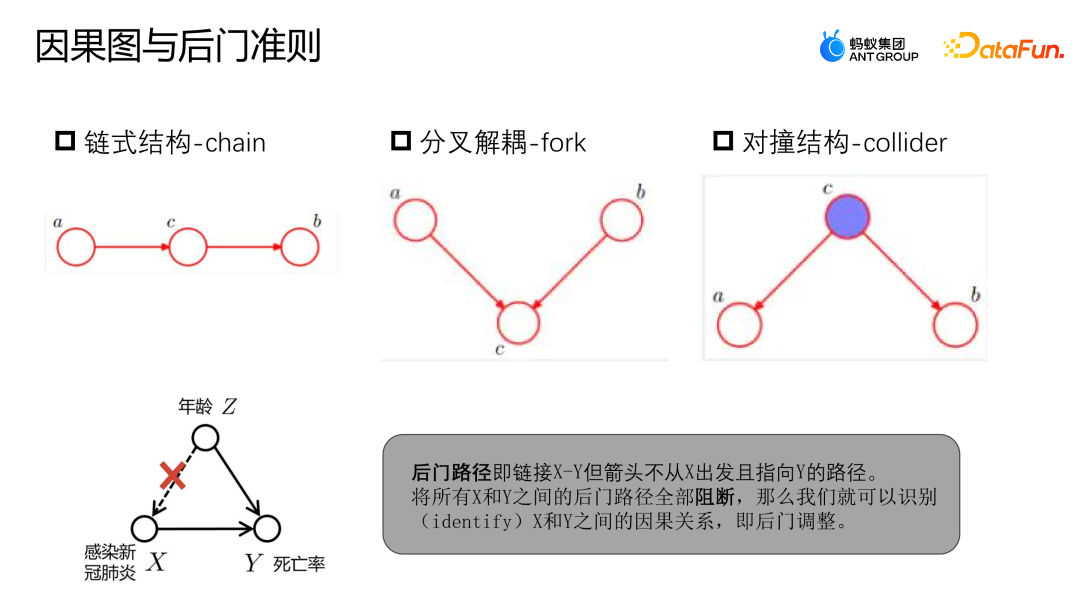
#因果圖是一個有向無環圖，用於描述場景中節點之間的因果關係。它由鍊式結構、分叉結構和對撞結構三個組成。
可以參考上圖的範例來決定後門路徑和後門準則。後門路徑是指連結X到Y的路徑，但是從Z出發最終指向了Y。與先前的例子類似，感染新冠肺炎與死亡率之間並不是純粹的因果關係。感染新冠肺炎受到年齡的影響，老年族群感染新冠肺炎的機率較高，而老年族群的死亡率也較高。然而，如果我們有足夠的數據，能夠將X和Y之間的後門路徑全部阻斷，即給定了Z，那麼X和Y就可以被建模為獨立的關係，這樣就可以得到真正的因果關係。
下面介紹螞蟻團隊基於資料融合糾偏的工作，目前已經發表在 SIGIR2023 的Industry Track 上。工作的想法是透過無偏資料來做資料增廣，指導模型的糾偏。
無偏資料整體跟有偏資料的分佈不相同，有偏資料會集中在整個樣本空間的某部分區域，缺少的樣本會集中在有偏數據相對較少的部分區域，所以增廣的樣本如果是靠近無偏區域比較多的區域，那無偏數據會發揮更多的作用；如果增廣樣本靠近有偏數據的區域，那有偏數據就會發揮更多的作用。對此這篇論文設計了 MDI 的模型，可以更好地利用無偏和有偏資料來做資料增廣。
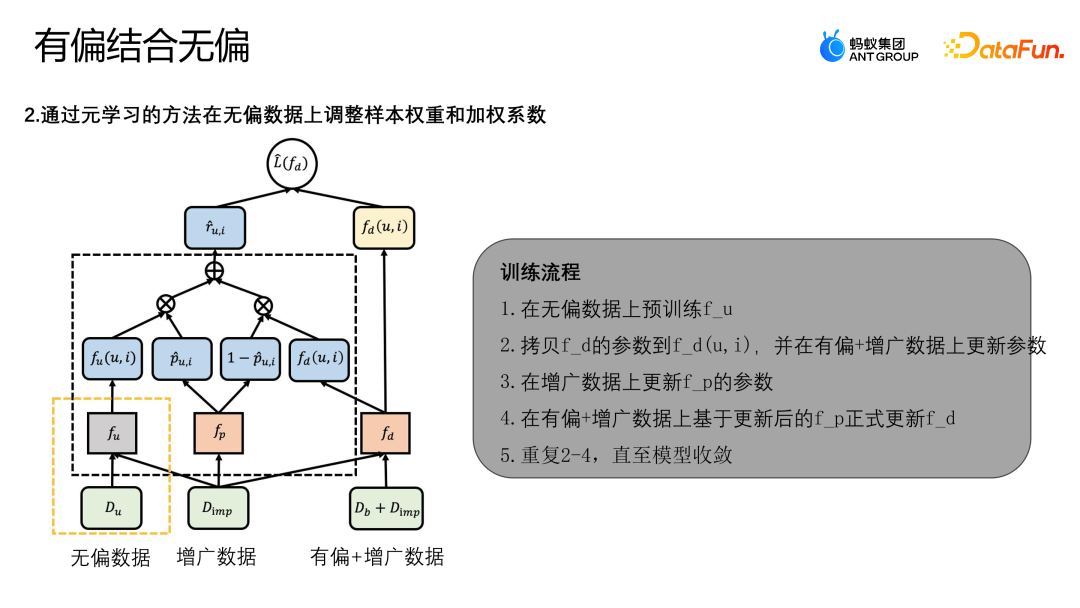
上圖中展示了演算法的框架圖，MDI 模型是透過元學習的方法，在無偏資料上調整樣本的權重以及加權的係數。首先，MDI 模型訓練有兩個階段：
透過優化L（fd） 的經營損失來訓練融合去偏模型fd，最終的Lose 損失主要有兩項，一個是L-IPS，一個是L -IMP。 L-IPS 是我們利用原始樣本來進行最佳化的一個IPS 模組；Ｒ-UI 是利用任意模型來求導傾向性分數（判斷樣本屬於無偏樣本的機率或屬於有偏樣本的機率）；第二項的L-IMP 是預設的增廣模組的權重，Ｒ-UI 是預設的增廣模組產生的尾標；P－UI 與１—Ｐ－UI 是無偏的Teacher 模型和融合模型在當前樣本的傾向分數；fp 就是用來學傾向性分數的一個函數，透過學習fp 自適應結合無偏資料的Teacher 模型與目前的有偏資料訓練的模型，共同為增廣樣本產生偽標記；透過這種方法來學習更複雜的pattern 訊息，fp 透過Meta learning 的方式求解。
以下是演算法完整的訓練流程：
##
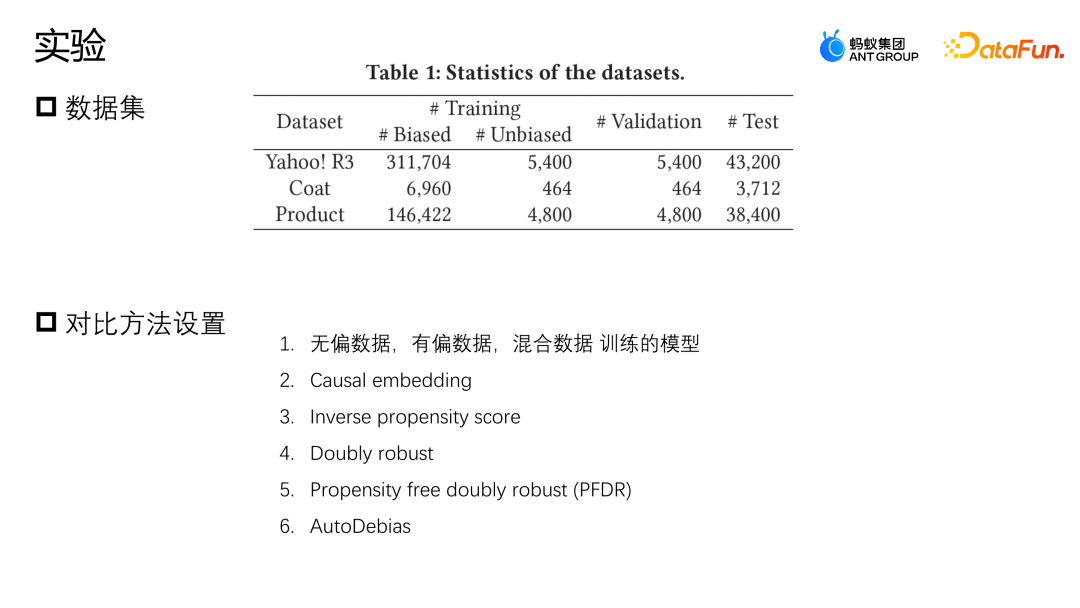
我們在 Yahoo R3 和 Coat 這兩個公開資料集上進行了評估。 Yahoo R3 透過收集 15000 用戶對 1000 首歌曲的評分，總共收集了 31 萬用戶對 1000 首歌曲的評分，總共收集了 31 萬個有偏數據
以及 5400 個無偏數據。 Coat 資料集是透過 290 個使用者對三百件衣服的評分收集了 6900 條有偏資料和 4600 個無偏資料。兩個資料集用戶的評分都在 1 到 5 之間，有偏的資料來自於平台的資料用戶，無偏的樣本是透過隨機給予使用者選擇評分的形式來收集。除了兩個公開的資料集，螞蟻還使用了業界實際場景的一個資料集，為了模擬無偏資料樣本非常少的情況，我們把全部的有偏資料和10% 的無偏資料用來訓練，保留10% 的無偏資料作為驗證，剩下80% 作為測試集。
我們使用的Baseline 對比的方法主要是以下幾種：第一個方法是分別利用無偏資料、單有偏資料和直接資料融合訓練的模型；第二個方法是透過少部分無偏數據，設計了一個正則性的表徵約束有偏數據、無偏數據表徵的相似度來進行糾偏的操作；第三個方法是逆概率權重的方法，傾向性分數的一個逆概率。 Double robust 也是一個比較常見的糾偏的方法；Propensity free double robust 是一個資料增廣的方法，它先用無偏的樣本學習一個增廣的模型，然後透過增廣的樣本幫助整個模型進行糾偏；Auto debias 也會用到一些無偏的資料做增廣來幫助模型糾偏。
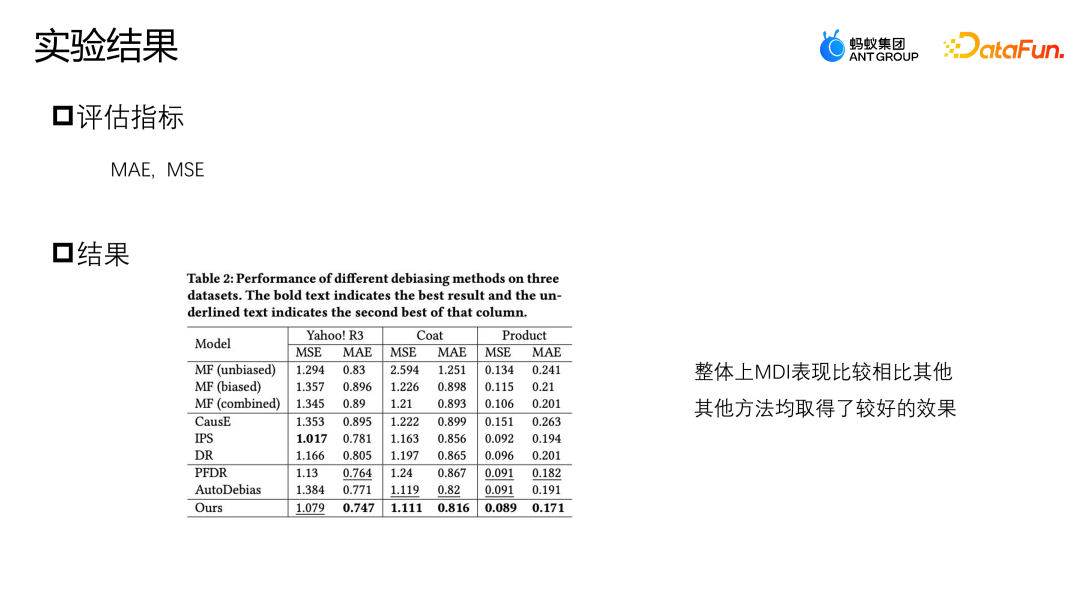
我們使用了 MSE 和 MAE 這兩個指標來評估表現。如圖所示，我們提出的 MDI 方法，在 Coat 以及 Product 兩個資料集上，兩個指標都有比較好的表現。
在 Yahoo R3 資料集上，我們提出的方法在 MAE 上的表現指標最好，在 MSE 除了 IPS 以外的方法表現是最好的。三種資料增廣的方法，PFDR、Auto Debias 以及我們提出的MDI，在多數情況下表現的都會更好，但是由於PFDR 是提前利用無偏資料訓練增廣模型，會嚴重依賴於無偏資料的質量，因此它在Coat 模型上就只有464 個無偏訓練資料樣本，當無偏樣本比較少的時候，它的增廣模組就會比較差，資料表現也會相對差一些。
AutoDebias 在不同資料上的表現與 PFDR 剛好相反。由於MDI 設計了同時利用無偏資料以及有偏資料的增廣方法，所以具有更強的資料增廣模組，因此它在無偏資料比較少或無偏資料比較充足這兩種情況下都可以獲得比較好的效果。
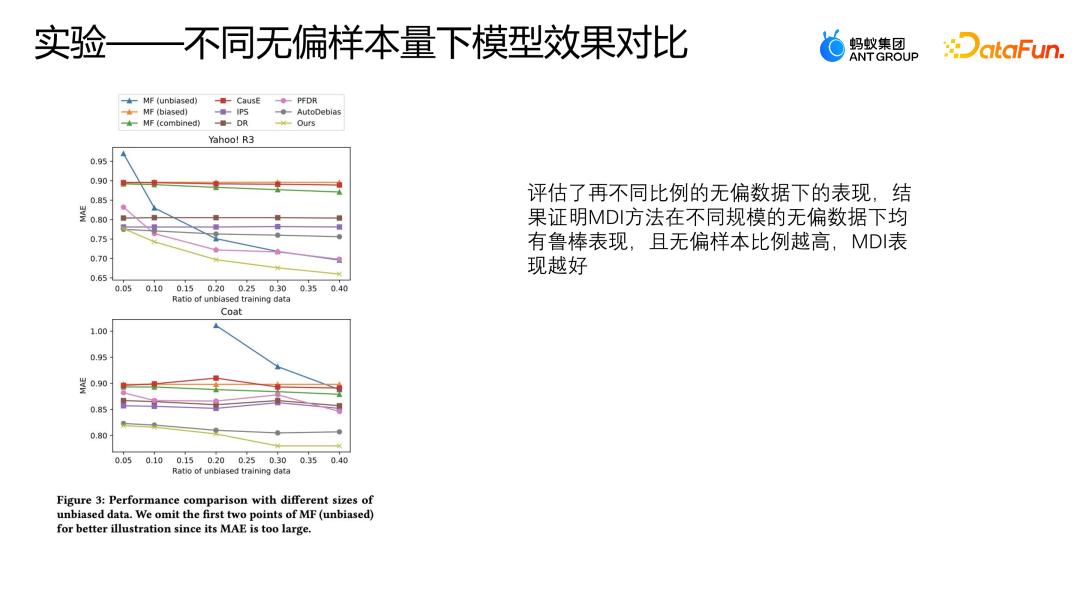
我們在兩個公開資料集上也評估了這些模型在不同比例的無偏資料下的表現，分別使用了50% 到40% 的無偏資料以及全部的有偏資料來用於訓練，其它邏輯與前面 10% 的無偏資料做驗證，剩下的資料做測試，這個設定與前面的實驗一樣。
上圖展示了採用不同方法在不同比例的無偏數據下的MAE 的表現，橫坐標表示無偏數據的比例，縱坐標表示各個方法在無偏數據上的效果，可以看到隨著無偏資料比例的增加AutoDebias、IPS 以及DoubleRubus 的MAE 沒有明顯的下降過程。但不按Debias 的方式，直接利用原始資料融合來學習的方法則會有比較明顯的下降，這是因為無偏資料的樣本比例越高，我們整體的資料品質就越好，所以模型可以學到更好的表現。 當 Yahoo R3 的資料使用超過 30% 的無偏資料來訓練的時候，
這種方式甚至超過了除 MDI 以外其它所有的糾偏方法。但 MDI 的方式相對來說可以獲得更好的表現，這也可以證明 MDI 方法在不同規模的無偏數據下都有比較穩健的結果。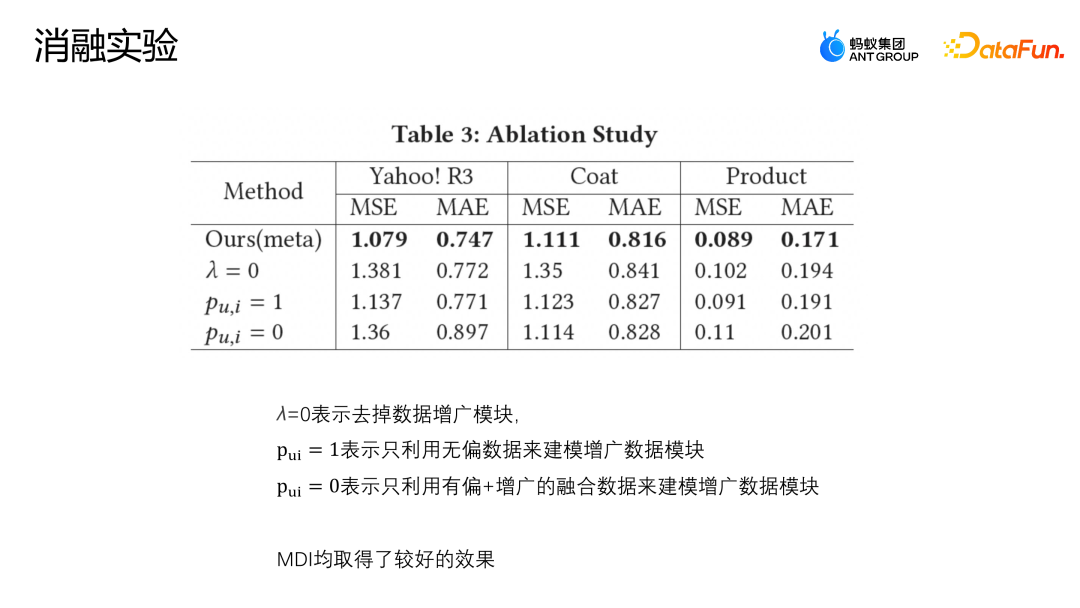
同時我們也進行了消融實驗，在三個資料集上分別驗證增廣模組當中各個部分的設定是否有效。 ######
λ=0 的設定表示直接去除了增廣模組；Pu,i = 1 表示只利用無偏資料建模增廣資料模組；Pu,i = 0 表示只利用有偏以及增廣的融合資料建模增廣資料模組。
上圖中展示了消融實驗的結果，可以看到 MDI 方法在三個資料集上都取得了比較好的效果，說明增廣模組是有必要的。
無論是在公開資料集上，或是實際業務場景的資料集上，我們提出的融合無偏和有偏資料的增廣方法相比之前已有的數據融合方案都有更好的效果，同時透過參數敏感度實驗以及消融實驗也驗證了MDI 的穩健性。
以下來介紹下團隊的另一個工作：基於後門調整糾偏。這項工作也已發表在了 SIGIR2023 的 Industry Track 上。後門調整糾偏應用的場景就是行銷推薦的場景，如下圖所示，用戶與優惠券或用戶與任意廣告、item 的交互是不受任何干預的，有均等的可能去任意交互，每張券也有均等的可能會曝光給任意用戶。
但在實際的業務場景當中，為了保護或幫助一些小商家提升流量，以及保證全局的使用者參與體驗，通常會設置一系列的策略約束，這種情況就會導致一部分用戶會更多的曝光某些優惠券，另一部分用戶會更多的曝光另外一張優惠券，這種幹預就是前文中提到的confounder。
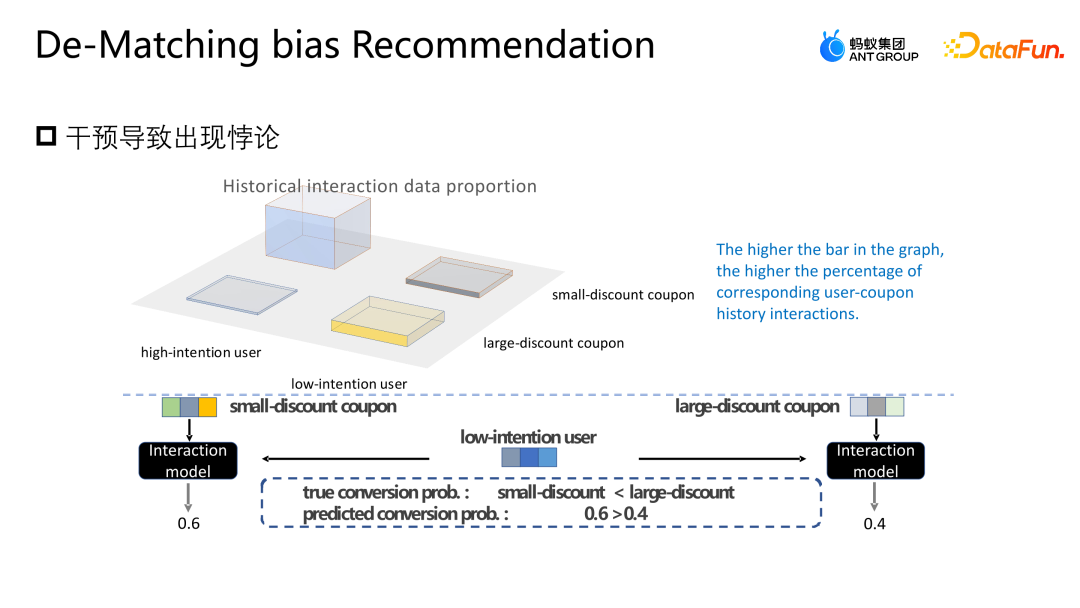
這種介入在電商行銷場景裡會產生什麼問題呢？如上圖所示，為了簡化，我們將用戶簡單地分為高參與意願和低參與意願兩類，將優惠券簡單地分為大折扣和小折扣兩類。圖中長條圖的高低表示了對應樣本的全局佔比，長條圖越高，表示對應樣本在整體訓練資料當中佔比越多。圖中所顯示的小折扣的優惠券以及高參與意願用戶樣本佔據了大多數，會導致模型學到圖中所示的分佈，模型會認為高參與意願用戶更喜歡小折扣的優惠券。但實際上面對同樣的使用門檻，用戶肯定會傾向於折扣更高的優惠券，這樣才會更省錢。圖中模型對於實際的轉換機率是小折扣優惠券低於大折扣優惠券的，但是模型對於某一個樣本的預估反而會認為小折扣優惠券核銷概率更高，所以模型也會推薦這個打分對應的優惠券，這就形成了一個悖論。
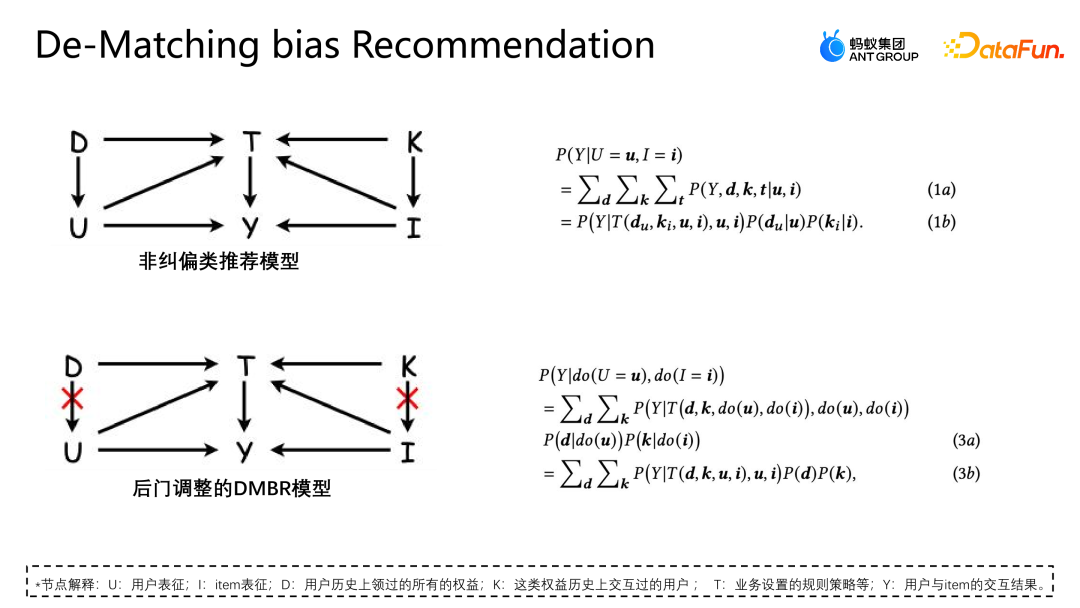
從因果圖的角度分析這個悖論產生的原因，在當前的場景下應用非糾偏的推薦模型，其因果圖構造如上圖所示，U 表示使用者的表徵，I 表示item 的表徵。 D 和K 分別是使用者視角與權益視角的歷史互動情況，T 表示目前業務設定的一些規則約束，T 是沒辦法直接量化的，但是我們可以透過D 和K 來間接地看出它對使用者和item的影響。 y 表示使用者與 item 的交互，結果就是 item 是否被點擊、被核銷等。
因果圖所代表的條件機率公式如圖右上所示，公式推導遵循貝葉斯機率公式。在給定U 和I 的條件下，最終求導P|Y ui 並不是只與U 和I 相關，因為U 會受到 du 的影響，也就是p 給定u 的時候 p（du）的機率也是存在的。在給定 I 的時候同理，I 也會受到 ki 的影響，而這個情況產生的原因是因為 D 和 K 的存在導致了場景當中存在後門路徑。也就是不從 U 出發，但是最終指向 y 的路徑（U-D-T-Y 或 I-K-T-Y 路徑）這種後門路徑會表示一個虛假觀念，也就是 U 不僅可以透過 T 影響 y，也可以透過 D 影響 y。
調整的方法是將D 到U 的路徑人為切斷，這樣U 只能透過U-T-Y 跟 U-Y直接影響y，這種方式可以去除虛假關聯，從而建模真正的因果關係。後門調整是對觀測資料做do-calculus，然後用do算子聚合所有D以及所有K的情況表現，避免U和I受到D和K的影響。透過這種方式建模一個真正的因果關係。這個公式的推導近似估計形式如下圖所示。
4a 和前面 3b 形式是一樣的，而 4b 則是做了樣本空間的近似。因為理論上來講 D 和 K 的樣本空間是無限的，只能透過收集到的資料（樣本空間的 D 和 K 取一個大小）來做近似。 4c 和 4d 都是期望的近似的推導，透過這種方式最終只需額外建模一個無偏表徵 T。 T 是透過遍歷所有情況下使用者跟 item 的表徵機率分佈和，額外建模無偏表徵 T，來幫助模型得到最終的無偏資料估計。
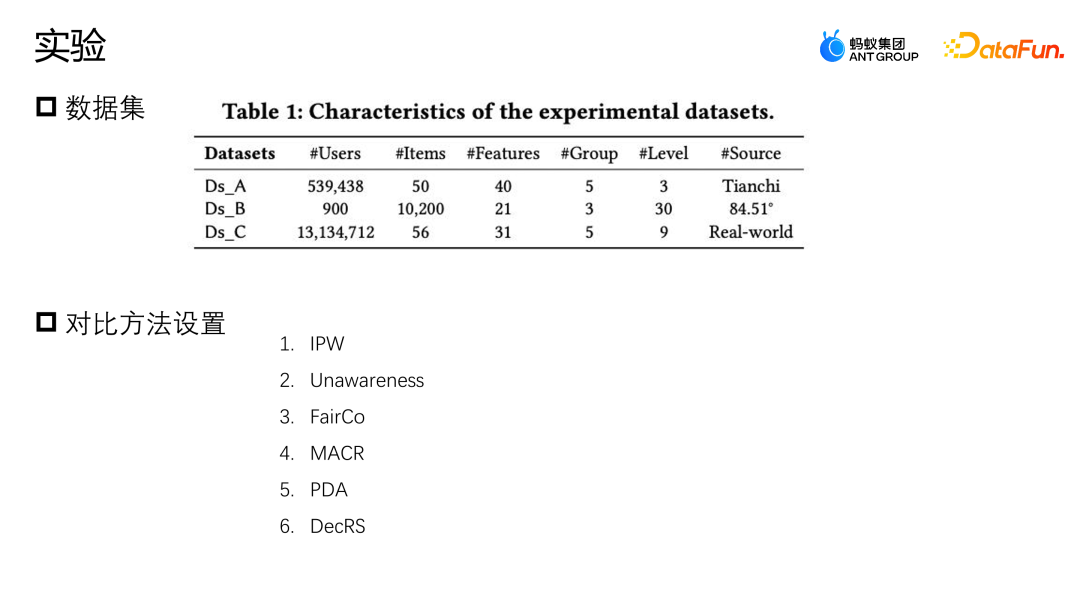
實驗採用了兩個開源的資料集，天池和 84.51（優惠券）資料集。透過採樣的方式模擬這種規則策略對整體資料的影響。同時，使用了某個真實的電商行銷活動場景所產生的數據，共同評測演算法的好壞。比較了一些主流的糾偏方法，例如IPW 是透過逆機率加權做糾偏；Unawareness 是透過去除偏差特徵來緩解偏差的影響；FairCo 是透過引入誤差項約束表徵來獲得相對無偏的估計；MACR 是透過多任務的框架分別估計使用者的一致性以及item 的流行程度，在預測階段減去一致性跟流行度這種方式來實現無偏估計；PDA 是透過因果乾預，對損失項做調整的方式去除流行性偏差的影響；DecRS 也是藉助後門調整去除資訊偏差，但是它只針對使用者視角的偏差進行修正。
實驗的評估指標是AUC，因為行銷推進場景對於推薦優惠券或推薦候選的商品只有一個，所以本質上是二分類的問題，因此採用AUC 來評估比較適合。比較了 DNN 和 MMOE 不同架構下的表現，可以看出，我們提出的 DMBR 模型相比於原始無糾偏方式以及其它糾偏方式都有著更好的效果。同時Ds_A 跟Ds_B 在模擬資料集上比真實的業務資料集上得到了更高的提升效果，這是因為真實業務資料集的資料會更複雜，不僅會受到規則策略的影響，還可能會受到其它因素的影響。
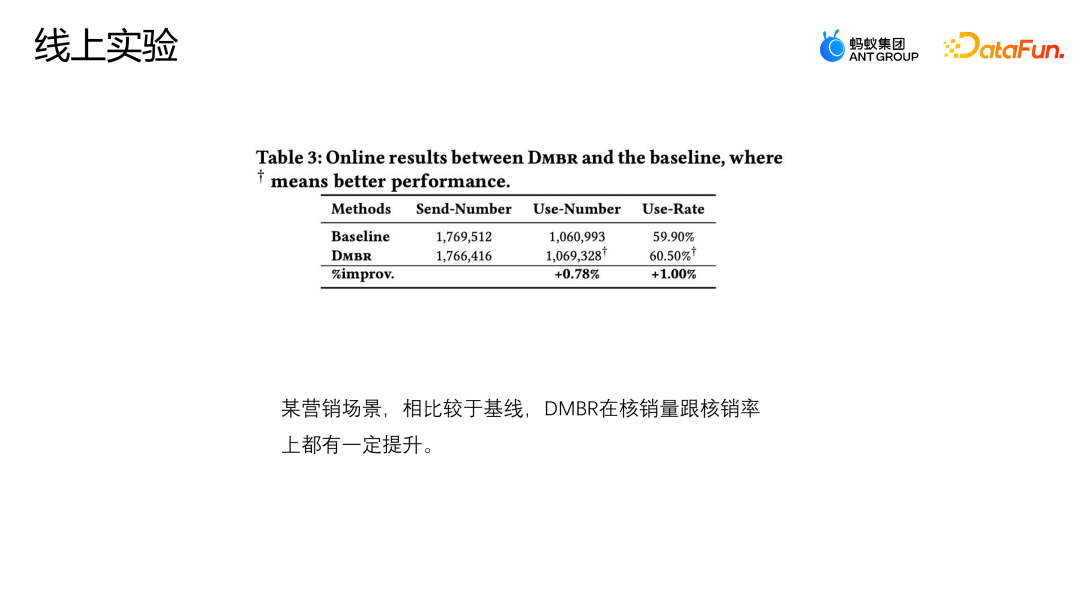
目前模型已在某電商行銷活動場景上線，上圖展示了線上的效果，對比基線模型，DMBR 模型在核銷率以及核子銷量上都有一定的提升。
因果糾偏的方法，在螞蟻主要應用在存在規則或存在策略約束的場景，例如廣告場景，可能會設定約束不同廣告的投放人群，一些針對寵物的廣告，會更多地投放給有寵物的使用者。電商行銷的場景，會設定一些策略來確保小商家的流量，避免所有流量都被大商家消耗。並確保用戶活動參與體驗，因為活動的整體預算有限，有一些薅羊毛的用戶反覆參與活動，就會佔用掉大量的資源，導致其他用戶的活動參與體驗較差。諸如此類的場景中，都有因果糾偏的應用。
以上是因果糾偏法在螞蟻行銷推薦場景中的應用的詳細內容。更多資訊請關注PHP中文網其他相關文章！
