軟硬約束下的軌跡產生:理論與程式碼詳解
本專案程式碼:
github.com/liangwq/robot_motion_planing
軌跡約束中的軟硬約束
前面的幾篇文章已經介紹了,軌跡約束的本質就是在做帶約束的軌跡擬合。輸入就是waypoint點list,約束條件有兩種硬約束和軟約束。所謂硬約束對應到數學形式就是代價函數,硬約束對應的就是最優化秋季的約束條件部分。對應到物理意義就是,為了獲得機器人可行走的安全的軌跡有:
- 把軌跡通過代價函數推離障礙物的方式
- 給出障礙物之間的可行走凸包走廊,透過硬約束讓機器人軌跡必須在凸包走廊行走

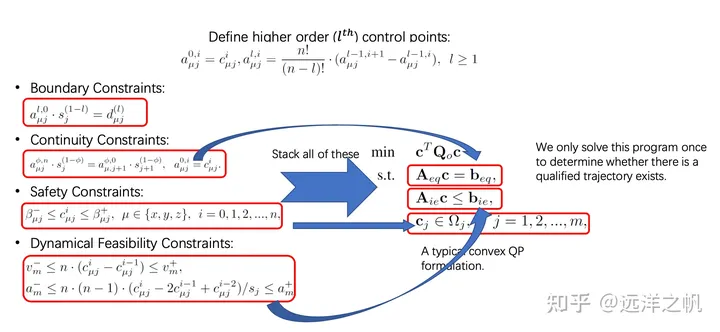
上圖展示的是軟硬約束下Bezier曲線擬合的求解的數學框架,以及如何把各種的限制條件轉成數學求解的代價函數(軟約束)或是求解的限制條件(軟約束)。 image.png
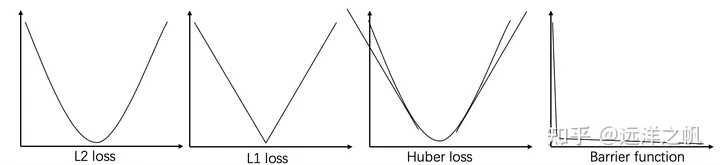
上面是對常用的代價函數約束的幾種表示方式的舉例。 image.png
Bezier曲線擬合軌跡
前面已經一篇文章介紹過貝賽爾曲線擬合的各種優點:
- 端點內插。貝塞爾曲線始終從第一個控制點開始,結束於最後一個控制點,並且不會經過任何其他控制點。
- 凸包。貝塞爾曲線 ( ) 由一組控制點 完全限制在由所有這些控制點定義的凸包內。
- 速度曲線。貝塞爾曲線 ( ) 的導數曲線 ′( ) 被稱為速度曲線,它也是一個由控制點定義的貝塞爾曲線,其中控制點為 ∙ ( 1− ),其中 是階數。
- 固定時間間隔。貝塞爾曲線始終在 [0,1] 上定義。
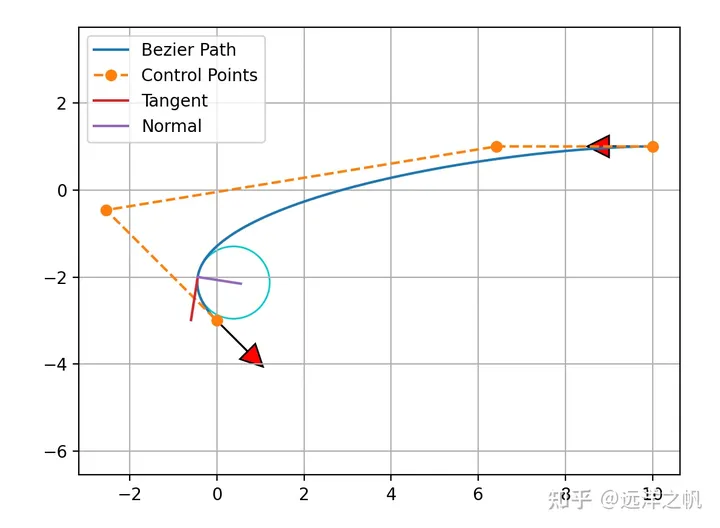
Fig1.一段軌跡用bezier曲線擬合image.png
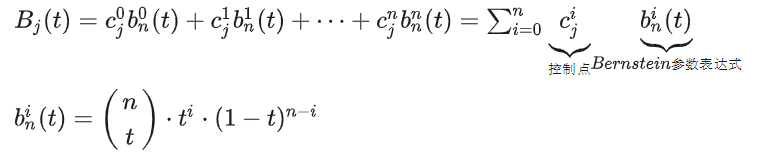
上面的兩個表達式對應的程式碼實作如下:
def bernstein_poly(n, i, t):"""Bernstein polynom.:param n: (int) polynom degree:param i: (int):param t: (float):return: (float)"""return scipy.special.comb(n, i) * t ** i * (1 - t) ** (n - i)def bezier(t, control_points):"""Return one point on the bezier curve.:param t: (float) number in [0, 1]:param control_points: (numpy array):return: (numpy array) Coordinates of the point"""n = len(control_points) - 1return np.sum([bernstein_poly(n, i, t) * control_points[i] for i in range(n + 1)], axis=0)
要用Bezier曲線來表示一段曲線,上面已經給了表達式和程式碼實現,現在缺的就是給定控制點,把控制點帶進來用Bezier曲線表達式來算出給定終點和結束點中需要畫的點座標。下列程式碼給了4個控制點、6個控制點的Bezier曲線實作;其中為了畫曲線需要算170個線上點。程式碼如下:
def calc_4points_bezier_path(sx, sy, syaw, ex, ey, eyaw, offset):"""Compute control points and path given start and end position.:param sx: (float) x-coordinate of the starting point:param sy: (float) y-coordinate of the starting point:param syaw: (float) yaw angle at start:param ex: (float) x-coordinate of the ending point:param ey: (float) y-coordinate of the ending point:param eyaw: (float) yaw angle at the end:param offset: (float):return: (numpy array, numpy array)"""dist = np.hypot(sx - ex, sy - ey) / offsetcontrol_points = np.array([[sx, sy], [sx + dist * np.cos(syaw), sy + dist * np.sin(syaw)], [ex - dist * np.cos(eyaw), ey - dist * np.sin(eyaw)], [ex, ey]])path = calc_bezier_path(control_points, n_points=170)return path, control_pointsdef calc_6points_bezier_path(sx, sy, syaw, ex, ey, eyaw, offset):"""Compute control points and path given start and end position.:param sx: (float) x-coordinate of the starting point:param sy: (float) y-coordinate of the starting point:param syaw: (float) yaw angle at start:param ex: (float) x-coordinate of the ending point:param ey: (float) y-coordinate of the ending point:param eyaw: (float) yaw angle at the end:param offset: (float):return: (numpy array, numpy array)"""dist = np.hypot(sx - ex, sy - ey) * offsetcontrol_points = np.array([[sx, sy], [sx + 0.25 * dist * np.cos(syaw), sy + 0.25 * dist * np.sin(syaw)], [sx + 0.40 * dist * np.cos(syaw), sy + 0.40 * dist * np.sin(syaw)], [ex - 0.40 * dist * np.cos(eyaw), ey - 0.40 * dist * np.sin(eyaw)], [ex - 0.25 * dist * np.cos(eyaw), ey - 0.25 * dist * np.sin(eyaw)], [ex, ey]])path = calc_bezier_path(control_points, n_points=170)return path, control_pointsdef calc_bezier_path(control_points, n_points=100):"""Compute bezier path (trajectory) given control points.:param control_points: (numpy array):param n_points: (int) number of points in the trajectory:return: (numpy array)"""traj = []for t in np.linspace(0, 1, n_points):traj.append(bezier(t, control_points))return np.array(traj)
有了一段Bezier曲線的擬合方式,接下來要做的就是如何產生多段Bezier曲線合成一條軌跡;並且是需要可以透過代價函數方式(軟約束) 必須經過指定點制定點銜接要連續(硬約束)來產生一條光滑的軌跡曲線。
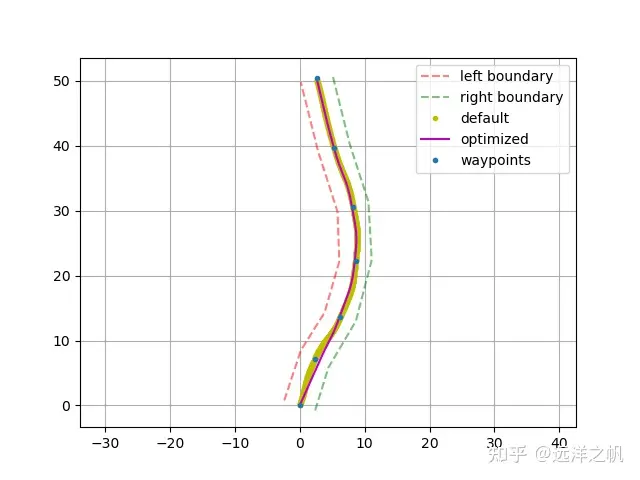
Fig2.無障礙物,帶bondary軌跡做了smooth優化Figure_1.png
多段Bezier曲線生成程式碼如下,其實原理很簡單,給定多個waypoint點,每相鄰兩個wayponit產生一段Bezizer曲線,程式碼如下:
# Bezier path one as per the approach suggested in# https://users.soe.ucsc.edu/~elkaim/Documents/camera_WCECS2008_IEEE_ICIAR_58.pdfdef cubic_bezier_path(self, ax, ay):dyaw, _ = self.calc_yaw_curvature(ax, ay)cx = []cy = []ayaw = dyaw.copy()for n in range(1, len(ax)-1):yaw = 0.5*(dyaw[n] + dyaw[n-1])ayaw[n] = yawlast_ax = ax[0]last_ay = ay[0]last_ayaw = ayaw[0]# for n waypoints, there are n-1 bezier curvesfor i in range(len(ax)-1):path, ctr_points = calc_4points_bezier_path(last_ax, last_ay, ayaw[i], ax[i+1], ay[i+1], ayaw[i+1], 2.0)cx = np.concatenate((cx, path.T[0][:-2]))cy = np.concatenate((cy, path.T[1][:-2]))cyaw, k = self.calc_yaw_curvature(cx, cy)last_ax = path.T[0][-1]last_ay = path.T[1][-1]return cx, cy
代價函數計算包含:曲率代價偏差代價距離代價連續性代價,同時還有邊界條件,軌跡必須在tube內的不等式約束,以及問題最佳化求解。具體程式碼實作如下:
# Objective function of cost to be minimizeddef cubic_objective_func(self, deviation):ax = self.waypoints.x.copy()ay = self.waypoints.y.copy()for n in range(0, len(deviation)):ax[n+1] -= deviation[n]*np.sin(self.waypoints.yaw[n+1])ay[n+1] += deviation[n]*np.cos(self.waypoints.yaw[n+1])bx, by = self.cubic_bezier_path(ax, ay)yaw, k = self.calc_yaw_curvature(bx, by)# cost of curvature continuityt = np.zeros((len(k)))dk = self.calc_d(t, k)absolute_dk = np.absolute(dk)continuity_cost = 10.0 * np.mean(absolute_dk)# curvature costabsolute_k = np.absolute(k)curvature_cost = 14.0 * np.mean(absolute_k)# cost of deviation from input waypointsabsolute_dev = np.absolute(deviation)deviation_cost = 1.0 * np.mean(absolute_dev)distance_cost = 0.5 * self.calc_path_dist(bx, by)return curvature_cost + deviation_cost + distance_cost + continuity_cost# Minimize objective function using scipy optimize minimizedef optimize_min_cubic(self):print("Attempting optimization minima")initial_guess = [0, 0, 0, 0, 0]bnds = ((-self.bound, self.bound), (-self.bound, self.bound), (-self.bound, self.bound), (-self.bound, self.bound), (-self.bound, self.bound))result = optimize.minimize(self.cubic_objective_func, initial_guess, bounds=bnds)ax = self.waypoints.x.copy()ay = self.waypoints.y.copy()if result.success:print("optimized true")deviation = result.xfor n in range(0, len(deviation)):ax[n+1] -= deviation[n]*np.sin(self.waypoints.yaw[n+1])ay[n+1] += deviation[n]*np.cos(self.waypoints.yaw[n+1])x, y = self.cubic_bezier_path(ax, ay)yaw, k = self.calc_yaw_curvature(x, y)self.optimized_path = Path(x, y, yaw, k)else:print("optimization failure, defaulting")exit()有障礙物的Bezier曲線軌跡生
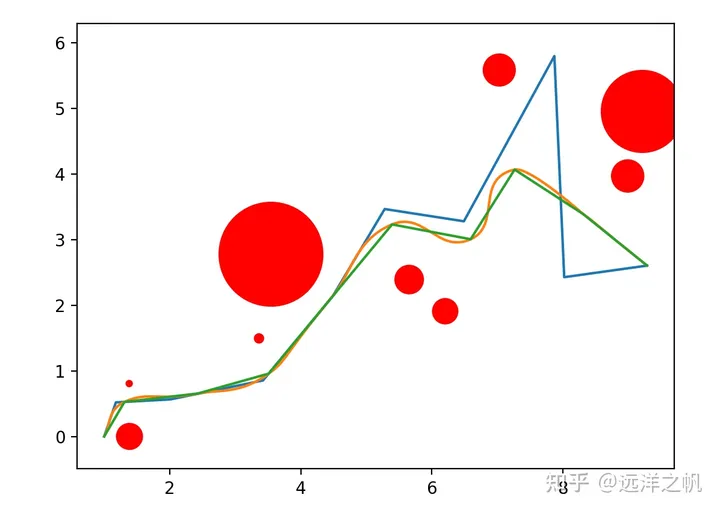
有障礙物的場景,透過代價函數讓生成的曲線遠離障礙物。從而得到一條可以安全行走的軌跡,以下是具體的程式碼實現。 optimizer_k中lambda函數f就是在求解軌跡在經過障礙物附近時候的代價,penalty1、penalty2就是在求曲線經過障礙物附近的具體代價值;
b.arc_len(granuality=10) B.arc_len(granuality =10) m_k penalty1 penalty2就是軌跡的整體代價。 for迴圈部分用scipy的optimize的minimize來求解軌跡。
def optimizer_k(cd, k, path, i, obs, curve_penalty_multiplier, curve_penalty_divider, curve_penalty_obst):"""Bezier curve optimizer that optimizes the curvature and path length by changing the distance of p1 and p2 from points p0 and p3, respectively. """p_tmp = copy.deepcopy(path)if i+3 > len(path)-1:b = CubicBezier()b.p0 = p_tmp[i]x, y = calc_p1(p_tmp[i], p_tmp[i + 1], p_tmp[i - 1], i, cd[0])b.p1 = Point(x, y)x, y = calc_p2(p_tmp[i-1], p_tmp[i + 0], p_tmp[i + 1], i, cd[1])b.p2 = Point(x, y)b.p3 = p_tmp[i + 1]B = CubicBezier()else:b = CubicBezier()b.p0 = p_tmp[i]x, y = calc_p1(p_tmp[i],p_tmp[i+1],p_tmp[i-1], i, cd[0])b.p1 = Point(x, y)x, y = calc_p2(p_tmp[i],p_tmp[i+1],p_tmp[i+2], i, cd[1])b.p2 = Point(x, y)b.p3 = p_tmp[i + 1]B = CubicBezier()B.p0 = p_tmp[i]x, y = calc_p1(p_tmp[i+1], p_tmp[i + 2], p_tmp[i], i, 10)B.p1 = Point(x, y)x, y = calc_p2(p_tmp[i+1], p_tmp[i + 2], p_tmp[i + 3], i, 10)B.p2 = Point(x, y)B.p3 = p_tmp[i + 1]m_k = b.max_k()if m_k>k:m_k= m_k*curve_penalty_multiplierelse:m_k = m_k/curve_penalty_dividerf = lambda x, y: max(math.sqrt((x[0] - y[0].x) ** 2 + (x[1] - y[0].y) ** 2) * curve_penalty_obst, 10) if math.sqrt((x[0] - y[0].x) ** 2 + (x[1] - y[0].y) ** 2) <h2 id="span-带飞行走廊的Bezier轨迹生成-span"><span>带飞行走廊的Bezier轨迹生成</span></h2><p>得益于贝赛尔曲线拟合的优势,如果我们可以让机器人可行走的轨迹转成多个有重叠区域的凸多面体,那么轨迹完全位于飞行走廊内。</p><p style="text-align:center;"><img src="/static/imghw/default1.png" data-src="https://img.php.cn/upload/article/000/887/227/170524425539093.png" class="lazy" alt="軟硬約束下的軌跡產生:理論與程式碼詳解"></p><p>image.png</p>
- 飞行走廊由凸多边形组成。
- 每个立方体对应于一段贝塞尔曲线。
- 此曲线的控制点被强制限制在多边形内部。
- 轨迹完全位于所有点的凸包内。
如何通过把障碍物地图生成可行凸包走廊
生成凸包走廊的方法目前有以下三大类的方法:
平行凸簇膨胀方法
从栅格地图出发,利用最小凸集生成算法,完成凸多面体的生成。其算法的思想是首先获得一个凸集,再沿着凸集的表面进行扩张,扩张之后再进行凸集检测,判断新扩张的集合是否保持为凸。一直扩张到不能再扩张为止,再提取凸集的边缘点,利用快速凸集生成算法,生成凸多面体。该算法的好处在于可以利用这种扩张的思路,将安全的多面体的体积尽可能的充满整个空间,因此获得的安全通道更大。但其也具有一定的缺点,就是计算量比较大,计算所需要的时间比较长,为了解决这个问题,在该文章中,又提出了采用GPU加速的方法,来加速计算。
基于凸分解的安全通道生成
基于凸分解的安全通道生成方法由四个步骤完成安全通道的生成,分别为:找到椭球、找到多面体、边界框、收缩。
半定规划的迭代区域膨胀
为了获取多面体,这个方法首先构造一个初始椭球,由一个以选定点为中心的单位球组成。然后,遍历障碍物,为每个障碍物生成一个超平面,该超平面与障碍物相切并将其与椭球分开。再次,这些超平面定义了一组线性约束,它们的交集是一个多面体。然后,可以在那个多面体中找到一个最大的椭球,使用这个椭球来定义一组新的分离超平面,从而定义一个新的多面体。选择生成分离超平面的方法,这样椭圆体的体积在迭代之间永远不会减少。可以重复这个过程,直到椭圆体的增长率低于某个阈值,此时我们返回多面体和内接椭圆体。这个方法具有迭代的思想,并且具有收敛判断的标准,算法的收敛快慢和初始椭球具有很大的关系。
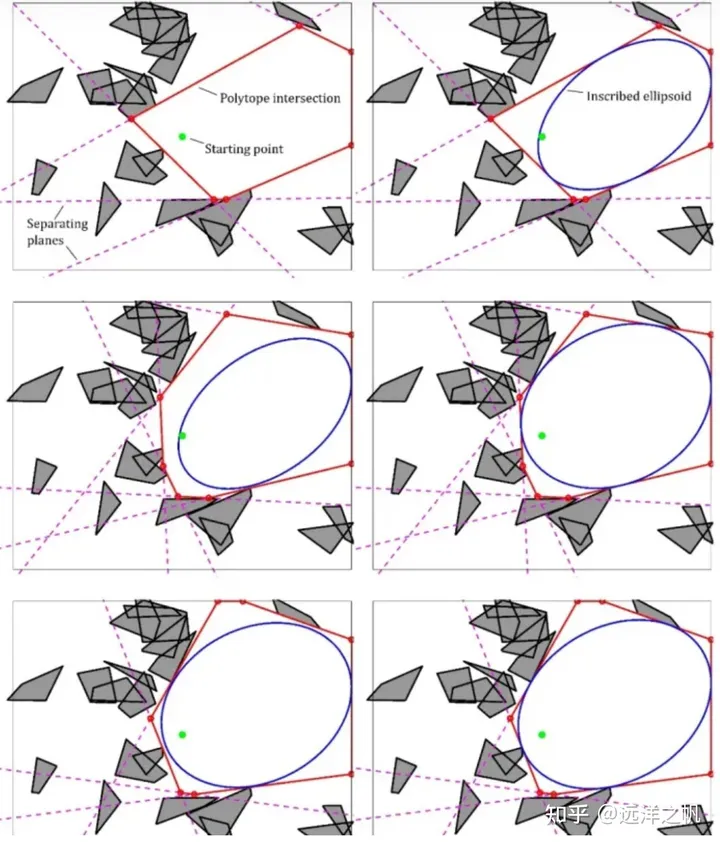
Fig3.半定规划的迭代区域膨胀。每一行即为一次迭代操作,直到椭圆体的增长率低于阈值。image.png
这篇文章介绍的是“半定规划的迭代区域膨胀”方法,具体代码实现如下:
# 根据输入路径对空间进行凸分解def decomp(self, line_points: list[np.array], obs_points: list[np.array], visualize=True):# 最终结果decomp_polygons = list()# 构建输入障碍物点的kdtreeobs_kdtree = KDTree(obs_points)# 进行空间分解for i in range(len(line_points) - 1):# 得到当前线段pf, pr = line_points[i], line_points[i + 1]print(pf)print(pr)# 构建初始多面体init_polygon = self.initPolygon(pf, pr)print(init_polygon.getInterPoints())print(init_polygon.getVerticals())# 过滤障碍物点candidate_obs_point_indexes = obs_kdtree.query_ball_point((pf + pr) / 2, np.linalg.norm([np.linalg.norm(pr - pf) / 2 + self.consider_range_, self.consider_range_]))local_obs_points = list()for index in candidate_obs_point_indexes:if init_polygon.inside(obs_points[index]):local_obs_points.append(obs_points[index])# 得到初始椭圆ellipse = self.findEllipse(pf, pr, local_obs_points)# 根据初始椭圆构建多面体polygon = self.findPolygon(ellipse, init_polygon, local_obs_points)# 进行保存decomp_polygons.append(polygon)if visualize:# 进行可视化plt.figure()# 绘制路径段plt.plot([pf[1], pr[1]], [pf[0], pr[0]], color="red")# 绘制初始多面体verticals = init_polygon.getVerticals()# 绘制多面体顶点plt.plot([v[1] for v in verticals] + [verticals[0][1]], [v[0] for v in verticals] + [verticals[0][0]], color="blue", linestyle="--")# 绘制障碍物点plt.scatter([p[1] for p in local_obs_points], [p[0] for p in local_obs_points], marker="o")# 绘制椭圆ellipse_x, ellipse_y = list(), list()for theta in np.linspace(-np.pi, np.pi, 1000):raw_point = np.array([np.cos(theta), np.sin(theta)])ellipse_point = np.dot(ellipse.C_, raw_point) + ellipse.d_ellipse_x.append(ellipse_point[0])ellipse_y.append(ellipse_point[1])plt.plot(ellipse_y, ellipse_x, color="orange")# 绘制最终多面体# 得到多面体顶点verticals = polygon.getVerticals()# 绘制多面体顶点plt.plot([v[1] for v in verticals] + [verticals[0][1]], [v[0] for v in verticals] + [verticals[0][0]], color="green")plt.show()return decomp_polygons# 构建初始多面体def initPolygon(self, pf: np.array, pr: np.array) -> Polygon:# 记录多面体的平面polygon_planes = list()# 得到线段方向向量dire = self.normalize(pr - pf)# 得到线段法向量dire_h = np.array([dire[1], -dire[0]])# 得到平行范围p_1 = pf + self.consider_range_ * dire_hp_2 = pf - self.consider_range_ * dire_hpolygon_planes.append(Hyperplane(dire_h, p_1))polygon_planes.append(Hyperplane(-dire_h, p_2))# 得到垂直范围p_3 = pr + self.consider_range_ * direp_4 = pf - self.consider_range_ * direpolygon_planes.append(Hyperplane(dire, p_3))polygon_planes.append(Hyperplane(-dire, p_4))# 构建多面体polygon = Polygon(polygon_planes)return polygon# 得到初始椭圆def findEllipse(self, pf: np.array, pr: np.array, obs_points: list[np.array]) -> Ellipse:# 计算长轴long_axis_value = np.linalg.norm(pr - pf) / 2axes = np.array([long_axis_value, long_axis_value])# 计算旋转rotation = self.vec2Rotation(pr - pf)# 计算初始椭圆C = np.dot(rotation, np.dot(np.array([[axes[0], 0], [0, axes[1]]]), np.transpose(rotation)))d = (pr + pf) / 2ellipse = Ellipse(C, d)# 得到椭圆内的障碍物点inside_obs_points = ellipse.insidePoints(obs_points)# 对椭圆进行调整,使得全部障碍物点都在椭圆外while inside_obs_points:# 得到与椭圆距离最近的点closest_obs_point = ellipse.closestPoint(inside_obs_points)# 将最近点转到椭圆坐标系下closest_obs_point = np.dot(np.transpose(rotation), closest_obs_point - ellipse.d_) # 根据最近点,在椭圆长轴不变的情况下对短轴进行改变,使得,障碍物点在椭圆上if Compare.small(closest_obs_point[0], axes[0]):axes[1] = np.abs(closest_obs_point[1]) / np.sqrt(1 - (closest_obs_point[0] / axes[0]) ** 2)# 更新椭圆ellipse.C_ = np.dot(rotation, np.dot(np.array([[axes[0], 0], [0, axes[1]]]), np.transpose(rotation)))# 更新椭圆内部障碍物inside_obs_points = ellipse.insidePoints(inside_obs_points, include_bound=False)return ellipse# 进行多面体的构建def findPolygon(self, ellipse: Ellipse, init_polygon: Polygon, obs_points: list[np.array]) -> Polygon:# 多面体由多个超平面构成polygon_planes = copy.deepcopy(init_polygon.hyper_planes_)# 初始化范围超平面remain_obs_points = obs_pointswhile remain_obs_points:# 得到与椭圆最近障碍物closest_point = ellipse.closestPoint(remain_obs_points)# 计算该处的切平面的法向量norm_vector = np.dot(np.linalg.inv(ellipse.C_), np.dot(np.linalg.inv(ellipse.C_), (closest_point - ellipse.d_)))norm_vector = self.normalize(norm_vector)# 构建平面hyper_plane = Hyperplane(norm_vector, closest_point)# 保存到多面体平面中polygon_planes.append(hyper_plane)# 去除切平面外部的障碍物new_remain_obs_points = list()for point in remain_obs_points:if Compare.small(hyper_plane.signDist(point), 0):new_remain_obs_points.append(point)remain_obs_points = new_remain_obs_pointspolygon = Polygon(polygon_planes)return polygon
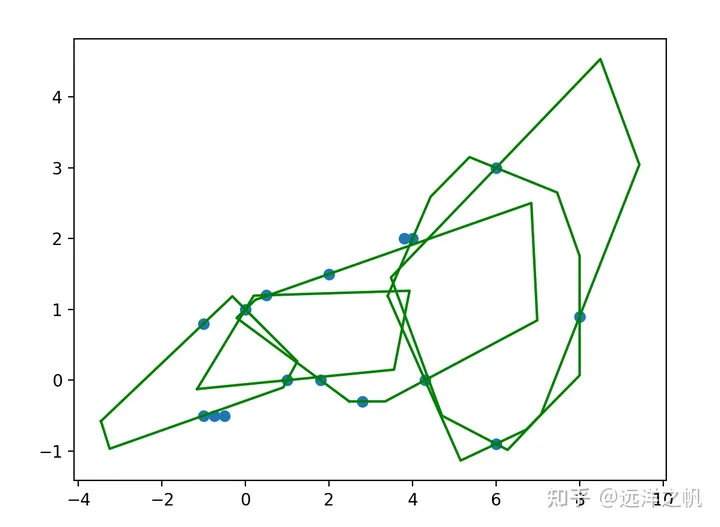
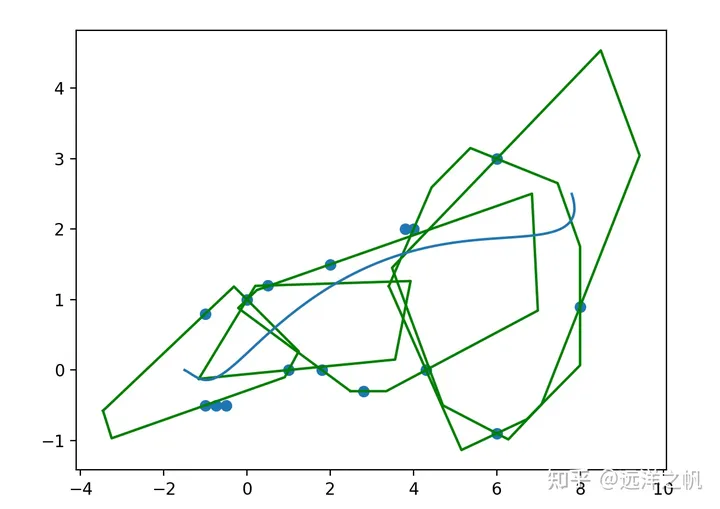
上面图是给定16个障碍物点,必经6个路径点后得到的凸包可行走廊,具体代码如下:
def main():# 路径点line_points = [np.array([-1.5, 0.0]), np.array([0.0, 0.8]), np.array([1.5, 0.3]), np.array([5, 0.6]), np.array([6, 1.2]), np.array([7.6, 2.2])]# 障碍物点obs_points = [np.array([4, 2.0]),np.array([6, 3.0]),np.array([2, 1.5]),np.array([0, 1]),np.array([1, 0]),np.array([1.8, 0]),np.array([3.8, 2]),np.array([0.5, 1.2]),np.array([4.3, 0]),np.array([8, 0.9]),np.array([2.8, -0.3]),np.array([6, -0.9]),np.array([-0.5, -0.5]),np.array([-0.75 ,-0.5]),np.array([-1, -0.5]),np.array([-1, 0.8])]convex_decomp = ConvexDecomp(2)decomp_polygons = convex_decomp.decomp(line_points, obs_points, False)#convex_decomp.decomp(line_points, obs_points,False)plt.figure()# 绘制障碍物点plt.scatter([p[0] for p in obs_points], [p[1] for p in obs_points], marker="o")# 绘制边界for polygon in decomp_polygons:verticals = polygon.getVerticals()# 绘制多面体顶点plt.plot([v[0] for v in verticals] + [verticals[0][0]], [v[1] for v in verticals] + [verticals[0][1]], color="green")#plt.plot(x_samples, y_samples)plt.show()
带凸包走廊求解
带凸包走廊的光滑轨迹生成。前面已经求解得到了可行的凸包走廊,这部分可以做为硬约束作为最优化求解的不等式条件。要求的光滑路径和必须经过点的点,这部分可以把必须经过点作为等式约束,光滑路径可以通过代价函数来实现。这样就可以把带软硬约束的轨迹生成框架各种技能点都用上了。
下面看具体代码实现:
# 进行优化def optimize(self, start_state: np.array, end_state: np.array, line_points: list[np.array], polygons: list[Polygon]):assert(len(line_points) == len(polygons) + 1)# 得到分段数量segment_num = len(polygons)assert(segment_num >= 1)# 计算初始时间分配time_allocations = list()for i in range(segment_num):time_allocations.append(np.linalg.norm(line_points[i+1] - line_points[i]) / self.vel_max_)# 进行优化迭代max_inter = 10cur_iter = 0while cur_iter <h2 id="span-小结-span"><span>小结:</span></h2><p>这篇文章介绍了带软硬约束的轨迹优化算法框架。第一部份介绍了软硬约束对应到最优求解问题数学上如何表示。第二部份介绍了贝赛尔曲线的代码实现,给出了具体的代码实现和讲解;并针对没有障碍物场景只给定waypoint点,生成光滑的Bezier轨迹的朴素求解代码实现。第三部份给出了带障碍物情况下如何做最优化求解,如何通过代价函数的方式来给轨迹施加推力让轨迹远离障碍物的代码实现。第四部分是一个综合性的例子,把软硬约束最优轨迹生成的求解框架做了一个综合呈现。详细的介绍了如何利用障碍物地图生成最大可行区域的凸包走廊,如何利用Bezier曲线的特性给定凸包两点生成路径一定在凸包中;以及如何利用代价行数来保证轨迹的光滑性、安全性,通过等式、不等式约束实现轨迹必须经过哪些点,某个点的运动状态如何。<br>这一系列的文章已经进入结尾的阶段,后面会简单介绍在碰到移动的物体时候单机器人如何处理;以及在多个机器人运行环境如何协同,最后会给出一个Motion Planning的综合实现例子讲解实际环境数据输入、前端规划、后端轨迹生成。至于定位和感知部分的内容后面可以根据情况而定是否在开一个新的系列来讲解介绍,对于更前沿的技术点会跟进论文做些文章分享。<br>最后本系列文章的代码在以下git链接,这部分代码相对零碎主要是配合文章理论来讲的,里面很多片段直接来源于网络整合。后面这可项目会持续维护,把项目代码(应该是c++实现,更体系)、整合进来,根据需要在看看有没必要整合出一个库。</p><p style="text-align:center;"><img src="/static/imghw/default1.png" data-src="https://img.php.cn/upload/article/000/887/227/170524425687764.jpg" class="lazy" alt="軟硬約束下的軌跡產生:理論與程式碼詳解"></p><p>原文链接:https://mp.weixin.qq.com/s/0EVgYKTxLzUj64L5jzMVug</p>
以上是軟硬約束下的軌跡產生:理論與程式碼詳解的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
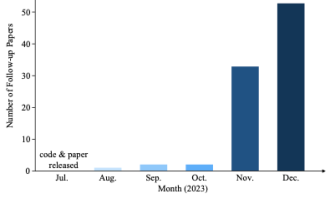 為何在自動駕駛方面Gaussian Splatting如此受歡迎,開始放棄NeRF?
Jan 17, 2024 pm 02:57 PM
為何在自動駕駛方面Gaussian Splatting如此受歡迎,開始放棄NeRF?
Jan 17, 2024 pm 02:57 PM
寫在前面&筆者的個人理解三維Gaussiansplatting(3DGS)是近年來在顯式輻射場和電腦圖形學領域出現的一種變革性技術。這種創新方法的特點是使用了數百萬個3D高斯,這與神經輻射場(NeRF)方法有很大的不同,後者主要使用隱式的基於座標的模型將空間座標映射到像素值。 3DGS憑藉其明確的場景表示和可微分的渲染演算法,不僅保證了即時渲染能力,而且引入了前所未有的控制和場景編輯水平。這將3DGS定位為下一代3D重建和表示的潛在遊戲規則改變者。為此我們首次系統性地概述了3DGS領域的最新發展與關
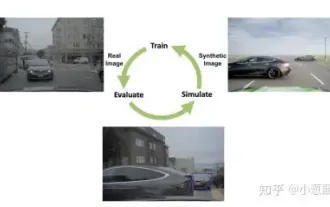 自動駕駛場景中的長尾問題怎麼解決?
Jun 02, 2024 pm 02:44 PM
自動駕駛場景中的長尾問題怎麼解決?
Jun 02, 2024 pm 02:44 PM
昨天面試被問到了是否做過長尾相關的問題,所以就想著簡單總結一下。自動駕駛長尾問題是指自動駕駛汽車中的邊緣情況,即發生機率較低的可能場景。感知的長尾問題是目前限制單車智慧自動駕駛車輛運行設計域的主要原因之一。自動駕駛的底層架構和大部分技術問題已經解決,剩下的5%的長尾問題,逐漸成了限制自動駕駛發展的關鍵。這些問題包括各種零碎的場景、極端的情況和無法預測的人類行為。自動駕駛中的邊緣場景"長尾"是指自動駕駛汽車(AV)中的邊緣情況,邊緣情況是發生機率較低的可能場景。這些罕見的事件
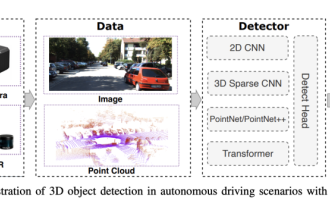 選擇相機還是光達?實現穩健的三維目標檢測的最新綜述
Jan 26, 2024 am 11:18 AM
選擇相機還是光達?實現穩健的三維目標檢測的最新綜述
Jan 26, 2024 am 11:18 AM
0.寫在前面&&個人理解自動駕駛系統依賴先進的感知、決策和控制技術,透過使用各種感測器(如相機、光達、雷達等)來感知周圍環境,並利用演算法和模型進行即時分析和決策。這使得車輛能夠識別道路標誌、檢測和追蹤其他車輛、預測行人行為等,從而安全地操作和適應複雜的交通環境。這項技術目前引起了廣泛的關注,並認為是未來交通領域的重要發展領域之一。但是,讓自動駕駛變得困難的是弄清楚如何讓汽車了解周圍發生的事情。這需要自動駕駛系統中的三維物體偵測演算法可以準確地感知和描述周圍環境中的物體,包括它們的位置、
 Stable Diffusion 3論文終於發布,架構細節大揭秘,對復現Sora有幫助?
Mar 06, 2024 pm 05:34 PM
Stable Diffusion 3論文終於發布,架構細節大揭秘,對復現Sora有幫助?
Mar 06, 2024 pm 05:34 PM
StableDiffusion3的论文终于来了!这个模型于两周前发布,采用了与Sora相同的DiT(DiffusionTransformer)架构,一经发布就引起了不小的轰动。与之前版本相比,StableDiffusion3生成的图质量有了显著提升,现在支持多主题提示,并且文字书写效果也得到了改善,不再出现乱码情况。StabilityAI指出,StableDiffusion3是一个系列模型,其参数量从800M到8B不等。这一参数范围意味着该模型可以在许多便携设备上直接运行,从而显著降低了使用AI
 SIMPL:用於自動駕駛的簡單高效的多智能體運動預測基準
Feb 20, 2024 am 11:48 AM
SIMPL:用於自動駕駛的簡單高效的多智能體運動預測基準
Feb 20, 2024 am 11:48 AM
原文標題:SIMPL:ASimpleandEfficientMulti-agentMotionPredictionBaselineforAutonomousDriving論文連結:https://arxiv.org/pdf/2402.02519.pdf程式碼連結:https://github.com/HKUST-Aerial-Robotics/SIMPLobotics單位論文想法:本文提出了一種用於自動駕駛車輛的簡單且有效率的運動預測基線(SIMPL)。與傳統的以代理為中心(agent-cent
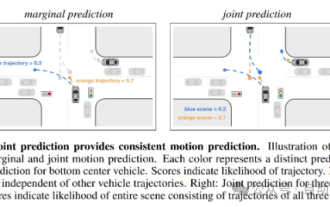 自動駕駛與軌跡預測看這篇就夠了!
Feb 28, 2024 pm 07:20 PM
自動駕駛與軌跡預測看這篇就夠了!
Feb 28, 2024 pm 07:20 PM
軌跡預測在自動駕駛中承擔著重要的角色,自動駕駛軌跡預測是指透過分析車輛行駛過程中的各種數據,預測車輛未來的行駛軌跡。作為自動駕駛的核心模組,軌跡預測的品質對於下游的規劃控制至關重要。軌跡預測任務技術堆疊豐富,需熟悉自動駕駛動/靜態感知、高精地圖、車道線、神經網路架構(CNN&GNN&Transformer)技能等,入門難度很高!許多粉絲期望能夠盡快上手軌跡預測,少踩坑,今天就為大家盤點下軌跡預測常見的一些問題和入門學習方法!入門相關知識1.預習的論文有沒有切入順序? A:先看survey,p
 聊聊端到端與下一代自動駕駛系統,以及端到端自動駕駛的一些迷思?
Apr 15, 2024 pm 04:13 PM
聊聊端到端與下一代自動駕駛系統,以及端到端自動駕駛的一些迷思?
Apr 15, 2024 pm 04:13 PM
最近一個月由於眾所周知的一些原因,非常密集地和業界的各種老師同學進行了交流。交流中必不可免的一個話題自然是端到端與火辣的特斯拉FSDV12。想藉此機會,整理當下這個時刻的一些想法和觀點,供大家參考和討論。如何定義端到端的自動駕駛系統,應該期望端到端解決什麼問題?依照最傳統的定義,端到端的系統指的是一套系統,輸入感測器的原始訊息,直接輸出任務關心的變數。例如,在影像辨識中,CNN相對於傳統的特徵提取器+分類器的方法就可以稱之為端到端。在自動駕駛任務中,輸入各種感測器的資料(相機/LiDAR
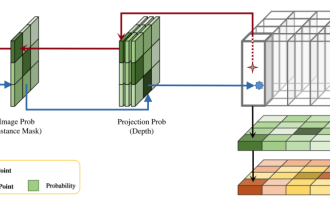 DualBEV:大幅超越BEVFormer、BEVDet4D,開卷!
Mar 21, 2024 pm 05:21 PM
DualBEV:大幅超越BEVFormer、BEVDet4D,開卷!
Mar 21, 2024 pm 05:21 PM
這篇論文探討了在自動駕駛中,從不同視角(如透視圖和鳥瞰圖)準確檢測物體的問題,特別是如何有效地從透視圖(PV)到鳥瞰圖(BEV)空間轉換特徵,這一轉換是透過視覺轉換(VT)模組實施的。現有的方法大致分為兩種策略:2D到3D和3D到2D轉換。 2D到3D的方法透過預測深度機率來提升密集的2D特徵,但深度預測的固有不確定性,尤其是在遠處區域,可能會引入不準確性。而3D到2D的方法通常使用3D查詢來採樣2D特徵,並透過Transformer學習3D和2D特徵之間對應關係的注意力權重,這增加了計算和部署的






