B樹刪除操作需要考慮節點所在位置和平衡,並且很有可能會發生下溢的情況。當一個節點包含的子節點數量少於它應該持有的最小數量時,就會發生下溢。
在不影響平衡情況下。
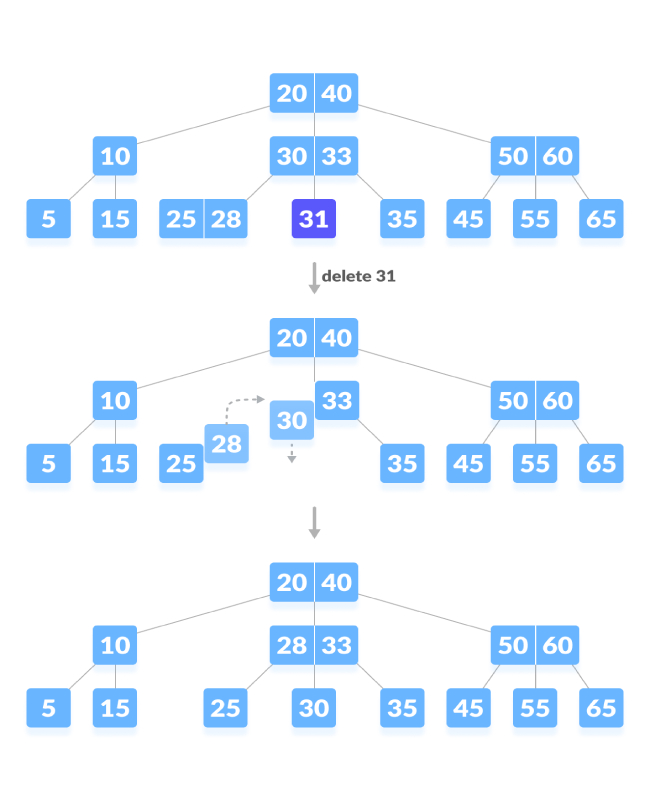
下溢情況。
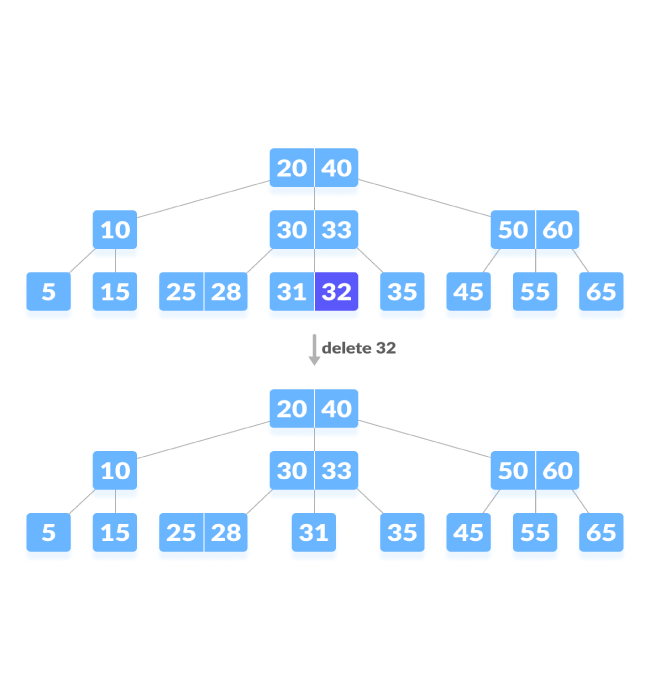
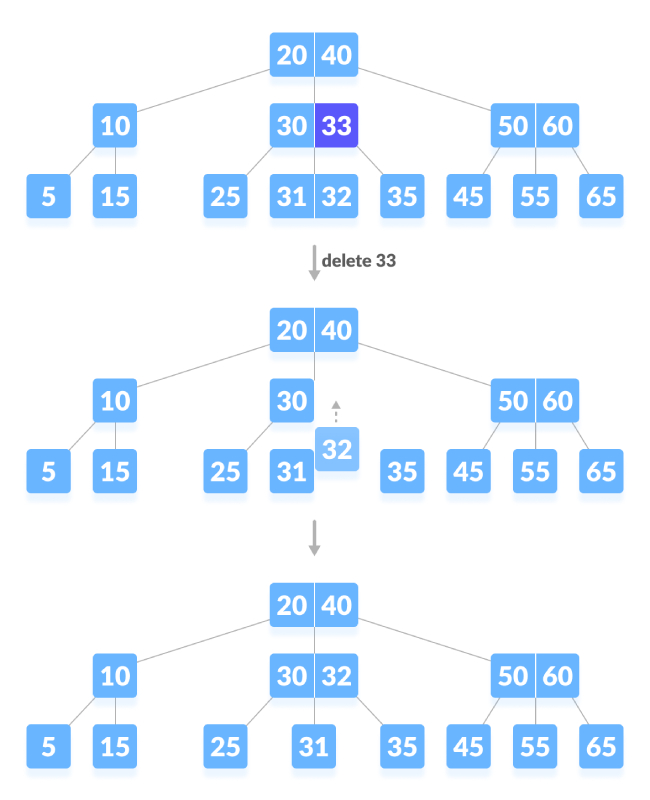
刪除內部節點。
# B树节点
class BTreeNode:
def __init__(self, leaf=False):
self.leaf = leaf
self.keys = []
self.child = []
class BTree:
def __init__(self, t):
self.root = BTreeNode(True)
self.t = t
# 插入元素
def insert(self, k):
root = self.root
if len(root.keys) == (2 * self.t) - 1:
temp = BTreeNode()
self.root = temp
temp.child.insert(0, root)
self.split_child(temp, 0)
self.insert_non_full(temp, k)
else:
self.insert_non_full(root, k)
def insert_non_full(self, x, k):
i = len(x.keys) - 1
if x.leaf:
x.keys.append((None, None))
while i >= 0 and k[0] < x.keys[i][0]:
x.keys[i + 1] = x.keys[i]
i -= 1
x.keys[i + 1] = k
else:
while i >= 0 and k[0] < x.keys[i][0]:
i -= 1
i += 1
if len(x.child[i].keys) == (2 * self.t) - 1:
self.split_child(x, i)
if k[0] > x.keys[i][0]:
i += 1
self.insert_non_full(x.child[i], k)
# 分开子节点
def split_child(self, x, i):
t = self.t
y = x.child[i]
z = BTreeNode(y.leaf)
x.child.insert(i + 1, z)
x.keys.insert(i, y.keys[t - 1])
z.keys = y.keys[t: (2 * t) - 1]
y.keys = y.keys[0: t - 1]
if not y.leaf:
z.child = y.child[t: 2 * t]
y.child = y.child[0: t - 1]
# 删除节点
def delete(self, x, k):
t = self.t
i = 0
while i < len(x.keys) and k[0] > x.keys[i][0]:
i += 1
if x.leaf:
if i < len(x.keys) and x.keys[i][0] == k[0]:
x.keys.pop(i)
return
return
if i < len(x.keys) and x.keys[i][0] == k[0]:
return self.delete_internal_node(x, k, i)
elif len(x.child[i].keys) >= t:
self.delete(x.child[i], k)
else:
if i != 0 and i + 2 < len(x.child):
if len(x.child[i - 1].keys) >= t:
self.delete_sibling(x, i, i - 1)
elif len(x.child[i + 1].keys) >= t:
self.delete_sibling(x, i, i + 1)
else:
self.delete_merge(x, i, i + 1)
elif i == 0:
if len(x.child[i + 1].keys) >= t:
self.delete_sibling(x, i, i + 1)
else:
self.delete_merge(x, i, i + 1)
elif i + 1 == len(x.child):
if len(x.child[i - 1].keys) >= t:
self.delete_sibling(x, i, i - 1)
else:
self.delete_merge(x, i, i - 1)
self.delete(x.child[i], k)
# 删除节点
def delete_internal_node(self, x, k, i):
t = self.t
if x.leaf:
if x.keys[i][0] == k[0]:
x.keys.pop(i)
return
return
if len(x.child[i].keys) >= t:
x.keys[i] = self.delete_predecessor(x.child[i])
return
elif len(x.child[i + 1].keys) >= t:
x.keys[i] = self.delete_successor(x.child[i + 1])
return
else:
self.delete_merge(x, i, i + 1)
self.delete_internal_node(x.child[i], k, self.t - 1)
# 删除前节点
def delete_predecessor(self, x):
if x.leaf:
return x.pop()
n = len(x.keys) - 1
if len(x.child[n].keys) >= self.t:
self.delete_sibling(x, n + 1, n)
else:
self.delete_merge(x, n, n + 1)
self.delete_predecessor(x.child[n])
# 删除继任节点
def delete_successor(self, x):
if x.leaf:
return x.keys.pop(0)
if len(x.child[1].keys) >= self.t:
self.delete_sibling(x, 0, 1)
else:
self.delete_merge(x, 0, 1)
self.delete_successor(x.child[0])
def delete_merge(self, x, i, j):
cnode = x.child[i]
if j > i:
rsnode = x.child[j]
cnode.keys.append(x.keys[i])
for k in range(len(rsnode.keys)):
cnode.keys.append(rsnode.keys[k])
if len(rsnode.child) > 0:
cnode.child.append(rsnode.child[k])
if len(rsnode.child) > 0:
cnode.child.append(rsnode.child.pop())
new = cnode
x.keys.pop(i)
x.child.pop(j)
else:
lsnode = x.child[j]
lsnode.keys.append(x.keys[j])
for i in range(len(cnode.keys)):
lsnode.keys.append(cnode.keys[i])
if len(lsnode.child) > 0:
lsnode.child.append(cnode.child[i])
if len(lsnode.child) > 0:
lsnode.child.append(cnode.child.pop())
new = lsnode
x.keys.pop(j)
x.child.pop(i)
if x == self.root and len(x.keys) == 0:
self.root = new
# 删除同一级的其他子节点
def delete_sibling(self, x, i, j):
cnode = x.child[i]
if i < j:
rsnode = x.child[j]
cnode.keys.append(x.keys[i])
x.keys[i] = rsnode.keys[0]
if len(rsnode.child) > 0:
cnode.child.append(rsnode.child[0])
rsnode.child.pop(0)
rsnode.keys.pop(0)
else:
lsnode = x.child[j]
cnode.keys.insert(0, x.keys[i - 1])
x.keys[i - 1] = lsnode.keys.pop()
if len(lsnode.child) > 0:
cnode.child.insert(0, lsnode.child.pop())
# 输出B树
def print_tree(self, x, l=0):
print("Level ", l, " ", len(x.keys), end=":")
for i in x.keys:
print(i, end=" ")
print()
l += 1
if len(x.child) > 0:
for i in x.child:
self.print_tree(i, l)
B = BTree(3)
for i in range(10):
B.insert((i, 2 * i))
B.print_tree(B.root)
B.delete(B.root, (8,))
print("\n")
B.print_tree(B.root)以上是詳解B樹刪除操作:使用Python實作B樹刪除操作的詳細圖解的詳細內容。更多資訊請關注PHP中文網其他相關文章!




