比較擴張卷積和空洞卷積的異同及相互關係

擴張卷積和空洞卷積是卷積神經網路中常用的操作,本文將詳細介紹它們的差異和關係。
一、擴張卷積
擴張卷積,又稱膨脹卷積或空洞卷積,是一種卷積神經網絡中的操作。它是在傳統的捲積操作基礎上進行的擴展,透過在卷積核中插入空洞來增大卷積核的感受野。這樣一來,網路可以更好地捕捉更大範圍的特徵。擴張卷積在影像處理領域有著廣泛的應用,能夠在不增加參數數量和運算量的情況下提升網路的效能。透過擴大卷積核的感受野,擴張卷積能夠更好地處理影像中的全局訊息,從而提高特徵提取的效果。
擴張卷積的主要思想是,在卷積核的周圍引入一些間隔,這些間隔允許卷積核以「跳躍」的方式在輸入特徵圖上移動,從而使輸出特徵圖的尺寸增大,同時保持卷積核的大小不變。具體來說,假設輸入特徵圖為X,卷積核為K,輸出特徵圖為Y,則擴張卷積可以表示為:
##Y_{i,j}= \sum_{m}\sum_{n}X_{(i m\times r),(j n\times r)}K_{m,n} 其中r為擴張率,表示卷積核中空洞的大小,m和n是卷積核中的行和列索引。透過改變擴張率r的大小,可以得到不同感受野的特徵圖。 二、空洞卷積 空洞卷積是一種在卷積神經網路中常用的捲積操作,它與擴張卷積的概念非常相似,但是它們在實現上略有不同。空洞卷積與傳統的捲積操作不同的地方在於,在卷積操作中插入了一些空洞,這些空洞可以使卷積核在輸入特徵圖上「跳躍式」地移動,從而使得輸出特徵圖的尺寸增大,同時保持卷積核的大小不變。 空洞卷積的主要想法是,在卷積核中插入一些空洞,這些空洞可以使卷積核在輸入特徵圖上「跳躍式」地移動,從而使得輸出特徵圖的尺寸增加,同時保持卷積核的大小不變。具體來講,假設輸入特徵圖為X,卷積核為K,輸出特徵圖為Y,則空洞卷積可以表示為: Y_{i,j}= \sum_{m}\sum_{n}X_{(i m\times r),(j n\times r)}K_{m,n} 其中r是空洞率,表示插入空洞的大小,m和n是卷積核中的行和列索引。透過改變空洞率r的大小,可以得到不同感受野的特徵圖。 三、擴張卷積和空洞卷積的關係 #擴張卷積和空洞卷積的概念非常相似,它們都是在傳統的捲積操作基礎上進行的擴展。事實上,擴張卷積可以看作是空洞卷積的一種特殊形式,因為擴張卷積中的空洞率d其實就是空洞卷積中的空洞率r-1。因此,擴張卷積可以看作是一種特殊的空洞卷積,它是透過插入空洞來擴大卷積核的感受野,並且在實現上也可以使用空洞卷積的方式來實現。 另外,擴張卷積和空洞卷積都可以用於卷積神經網路中的多種任務,如影像分類、語義分割等,它們在不同的任務中都能夠提高卷積神經網路的效能。但是,由於擴張卷積中的空洞率d是離散的,因此它的感受野相對於空洞卷積來說要略微不夠精確。因此,在需要提高感受野的任務中,空洞卷積可能會更常用。 總之,擴張卷積和空洞卷積都是卷積神經網路中常用的捲積操作,它們可以相互轉化,也可以在不同的任務中使用,具體使用哪種卷積操作需要根據特定的任務需求來決定。以上是比較擴張卷積和空洞卷積的異同及相互關係的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 探究RNN、LSTM和GRU的概念、區別和優劣
Jan 22, 2024 pm 07:51 PM
探究RNN、LSTM和GRU的概念、區別和優劣
Jan 22, 2024 pm 07:51 PM
在時間序列資料中,觀察值之間存在依賴關係,因此它們不是相互獨立的。然而,傳統的神經網路將每個觀察視為獨立的,這限制了模型對時間序列資料的建模能力。為了解決這個問題,循環神經網路(RNN)被引入,它引入了記憶的概念,透過在網路中建立資料點之間的依賴關係來捕捉時間序列資料的動態特性。透過循環連接,RNN可以將先前的資訊傳遞到當前觀察中,從而更好地預測未來的值。這使得RNN成為處理時間序列資料任務的強大工具。但是RNN是如何實現這種記憶的呢? RNN透過神經網路中的回饋迴路實現記憶,這是RNN與傳統神經
 利用雙向LSTM模型進行文本分類的案例
Jan 24, 2024 am 10:36 AM
利用雙向LSTM模型進行文本分類的案例
Jan 24, 2024 am 10:36 AM
雙向LSTM模型是一種用於文字分類的神經網路。以下是一個簡單範例,示範如何使用雙向LSTM進行文字分類任務。首先,我們需要匯入所需的函式庫和模組:importosimportnumpyasnpfromkeras.preprocessing.textimportTokenizerfromkeras.preprocessing.sequenceimportpad_sequencesfromkeras.modelsimportSequentialfromkeras.layersimportDense,Emquencesfromkeras.modelsimportSequentialfromkeras.layersimportDense,Emquencesfromkeras.modelsimportSequentialfromkeras.layers
 計算神經網路的浮點操作數(FLOPS)
Jan 22, 2024 pm 07:21 PM
計算神經網路的浮點操作數(FLOPS)
Jan 22, 2024 pm 07:21 PM
FLOPS是電腦效能評估的標準之一,用來衡量每秒鐘的浮點運算次數。在神經網路中,FLOPS常用於評估模型的計算複雜度和計算資源的使用率。它是一個重要的指標,用來衡量電腦的運算能力和效率。神經網路是一種複雜的模型,由多層神經元組成,用於進行資料分類、迴歸和聚類等任務。訓練和推斷神經網路需要進行大量的矩陣乘法、卷積等計算操作,因此計算複雜度非常高。 FLOPS(FloatingPointOperationsperSecond)可以用來衡量神經網路的運算複雜度,進而評估模型的運算資源使用效率。 FLOP
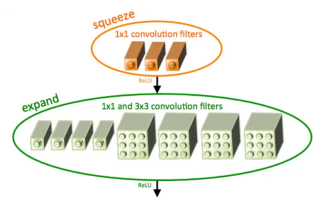 SqueezeNet簡介及其特點
Jan 22, 2024 pm 07:15 PM
SqueezeNet簡介及其特點
Jan 22, 2024 pm 07:15 PM
SqueezeNet是一種小巧而精確的演算法,它在高精度和低複雜度之間達到了很好的平衡,因此非常適合資源有限的移動和嵌入式系統。 2016年,DeepScale、加州大學柏克萊分校和史丹佛大學的研究人員提出了一個緊湊高效的捲積神經網路(CNN)-SqueezeNet。近年來,研究人員對SqueezeNet進行了多次改進,其中包括SqueezeNetv1.1和SqueezeNetv2.0。這兩個版本的改進不僅提高了準確性,還降低了計算成本。 SqueezeNetv1.1在ImageNet資料集上的精確度
 比較擴張卷積和空洞卷積的異同及相互關係
Jan 22, 2024 pm 10:27 PM
比較擴張卷積和空洞卷積的異同及相互關係
Jan 22, 2024 pm 10:27 PM
擴張卷積和空洞卷積是卷積神經網路常用的操作,本文將詳細介紹它們的差異和關係。一、擴張卷積擴張卷積,又稱為膨脹卷積或空洞卷積,是一種卷積神經網路中的操作。它是在傳統的捲積操作基礎上進行的擴展,透過在卷積核中插入空洞來增大卷積核的感受野。這樣一來,網路可以更好地捕捉更大範圍的特徵。擴張卷積在影像處理領域有著廣泛的應用,能夠在不增加參數數量和運算量的情況下提升網路的效能。透過擴大卷積核的感受野,擴張卷積能夠更好地處理影像中的全局訊息,從而提高特徵提取的效果。擴張卷積的主要想法是,在卷積核的周圍引入一些
 孿生神經網路:原理與應用解析
Jan 24, 2024 pm 04:18 PM
孿生神經網路:原理與應用解析
Jan 24, 2024 pm 04:18 PM
孿生神經網路(SiameseNeuralNetwork)是一種獨特的人工神經網路結構。它由兩個相同的神經網路組成,這兩個網路共享相同的參數和權重。同時,這兩個網路也共享相同的輸入資料。這個設計靈感源自於孿生兄弟,因為這兩個神經網路在結構上完全相同。孿生神經網路的原理是透過比較兩個輸入資料之間的相似度或距離來完成特定任務,如影像匹配、文字匹配和人臉辨識。在訓練過程中,網路會試圖將相似的資料映射到相鄰的區域,將不相似的資料映射到遠離的區域。這樣,網路能夠學習如何對不同的資料進行分類或匹配,以實現相應
 使用卷積神經網路進行影像降噪
Jan 23, 2024 pm 11:48 PM
使用卷積神經網路進行影像降噪
Jan 23, 2024 pm 11:48 PM
卷積神經網路在影像去噪任務中表現出色。它利用學習到的濾波器對雜訊進行過濾,從而恢復原始影像。本文詳細介紹了基於卷積神經網路的影像去噪方法。一、卷積神經網路概述卷積神經網路是一種深度學習演算法,透過多個卷積層、池化層和全連接層的組合來進行影像特徵學習和分類。在卷積層中,透過卷積操作提取影像的局部特徵,從而捕捉影像中的空間相關性。池化層則透過降低特徵維度來減少計算量,並保留主要特徵。全連接層負責將學習到的特徵與標籤進行映射,以實現影像的分類或其他任務。這種網路結構的設計使得卷積神經網路在影像處理與識
 因果卷積神經網絡
Jan 24, 2024 pm 12:42 PM
因果卷積神經網絡
Jan 24, 2024 pm 12:42 PM
因果卷積神經網路是一種針對時間序列資料中的因果關係問題而設計的特殊卷積神經網路。相較於常規卷積神經網絡,因果卷積神經網絡在保留時間序列的因果關係方面具有獨特的優勢,並在時間序列資料的預測和分析中廣泛應用。因果卷積神經網路的核心思想是在卷積操作中引入因果關係。傳統的捲積神經網路可以同時感知到當前時間點前後的數據,但在時間序列預測中,這可能導致資訊外洩問題。因為當前時間點的預測結果會受到未來時間點的資料影響。因果卷積神經網路解決了這個問題,它只能感知到當前時間點以及先前的數據,無法感知到未來的數






