理解機器學習中的ReLU函數

什麼是ReLU函數？

ReLU函數是定義為f(x)=max(0,x)的數學函數，其中x是任意實數。簡單來說，如果x小於或等於0，則函數傳回0。否則返回x。

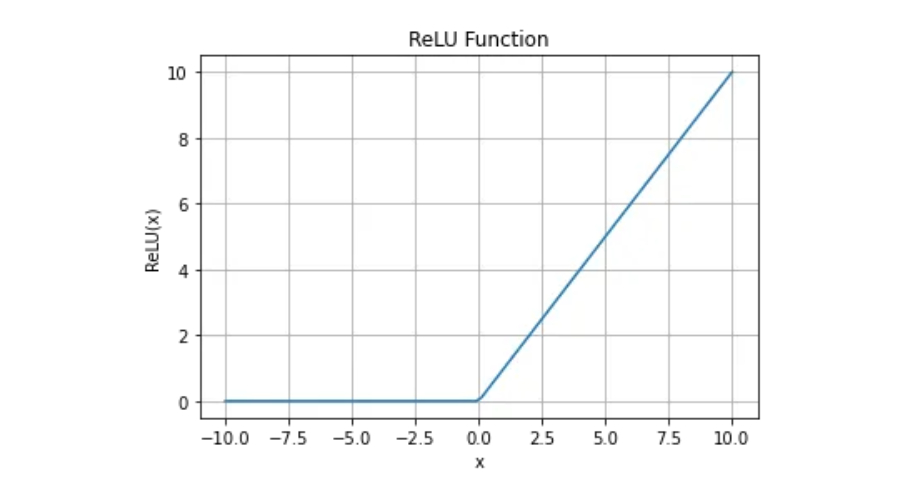
ReLU函數的連續性與可微性

對於可微分的函數，它必須先是連續的。 ReLU函數滿足連續性要求，但在x=0的導數不存在，因此ReLU函數在該點不可微。

那麼為什麼深度學習中仍然會使用ReLU函數呢？

雖然ReLU函數在x=0處不可微，但我們仍可以透過微調最佳化演算法來在深度學習中應用它。梯度下降是一種最佳化演算法，用於最小化成本函數。當ReLU函數在x=0處沒有定義導數時，我們可以將其設定為0或其他任意值，並繼續進行最佳化過程。這樣我們可以利用ReLU函數的非線性特性來提升深度學習模型的表現。

總的來說，ReLU激活函數是深度學習網路中最受歡迎的激活函數之一。它的簡單和高計算效率使其成為訓練過程中收斂性提高的重要工具。儘管在x=0處不可微，但這並不影響它在梯度下降中的應用。因此，ReLU函數是機器學習領域中多功能且強大的工具。

ReLU函數的優點

1.計算簡單。

整流器函數實作起來很簡單，需要一個max()函數。

2.代表性稀疏性

稀疏表示是表示學習中的理想屬性，因為它有助於加速學習和簡化模型。它使得神經網路的隱藏層激活可以包含一個或多個真零值，這意味著負輸入也可以輸出真零值。這種能力使得神經網路能夠更好地處理大規模數據，並且可以減少計算和儲存資源的需求。因此，稀疏表示對於優化神經網路的效能和效率非常重要。

3.線性行為

整流器函數與線性激活函數外觀和行為相似。適用於線性或接近線性行為的最佳化。

以上是理解機器學習中的ReLU函數的詳細內容。更多資訊請關注PHP中文網其他相關文章！