深入解析線性判別分析LDA

線性判別分析(Linear Discriminant Analysis,LDA)是一種經典的模式分類方法,可用於降維和特徵提取。在人臉辨識中,LDA常用於特徵提取。其主要想法是將資料投影到低維度子空間,以實現不同類別資料在該子空間中的最大差異性,同一類別資料在該子空間中的最小變異數。透過計算類間散佈矩陣和類內散佈矩陣的特徵向量,可以獲得最佳投影方向,從而實現資料的降維和特徵提取。 LDA在實際應用上具有較好的分類效能與運算效率,被廣泛應用於影像辨識、模式辨識等領域。
線性判別分析(LDA)的基本概念是透過將高維度資料投影到低維空間,使得不同類別的資料在該空間中的分佈能夠得到最大的差異性。它透過將原始資料投影到一個新的空間中,使得同一類別的資料盡可能地靠近,而不同類別之間的資料盡可能地遠離,從而提高分類的準確率。具體而言,LDA透過計算類內散度矩陣和類間散度矩陣之間的比值來確定投影方向,使得投影後的資料盡可能地滿足這一目標。這樣一來,在投影後的低維空間中,同一類別的資料會更加緊密地聚集在一起,不同類別之間的資料則會更加分散,從而方便進行分類。
線性判別分析LDA的基本原理
線性判別分析(LDA)是一種常見的監督學習演算法,主要用於降維和分類。其基本原理如下:
假設我們有一組帶有標籤的資料集,每個樣本都有多個特徵向量。我們的目標是將這些數據點分類到不同的標籤中。為了實現這一目標,我們可以進行以下步驟: 1. 計算每個標籤下所有樣本特徵向量的平均向量,得到每個標籤的平均向量。 2. 計算所有資料點的總平均值向量,該向量是整個資料集中所有樣本特徵向量的平均值。 3. 計算每個標籤的類內散度矩陣。類內散度矩陣是每個標籤內所有樣本特徵向量與該標籤的平均值向量之差的乘積,然後將每個標籤的結果加起來。 4. 計算類內散度矩陣的逆矩陣與類間散度矩陣的乘積,得到投影向量。 5. 將投影向量進行歸一化,以確保其長度為1。 6. 將資料點投影到投影向量上,得到一維特徵向量。 7. 利用設定的閾值將一維特徵向量分類到不同的標籤。 透過上述步驟,我們可以將多維的資料點投影到一維的特徵空間中,並根據閾值將其分類到對應的標籤中。這種方法可以幫助我們實現資料的降維和分類。
LDA的核心思想是計算平均值向量和散度矩陣,以發現資料內部結構和類別關係。透過投影向量將資料降維,並利用分類器進行分類任務。
線性判別分析LDA計算過程
LDA的計算過程可以概括為以下步驟:
計算每個類別的平均值向量,即每個類別內所有樣本的特徵向量平均值,並計算總平均值向量。
計算類內散度矩陣時,需將每個類別內樣本的特徵向量與平均向量之差乘累積加。
計算類間散度矩陣是透過每個類別內總平均值向量與每個類別平均值向量之差的乘積,再將所有類別的結果累加。
4.計算投影向量,即將特徵向量投影到一維空間上的向量,該向量是類內散度矩陣的逆矩陣與類間散度矩陣的乘積,再將此向量歸一化。
5.對所有樣本進行投影,得到一維特徵向量。
6.根據一維特徵向量對樣本進行分類。
7.評估分類效能。
線性判別分析LDA方法優缺點
線性判別分析LDA是常見的監督學習演算法,其優點和缺點如下:
優點:
- LDA是一種線性分類方法,簡單易懂,易於實現。
- LDA不僅可以用於分類,還可以用於降維,可以提高分類器的效能,減少運算量。
- LDA假設資料滿足常態分佈,對雜訊有一定的穩健性,對於雜訊較小的數據,LDA的分類效果很好。
- LDA考慮了資料的內部結構和類別之間的關係,能夠盡可能地保留資料的判別訊息,提高了分類的準確性。
缺點:
- LDA assumes that the covariance matrices of each category are equal, but in practical applications, it is difficult to meet this assumption and may affect the classification effect.
- LDA has poor classification effect for non-linearly separable data.
- LDA is sensitive to outliers and noise, which may affect the classification effect.
- LDA needs to calculate the inverse matrix of the covariance matrix. If the feature dimension is too high, it may cause a very large amount of calculation and is not suitable for processing high-dimensional data.
In summary, linear discriminant analysis LDA is suitable for processing low-dimensional, linearly separable and data that satisfies the normal distribution, but it is not suitable for high-dimensional, non-linear separable or data that does not satisfy the normal distribution. For situations such as state distribution, other algorithms need to be selected.
以上是深入解析線性判別分析LDA的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 位元組跳動剪映推出 SVIP 超級會員:連續包年 499 元,提供多種 AI 功能
Jun 28, 2024 am 03:51 AM
位元組跳動剪映推出 SVIP 超級會員:連續包年 499 元,提供多種 AI 功能
Jun 28, 2024 am 03:51 AM
本站6月27日訊息,剪映是由位元組跳動旗下臉萌科技開發的一款影片剪輯軟體,依託於抖音平台且基本面向該平台用戶製作短影片內容,並相容於iOS、安卓、Windows 、MacOS等作業系統。剪映官方宣布會員體系升級,推出全新SVIP,包含多種AI黑科技,例如智慧翻譯、智慧劃重點、智慧包裝、數位人合成等。價格方面,剪映SVIP月費79元,年費599元(本站註:折合每月49.9元),連續包月則為59元每月,連續包年為499元每年(折合每月41.6元) 。此外,剪映官方也表示,為提升用戶體驗,向已訂閱了原版VIP
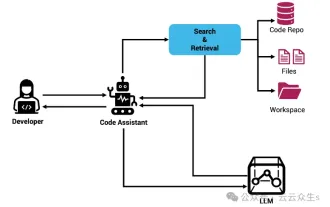 使用Rag和Sem-Rag提供上下文增強AI編碼助手
Jun 10, 2024 am 11:08 AM
使用Rag和Sem-Rag提供上下文增強AI編碼助手
Jun 10, 2024 am 11:08 AM
透過將檢索增強生成和語意記憶納入AI編碼助手,提升開發人員的生產力、效率和準確性。譯自EnhancingAICodingAssistantswithContextUsingRAGandSEM-RAG,作者JanakiramMSV。雖然基本AI程式設計助理自然有幫助,但由於依賴對軟體語言和編寫軟體最常見模式的整體理解,因此常常無法提供最相關和正確的程式碼建議。這些編碼助手產生的代碼適合解決他們負責解決的問題,但通常不符合各個團隊的編碼標準、慣例和風格。這通常會導致需要修改或完善其建議,以便將程式碼接受到應
 七個很酷的GenAI & LLM技術性面試問題
Jun 07, 2024 am 10:06 AM
七個很酷的GenAI & LLM技術性面試問題
Jun 07, 2024 am 10:06 AM
想了解更多AIGC的內容,請造訪:51CTOAI.x社群https://www.51cto.com/aigc/譯者|晶顏審校|重樓不同於網路上隨處可見的傳統問題庫,這些問題需要跳脫常規思維。大語言模型(LLM)在數據科學、生成式人工智慧(GenAI)和人工智慧領域越來越重要。這些複雜的演算法提升了人類的技能,並在許多產業中推動了效率和創新性的提升,成為企業保持競爭力的關鍵。 LLM的應用範圍非常廣泛,它可以用於自然語言處理、文字生成、語音辨識和推薦系統等領域。透過學習大量的數據,LLM能夠產生文本
 微調真的能讓LLM學到新東西嗎:引入新知識可能讓模型產生更多的幻覺
Jun 11, 2024 pm 03:57 PM
微調真的能讓LLM學到新東西嗎:引入新知識可能讓模型產生更多的幻覺
Jun 11, 2024 pm 03:57 PM
大型語言模型(LLM)是在龐大的文字資料庫上訓練的,在那裡它們獲得了大量的實際知識。這些知識嵌入到它們的參數中,然後可以在需要時使用。這些模型的知識在訓練結束時被「具體化」。在預訓練結束時,模型實際上停止學習。對模型進行對齊或進行指令調優,讓模型學習如何充分利用這些知識,以及如何更自然地回應使用者的問題。但是有時模型知識是不夠的,儘管模型可以透過RAG存取外部內容,但透過微調使用模型適應新的領域被認為是有益的。這種微調是使用人工標註者或其他llm創建的輸入進行的,模型會遇到額外的實際知識並將其整合
 你所不知道的機器學習五大學派
Jun 05, 2024 pm 08:51 PM
你所不知道的機器學習五大學派
Jun 05, 2024 pm 08:51 PM
機器學習是人工智慧的重要分支,它賦予電腦從數據中學習的能力,並能夠在無需明確編程的情況下改進自身能力。機器學習在各個領域都有廣泛的應用,從影像辨識和自然語言處理到推薦系統和詐欺偵測,它正在改變我們的生活方式。機器學習領域存在著多種不同的方法和理論,其中最具影響力的五種方法被稱為「機器學習五大派」。這五大派分別為符號派、聯結派、進化派、貝葉斯派和類推學派。 1.符號學派符號學(Symbolism),又稱符號主義,強調利用符號進行邏輯推理和表達知識。該學派認為學習是一種逆向演繹的過程,透過現有的
 為大模型提供全新科學複雜問答基準與評估體系,UNSW、阿貢、芝加哥大學等多家機構共同推出SciQAG框架
Jul 25, 2024 am 06:42 AM
為大模型提供全新科學複雜問答基準與評估體系,UNSW、阿貢、芝加哥大學等多家機構共同推出SciQAG框架
Jul 25, 2024 am 06:42 AM
編輯|ScienceAI問答(QA)資料集在推動自然語言處理(NLP)研究中發揮著至關重要的作用。高品質QA資料集不僅可以用於微調模型,也可以有效評估大語言模型(LLM)的能力,尤其是針對科學知識的理解和推理能力。儘管目前已有許多科學QA數據集,涵蓋了醫學、化學、生物等領域,但這些數據集仍有一些不足之處。其一,資料形式較為單一,大多數為多項選擇題(multiple-choicequestions),它們易於進行評估,但限制了模型的答案選擇範圍,無法充分測試模型的科學問題解答能力。相比之下,開放式問答
 SK 海力士 8 月 6 日將展示 AI 相關新品:12 層 HBM3E、321-high NAND 等
Aug 01, 2024 pm 09:40 PM
SK 海力士 8 月 6 日將展示 AI 相關新品:12 層 HBM3E、321-high NAND 等
Aug 01, 2024 pm 09:40 PM
本站8月1日消息,SK海力士今天(8月1日)發布博文,宣布將出席8月6日至8日,在美國加州聖克拉拉舉行的全球半導體記憶體峰會FMS2024,展示諸多新一代產品。未來記憶體和儲存高峰會(FutureMemoryandStorage)簡介前身是主要面向NAND供應商的快閃記憶體高峰會(FlashMemorySummit),在人工智慧技術日益受到關注的背景下,今年重新命名為未來記憶體和儲存高峰會(FutureMemoryandStorage),以邀請DRAM和儲存供應商等更多參與者。新產品SK海力士去年在
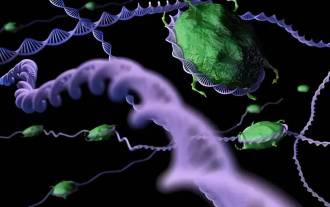 SOTA性能,廈大多模態蛋白質-配體親和力預測AI方法,首次結合分子表面訊息
Jul 17, 2024 pm 06:37 PM
SOTA性能,廈大多模態蛋白質-配體親和力預測AI方法,首次結合分子表面訊息
Jul 17, 2024 pm 06:37 PM
編輯|KX在藥物研發領域,準確有效地預測蛋白質與配體的結合親和力對於藥物篩選和優化至關重要。然而,目前的研究並沒有考慮到分子表面訊息在蛋白質-配體相互作用中的重要作用。基於此,來自廈門大學的研究人員提出了一種新穎的多模態特徵提取(MFE)框架,該框架首次結合了蛋白質表面、3D結構和序列的信息,並使用交叉注意機制進行不同模態之間的特徵對齊。實驗結果表明,該方法在預測蛋白質-配體結合親和力方面取得了最先進的性能。此外,消融研究證明了該框架內蛋白質表面資訊和多模態特徵對齊的有效性和必要性。相關研究以「S






