
動測量,這些資料主要分為時序資料和事件資料兩大類。時序資料指的是實值-時間序列(通常有固定的時間間隔),例如CPU使用率等;而事件資料指的是記錄了特定事件發生的序列,例如記憶體溢位事件等。 為了確保產品的服務品質、減少服務宕機時間,從而避免更大的經濟損失,對關鍵的服務事件的診斷顯得尤為重要。在實際的維運工作中,對服務事件進行診斷時,維運人員可以透過分析與服務事件相關的時序數據,來分析事件發生的原因。雖然這個相關關係不能完全準確的反映真實的因果關係,但仍然可以為診斷提供一些很好的線索和啟示。
那麼問題來了,如何自動的判斷事件和時序資料的關聯關係呢?
問題 在本文中,作者將事件(E)和時序(S)資料相關關係問題轉換為兩樣本問題(two-sample problem),並使用鄰近演算法(nearest neighbor method)判斷是否相關。主要回答了三個問題:A. E和S之間是否有相關關係? B.若有相關關係,E和S的時間先後順序是什麼? E先發生,還是S先發生? C. E和S的單調關係。假設S(或E)先發生,S的增加還是降低導致的E發生? 如圖,事件為程式A和B的運行,時序資料為CPU使用率。可以發現,事件(程式A的運作)與時序資料(CPU使用率)有相關關係,且是程式A運作後CPU使用率發生升高的變化。
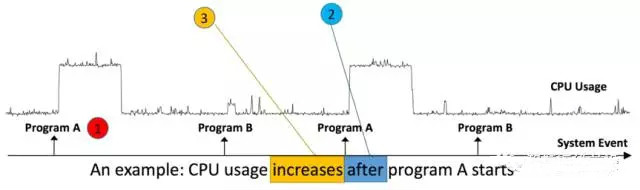
文章的演算法架構主要分為三部分,分別解決相關性、時間先後順序、單調性三個問題。接下來將對這三個部分進行詳細介紹。
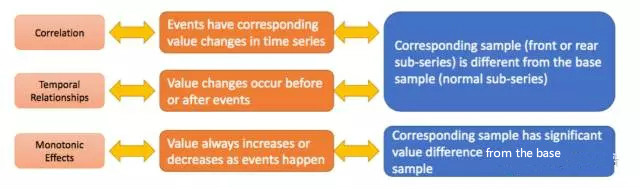
文章將相關性的判斷轉換為兩個樣本問題,兩個樣本假設檢定的核心是判斷兩個樣本是否來自相同的分佈。先選取事件發生前(或後)對應的N段長為k的時序樣本數據,以A1表示。樣本組A2則是在時間序列上隨機選取一系列長度為k的樣本資料。樣本集為A1並上A2。如果E和S相關,則A1和A2的分佈不同,否則分佈相同。怎樣來判斷A1和A2的分佈是否相同?我們看下面這個例子:
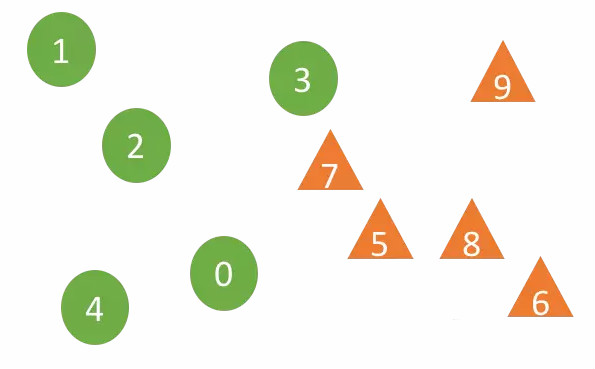
#上圖中樣本0-4來自樣本組A1,5-9屬於樣本組A2,使用DTW演算法來計算兩個樣本之間的距離(DTW演算法可以很好的適應序列資料的伸縮和位移)。某個屬於樣本組Ai(i=1或2)的樣本X,對於X的r個最近鄰居樣本,與X屬於相同樣本組的個數越多則意味著樣本組A1和A2分佈更不同,即E和S越相關。例如,取鄰居個數r=2,樣本7的兩個最近鄰居分別是來自兩個不同樣本組的3和5,但是樣本5的兩個最近鄰居是來自相同樣本組A2的7和8。 文章使用信賴係數(Confident coefficient)來判斷「假設檢定H1」(兩個分佈不相同,即E和S相關)的可信度,置信係數越大,H1越可信。演算法的兩個關鍵參數:最近鄰居個數r和時間序列長度k,鄰居個數為樣本個數的自然對數,時序資料的自相關函數曲線的第一個峰值為序列長度。
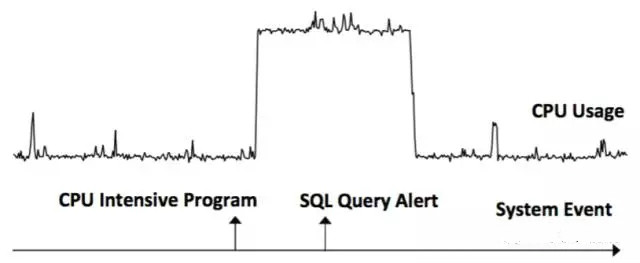
#選取事件發生前後的序列與隨機選取的時間序列求相關性,結果為Dr和Df。 若Dr為True,Df為False,代表E的發生先於S的發生(E -> S)。若Dr為False,Df為True,或Dr為True,Df為True,代表S的發生先於E的發生(S -> E)。如下圖例子,事件CPU Intensive Program –> 時序資料CPU Usage,時序資料CPU Usage -> 事件SQL Query Alert。
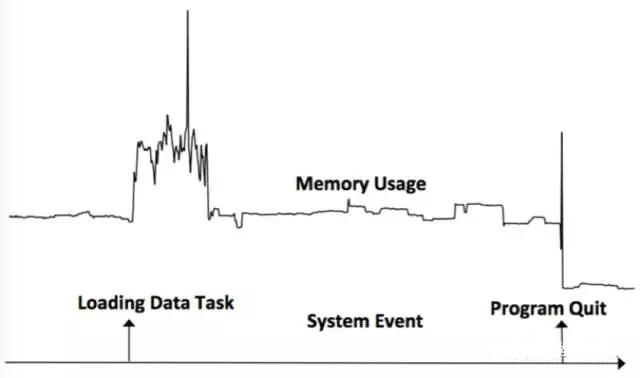
#單調性由事件發生前後時間序列的變化來判斷,如果事件發生後的時間序列比之前的序列取值要大,單調性為增加,否則為降低。 如下圖所示事件loading Data Task導致了Memory Usage的增加,事件Program Quit導致了Memory Usage的降低。
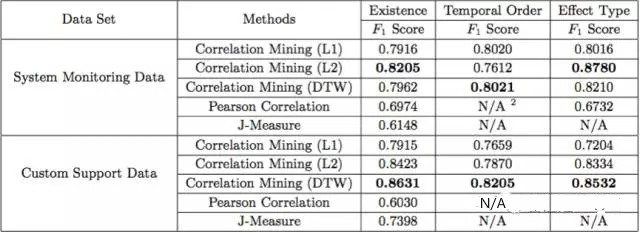
文章透過使用微軟的系統監控資料和客服團隊的資料對演算法效能進行驗證,資料分別是24個S(記憶體、CPU和DISK資料)和52個E (特定任務的執行),7 個S (HTTP狀態碼)和57個E (服務主題),評價標準為F-score。結果顯示DTW距離比其他的距離(L1和L2)整體表現更好,演算法整體比兩個baseline演算法(皮爾森相關和J-Measure)表現好。
文章介紹了一套全新的無監督的方法研究事件和時序資料的關係,回答了三個問題:E和S是否相關? E和S發生的先後順序?以及單調關係是什麼?相比較現在很多的相關關係研究,主要是事件之間的關聯關係和時序資料之間的關聯關係,本文則著重事件和時序資料間的關係,是第一個回答了事件和時序資料間上述三個問題的工作。
事件診斷一直是維運領域一個很重要的工作,事件和時序資料的相關性不僅可以為事件診斷提供很好的啟發,而且在幫助進行根因分析等都能提供很好的線索。作者在微軟的內部資料集上對演算法做了驗證,並且取得了很好的效果,這對於學術和工業屆都有很高的價值。
以上是微軟AIOps工作的種種細節揭秘的詳細內容。更多資訊請關注PHP中文網其他相關文章!




