清華姚班本科生連發兩作,十年來最大改進:矩陣乘法接近理論最優
透過消除「隱藏的低效」問題,電腦科學家提出了一種比以往更快的大型矩陣相乘新方法。
矩陣乘法作為眾多GPU算子的基礎操作,在高效能運算中扮演重要角色,也是AI等應用的關鍵組成部分。雖然其演算法本身相對簡單,但為了實現更高的速度,人們多年來一直在不斷努力優化。然而,優化的程度一直受到一定限制。
在最新一期的《量子雜誌》報導中,我們發現了兩篇能夠加快矩陣乘法速度的論文。在這兩篇論文的撰寫中,清華大學姚班一位大四本科生積極參與,為該領域的演算法改進帶來了嶄新的前景。
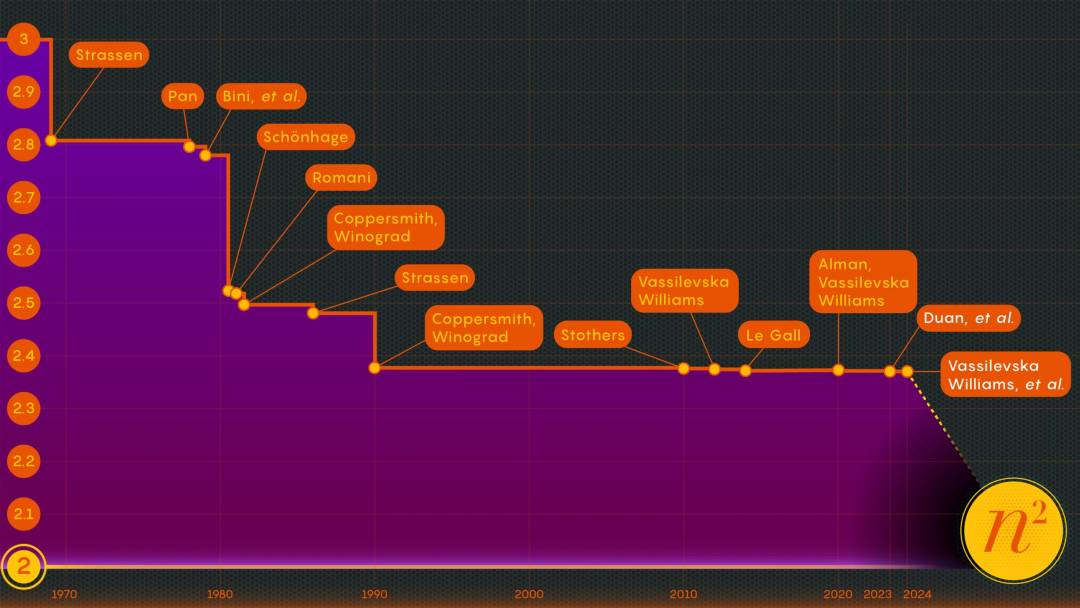
矩陣乘法改進出現新「奇點」
電腦科學家是一群非常嚴格要求的人。他們追求的不僅是解決問題,更在於以最高效的方式達成目標。
以矩陣或數字數組相乘為例,1812年,法國數學家Jacques Philippe Marie Binet提出了一套基本規則,至今仍在教導學生。這套規則被廣泛應用,但近年來一些數學家發現了簡化和加速過程的方法。

法國數學家中 Jacques Philippe Marie Binet。
目前,加速矩陣乘法過程已經成為數學和電腦科學的交叉領域。研究人員一直在努力改進這個過程,儘管近幾十年來的進展有限。名古屋大學的電腦科學家François Le Gall指出,自1987年以來,對矩陣乘法的數值改進一直進展緩慢且難以實現。他認為在當前情況下,進一步提升矩陣乘法效率面臨巨大挑戰,需要更多的創新和突破。儘管困難重重,科學家們仍在不懈地努力尋求突破,希望能夠找到新的方法和技術,以提高矩陣乘法的計算速度和效率。這表明矩陣乘法優化仍然是一個具有挑戰性的課題,需要集合
清華大學的段然(Ran Duan)、週任飛(Renfei Zhou)和加州大學伯克利分校的Hongxun Wu 近期在解決這個長期在存在的問題上取得了重要進展,他們的研究成果在一篇87 頁的論文中得以詳細展示。 Le Gall 對這三位研究者的工作給予了高度評價,他認為儘管改進相對較小,但在概念上卻是前所未有的重大突破。
這篇論文被電腦科學領域的頂會 FOCS 2023 接收。

論文 v1 發佈於 2022 年 10 月,v5 在 2023 年 11 月。論文地址:https://arxiv.org/abs/2210.10173
其中,段然為清華大學交叉資訊研究所副教授,主要研究方向為圖論演算法、資料結構、計算理論。 Hongxun Wu 為加州大學柏克萊分校二年級博士生,也是清華姚班出身。
週任飛為清華姚班 2020 級的大四本科生,主修理論計算機科學(TCS)。他主要研究(簡潔)資料結構和快速矩陣乘法,並對 TCS 的其他領域具有廣泛興趣,例如串流演算法、博弈論和線上演算法等。
此前,週任飛曾在理論計算機科學頂級會議 FOCS/SODA 上發表多篇論文。

三位研究者的論文揭示了以前未知且未開發的潛在改進來源,並且已經取得了成果。 2024 年 1 月發表的第二篇論文(週任飛同樣參與撰寫)以此為基礎,展示如何進一步增強矩陣乘法。

論文地址:https://epubs.siam.org/doi/10.1137/1.9781611977912.134
哈佛大學理論計算機科學家William Kuszmaul 對此表示,這是一項重大的技術突破,也是十多年來我們所看到的矩陣乘法的最大改進。
矩陣乘法要改進什麼問題
矩陣乘法可能看起來是一個晦澀的問題,但它是一種基本的計算運算。它被融入了人們每天使用的大部分演算法中,用於各種任務,從顯示更清晰的電腦圖形到解決網路理論中的物流問題。就像在計算的其他領域一樣,速度至關重要。即使是微小的改進最終也可能大大減少所需的時間、計算能力和金錢。但目前,理論家主要感興趣的是弄清楚這個過程到底能夠有多快。
傳統的兩個n×n 矩陣相乘的方法—— 即將第一個矩陣中每一行的數字與第二個矩陣中每一列的數字相乘—— 需要進行n³ 次獨立的乘法操作。對於 2 乘 2 的矩陣而言,這意味著需要進行 2³,也就是 8 次乘法運算。
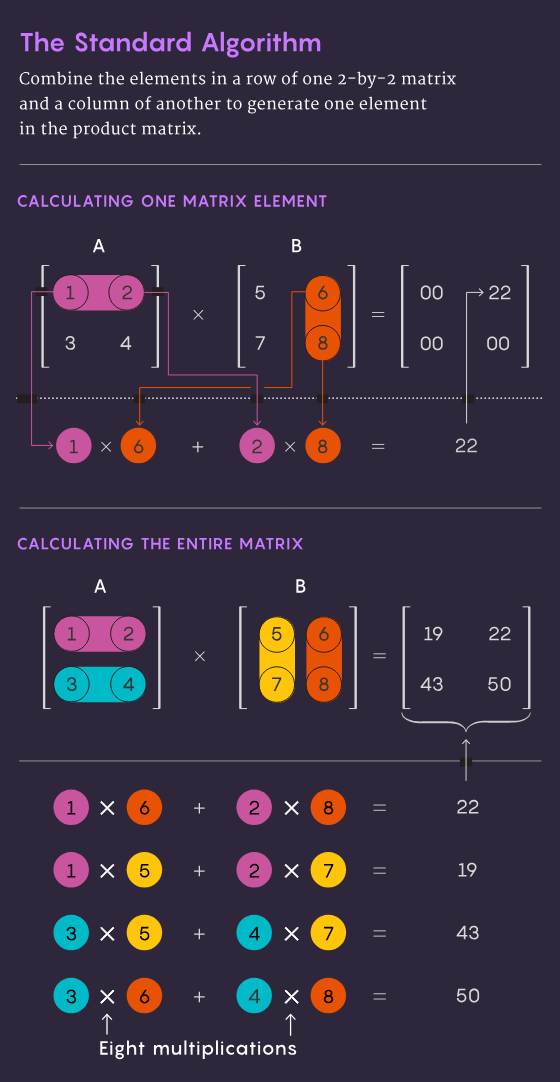
1969 年,數學家Volker Strassen 發現了一個更精巧的方法,只需7 個乘法步驟和18 個加法步驟,就能完成2×2 矩陣的乘法運算。兩年後,電腦科學家 Shmuel Winograd 證明,對於 2×2 矩陣來說,7 步乘法確實是絕對最小值。
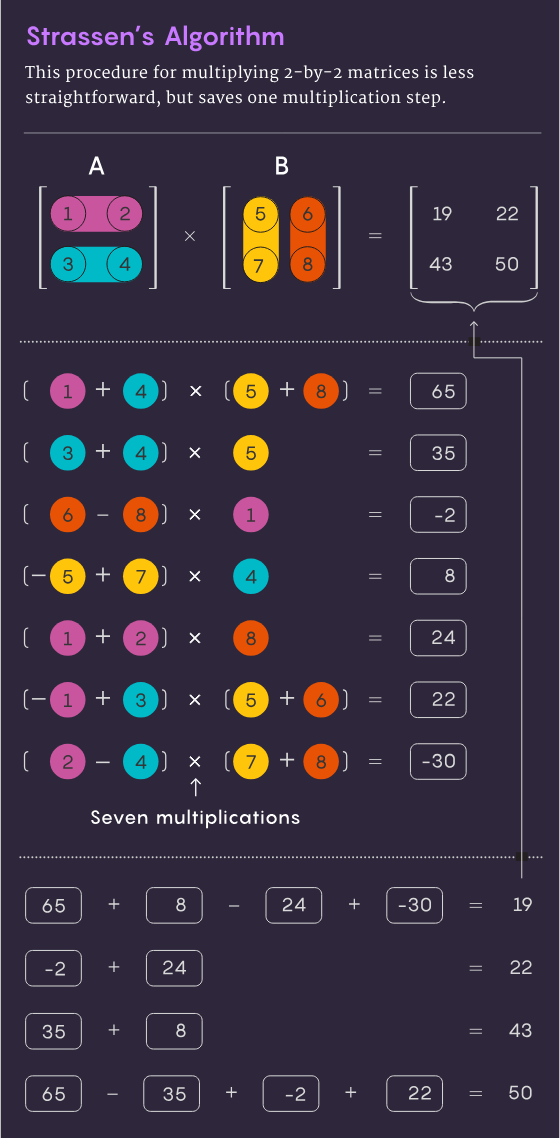
Strassen 利用同樣的想法證明,所有較大的 n×n 矩陣也可以用少於 n3 步驟的方法進行乘法運算。這個策略中的一個關鍵因素涉及一個稱為分解的程序:將一個大矩陣分解成一個個更小的子矩陣,這些子矩陣最終可能小到 2×2 甚至 1×1(只是單個數字)。
對於將巨型陣列分解成小塊的理由相當簡單,麻省理工學院的電腦科學家Virginia Vassilevska Williams 說:「對於一個大矩陣(例如100×100 的矩陣),人類很難想到最佳的演算法。」即使是3 乘3 的矩陣也還沒完全解決。 「然而,人們可以使用已經為小矩陣開發的快速演算法來獲得更大矩陣的快速演算法。」
研究人員確定,速度的關鍵在於減少乘法步驟的數量,盡可能將指數從n3 (傳統方法)降低。可能的最低值 n² 基本上就是寫出答案所需的時間。計算機科學家稱這個指數為 Ω,即 ω。 nω 是當 n 越來越大時,成功將兩個 n×n 矩陣相乘所需的最少步驟。同為2024 年1 月論文合著者的周任飛說:「這項工作的重點,是看你能接近2 多少,並且是否可以在理論上實現。」
雷射法
1986 年,Strassen 取得了另一個重大突破,他推出了矩陣乘法的雷射法。 Strassen 用它決定了 ω 的上限值為 2.48。雖然該方法只是大型矩陣乘法的一個步驟,但卻是最重要的步驟之一,因為研究人員一直在不斷改進它。
一年後,Winograd 和 Don Coppersmith 推出了一種新演算法,對雷射法進行了完美的補充。這套工具的組合在後來幾乎所有加速矩陣乘法的研究中都被應用了。
以下是一個簡化的方法,讓我們來看看這些不同的元素是如何結合在一起的。讓我們從兩個大型矩陣 A 和 B 開始,將它們相乘。首先,你要把它們分解成許多較小的子矩陣,有時也叫塊。接下來,你就可以使用 Coppersmith 和 Winograd 的演算法,將其作為處理並最終組裝這些區塊的指導手冊。 Vassilevska Williams 說:「它告訴我在乘積矩陣 C 中要乘什麼、加什麼,以及哪些元素在哪裡。」「它只是一個從 A 和 B 建立 C 的『配方』」。
然而,這裡有一個問題:有時你會得到具有共同元素的區塊。保留這些共同元素會相當於將這些元素計算兩次,因此在某個時候,需要消除這些重疊部分。研究人員透過「消滅」它們所在的區塊來解決這個問題 —— 將它們的分量設為零以將它們從計算中移除。

Virginia Vassilevska Williams 是改良矩陣乘法新方法的團隊成員之一,她提出了目前最快的方法。
這就是 Strassen 的雷射法最終發揮作用的地方。 Le Gall 說,「雷射法通常非常有效,通常能找到消除重疊的子區塊的好方法」。在雷射消除了所有重疊之後,你就可以建立最終的乘積矩陣 C。
將這些各種技術結合起來,就得到了一種用盡量少的乘法總數來乘兩個矩陣的演算法,至少在理論上是如此。雷射法並不是為了實際應用;它只是一種思考矩陣相乘的理想方式。週任飛表示,「我們從未在電腦上運行這種方法,我們進行對它的分析。」
正是這種分析促成了 ω 十多年來的最大改進。
被發現的「隱藏損失」
在段然、週任飛和Hongxun Wu 的第一篇論文《Faster Matrix Multiplication via Asymmetric Hashing》中,他們表明,施特拉森演算法的進程可以大大加快。這一切都得益於他們稱之為「隱藏損失」(hidden loss)的概念。週任飛表示,該概念深深地隱藏在先前的分析中,是無意中消除了太多塊的結果。
雷射法的工作原理是將重疊的區塊標記為垃圾,並安排處理,而其他區塊被認為有價值並將被保存。不過,選擇過程有些隨機。事實上,被標記為垃圾的區塊可能最終還是有用的。
這並不完全令人驚訝,但透過檢查許多隨機選擇,段然團隊確定雷射法系統性地低估了區塊的價值,因此應該保存更多的區塊,減少丟棄的區塊。而且,正如通常的情況一樣,更少的浪費可以轉化為更高的效率。
對於段然團隊的做法,Le Gall 認為,「能夠保留更多區塊而不重疊,這種做法實現了更快的矩陣乘法演算法。」
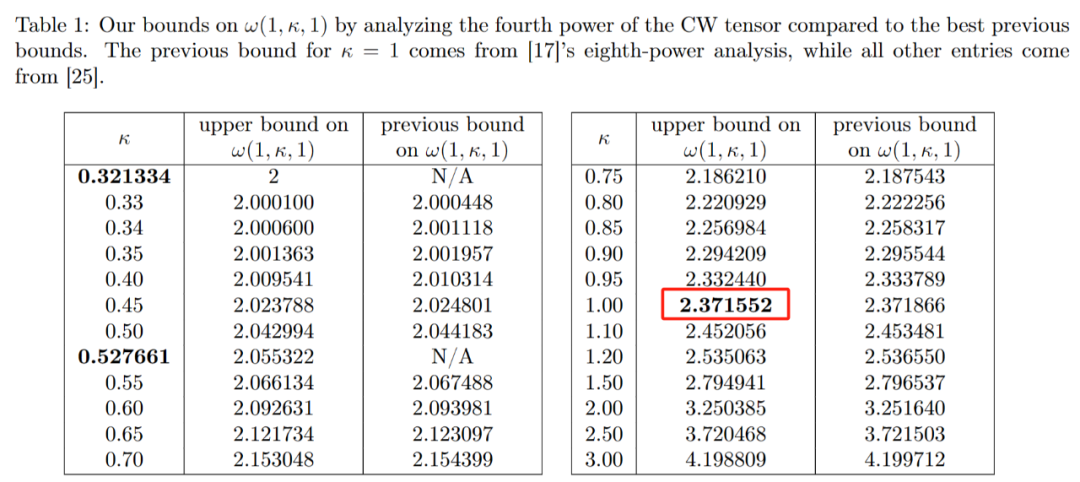
在證明了這種損失的存在後,段然團隊修改了雷射法標記塊的方式,從而大大減少了浪費。他們將 ω 的新上限設定在了 2.371866 左右,這要比 Josh Alman 和 Vassilevska Williams 在 2020 年設定的上限 2.3728596 有所改進。
這看起來是一個不大的變化,將上限降低了大約 0.001,但這是自 2010 年以來科學家們看到的最大進步。相較之下,Vassilevska Williams 和 Alman 2020 年的結果只比先前的結果提高了 0.00001。
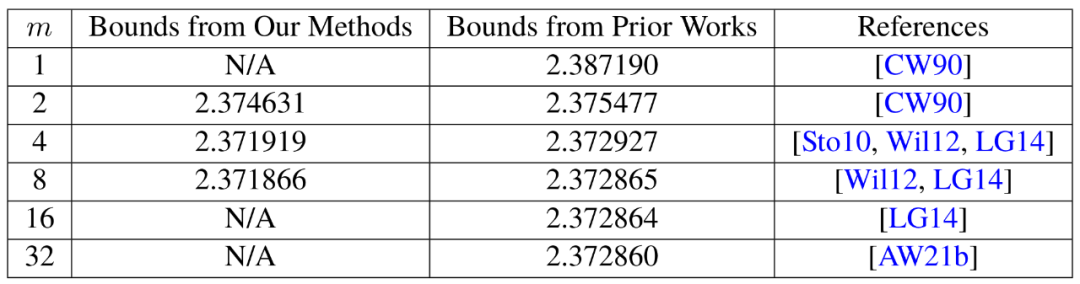
當然,對研究人員來說,最令人興奮的不僅僅是新紀錄本身,該記錄並沒有持續多久。事實上,這篇論文揭示了一種新的改進途徑,而在此之前,這種途徑完全沒有被注意到。
Le Gall 稱,近四十年來,每個人都依賴相同的雷射法。隨著段然等三位研究者的論文出現,我們可以做得更好。
因此,週任飛參與撰寫的 2024 年 1 月的論文改善了這種新方法,進一步減少了隱藏損失。他們又進一步提高了 ω 的上限,使它降低到了 2.371552。
研究者也使用同樣的方法來改進矩形(n×m)矩陣的乘法過程,該乘法過程在圖論、機器學習和其他領域均有廣泛應用。
沿著這些方向取得一些進一步的進展幾乎是肯定的,但這是有限的。 2015 年,Le Gall 和兩位合作者證明,目前的方法,也就是雷射法,再加上 Coppersmith 和 Winograd 的方法,無法得到低於 2.3078 的 ω。
Le Gall 說:「要想進一步改進,就必須在Coppersmith and Winograd 的原始方法基礎上加以改進,而這種方法自1987 年以來就沒有真正改變過。」但到目前為止,還沒有人提出更好的方法。也許根本就沒有。
週任飛說:「改進ω 其實是理解這個問題的一部分。如果我們能很好地理解這個問題,就能設計出更好的演算法。不過,人們對這個古老問題的理解還處於非常初級的階段。」
原文連結:
#https://www.quantamagazine.org/new-breakthrough-brings- matrix-multiplication-closer-to-ideal-20240307/
以上是清華姚班本科生連發兩作,十年來最大改進:矩陣乘法接近理論最優的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 ControlNet作者又出爆款!一張圖生成繪畫全過程,兩天狂攬1.4k Star
Jul 17, 2024 am 01:56 AM
ControlNet作者又出爆款!一張圖生成繪畫全過程,兩天狂攬1.4k Star
Jul 17, 2024 am 01:56 AM
同樣是圖生視頻,PaintsUndo走出了不一樣的路線。 ControlNet作者LvminZhang又開始整活了!這次瞄準繪畫領域。新項目PaintsUndo剛上線不久,就收穫1.4kstar(還在瘋狂漲)。項目地址:https://github.com/lllyasviel/Paints-UNDO透過這個項目,用戶輸入一張靜態圖像,PaintsUndo就能自動幫你生成整個繪畫的全過程視頻,從線稿到成品都有跡可循。繪製過程,線條變化多端甚是神奇,最終視頻結果和原始圖像非常相似:我們再來看一個完整的繪
 登頂開源AI軟體工程師榜首,UIUC無Agent方案輕鬆解決SWE-bench真實程式設計問題
Jul 17, 2024 pm 10:02 PM
登頂開源AI軟體工程師榜首,UIUC無Agent方案輕鬆解決SWE-bench真實程式設計問題
Jul 17, 2024 pm 10:02 PM
AIxiv專欄是本站發布學術、技術內容的欄位。過去數年,本站AIxiv專欄接收通報了2,000多篇內容,涵蓋全球各大專院校與企業的頂尖實驗室,有效促進了學術交流與傳播。如果您有優秀的工作想要分享,歡迎投稿或聯絡報道。投稿信箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com這篇論文的作者皆來自伊利諾大學香檳分校(UIUC)張令明老師團隊,包括:StevenXia,四年級博士生,研究方向是基於AI大模型的自動代碼修復;鄧茵琳,四年級博士生,研究方
 從RLHF到DPO再到TDPO,大模型對齊演算法已經是「token-level」
Jun 24, 2024 pm 03:04 PM
從RLHF到DPO再到TDPO,大模型對齊演算法已經是「token-level」
Jun 24, 2024 pm 03:04 PM
AIxiv專欄是本站發布學術、技術內容的欄位。過去數年,本站AIxiv專欄接收通報了2,000多篇內容,涵蓋全球各大專院校與企業的頂尖實驗室,有效促進了學術交流與傳播。如果您有優秀的工作想要分享,歡迎投稿或聯絡報道。投稿信箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com在人工智慧領域的發展過程中,對大語言模型(LLM)的控制與指導始終是核心挑戰之一,旨在確保這些模型既強大又安全地服務人類社會。早期的努力集中在透過人類回饋的強化學習方法(RL
 arXiv論文可以發「彈幕」了,史丹佛alphaXiv討論平台上線,LeCun按讚
Aug 01, 2024 pm 05:18 PM
arXiv論文可以發「彈幕」了,史丹佛alphaXiv討論平台上線,LeCun按讚
Aug 01, 2024 pm 05:18 PM
乾杯!當論文討論細緻到詞句,是什麼體驗?最近,史丹佛大學的學生針對arXiv論文創建了一個開放討論論壇——alphaXiv,可以直接在任何arXiv論文之上發布問題和評論。網站連結:https://alphaxiv.org/其實不需要專門訪問這個網站,只需將任何URL中的arXiv更改為alphaXiv就可以直接在alphaXiv論壇上打開相應論文:可以精準定位到論文中的段落、句子:右側討論區,使用者可以發表問題詢問作者論文想法、細節,例如:也可以針對論文內容發表評論,例如:「給出至
 OpenAI超級對齊團隊遺作:兩個大模型博弈一番,輸出更好懂了
Jul 19, 2024 am 01:29 AM
OpenAI超級對齊團隊遺作:兩個大模型博弈一番,輸出更好懂了
Jul 19, 2024 am 01:29 AM
如果AI模型給的答案一點也看不懂,你敢用嗎?隨著機器學習系統在更重要的領域中得到應用,證明為什麼我們可以信任它們的輸出,並明確何時不應信任它們,變得越來越重要。獲得對複雜系統輸出結果信任的一個可行方法是,要求系統對其輸出產生一種解釋,這種解釋對人類或另一個受信任的系統來說是可讀的,即可以完全理解以至於任何可能的錯誤都可以被發現。例如,為了建立對司法系統的信任,我們要求法院提供清晰易讀的書面意見,解釋並支持其決策。對於大型語言模型來說,我們也可以採用類似的方法。不過,在採用這種方法時,確保語言模型生
 黎曼猜想显著突破!陶哲轩强推MIT、牛津新论文,37岁菲尔兹奖得主参与
Aug 05, 2024 pm 03:32 PM
黎曼猜想显著突破!陶哲轩强推MIT、牛津新论文,37岁菲尔兹奖得主参与
Aug 05, 2024 pm 03:32 PM
最近,被稱為千禧年七大難題之一的黎曼猜想迎來了新突破。黎曼猜想是數學中一個非常重要的未解決問題,與素數分佈的精確性質有關(素數是那些只能被1和自身整除的數字,它們在數論中扮演著基礎性的角色)。在當今的數學文獻中,已有超過一千個數學命題以黎曼猜想(或其推廣形式)的成立為前提。也就是說,黎曼猜想及其推廣形式一旦被證明,這一千多個命題將被確立為定理,對數學領域產生深遠的影響;而如果黎曼猜想被證明是錯誤的,那麼這些命題中的一部分也將隨之失去其有效性。新的突破來自MIT數學教授LarryGuth和牛津大學
 LLM用於時序預測真的不行,連推理能力都沒用到
Jul 15, 2024 pm 03:59 PM
LLM用於時序預測真的不行,連推理能力都沒用到
Jul 15, 2024 pm 03:59 PM
語言模型真的能用於時序預測嗎?根據貝特里奇頭條定律(任何以問號結尾的新聞標題,都能夠用「不」來回答),答案應該是否定的。事實似乎也果然如此:強大如斯的LLM並不能很好地處理時序資料。時序,即時間序列,顧名思義,是指一組依照時間發生先後順序排列的資料點序列。在許多領域,時序分析都很關鍵,包括疾病傳播預測、零售分析、醫療和金融。在時序分析領域,近期不少研究者都在研究如何使用大型語言模型(LLM)來分類、預測和偵測時間序列中的異常。這些論文假設擅長處理文本中順序依賴關係的語言模型也能泛化用於時間序
 首個基於Mamba的MLLM來了!模型權重、訓練程式碼等已全部開源
Jul 17, 2024 am 02:46 AM
首個基於Mamba的MLLM來了!模型權重、訓練程式碼等已全部開源
Jul 17, 2024 am 02:46 AM
AIxiv专栏是本站发布学术、技术内容的栏目。过去数年,本站AIxiv专栏接收报道了2000多篇内容,覆盖全球各大高校与企业的顶级实验室,有效促进了学术交流与传播。如果您有优秀的工作想要分享,欢迎投稿或者联系报道。投稿邮箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com。引言近年来,多模态大型语言模型(MLLM)在各个领域的应用取得了显著的成功。然而,作为许多下游任务的基础模型,当前的MLLM由众所周知的Transformer网络构成,这种网






