這是數學中最著名的未解問題之一。新的工作已通過同行評審，全文可看。
最近幾天，數學圈內人們正在熱烈討論納維- 斯托克斯問題的正則哈密頓公式終於出現了—— 這個數學史上懸而未決的問題可能有了解答。而在以前，人們甚至普遍認為這是不可能的。 此事有多重要？納維 - 斯托克斯方程式與黎曼猜想一樣，在 2000 年被列為「千禧年數學七大難題」。 這七個世界級難題分別是：NP 完全問題、霍奇猜想、龐加萊猜想、黎曼假設、楊- 米爾斯存在性與品質間隙、納衛爾- 斯托克斯方程式、BSD 猜想。七個問題都懸賞一百萬美元，20 多年來只有「龐加萊猜想」被俄羅斯天才數學家佩雷爾曼解決。 它們大多讓人耳熟能詳，但「納維 - 斯托克斯方程式」（N-S 方程式）在其中似乎較少被人們提及。究其原因，可能是因為這個問題實在太難理解了（大學上過《流體力學》這門課的同學一定會有概念）。有人甚至認為，它是數學史上最複雜的公式。 簡單來說，十八世紀數學家歐拉在《流體運動的一般原理》中根據無黏性流體運動時流體所受的力和動量變化推導出了一組方程式。 歐拉方程式的描述將流體運動規定在了一個理想化世界中，但真正的流體內部是有摩擦的。自然界的流體都有黏性，統稱為黏性流體或實際流體。例如我們攪拌蜂蜜時會感受到黏滯的作用，而飛機飛行所受的阻力也很大程度來自空氣的黏性。 由於實際流體的黏性，我們對於流體運動的研究就變得非常複雜了。 在19 世紀，法國工程師兼物理學家克勞德- 路易・納維、愛爾蘭物理學和數學家喬治・斯托克斯兩人考慮分子間作用力，建立了流體平衡和運動的基本方程，並描述了運動在直角座標中的分量形式。 納維 - 斯托克斯方程式被用來描述像液體和空氣這樣的流體物質。這些方程式建立了流體的粒子動量的改變率（力）和作用在液體內部的壓力的變化和耗散粘滯力（類似於摩擦力）以及引力之間的關係。這些黏滯力產生於分子的相互作用，能告訴我們液體有多黏。這樣，納維 - 斯托克斯方程式描述作用於液體任意給定區域的力的動態平衡。 如果納維- 斯托克斯問題有全局解的話，很多與流體力學有關的技術都會出現突破，包括但不限於航空航天、火箭發動機、天氣預測、管線運輸、醫療血流建模等等。 關於這組方程式所涉及的難題在於：我們該如何用數學理論來闡明它。甚至於用數學理論解釋描述奇特黑洞的愛因斯坦場方程式都會比闡述納維 - 斯托克斯方程式更簡單一些。The important breakthrough people mentioned comes from the paper "A canonical Hamiltonian formulation of the Navier–Stokes problem", which was published in the top journal in the field of fluid mechanics on April 1 Journal of Fluid Mechanics": Paper link: https://www.cambridge.org/core/journals/journal-of-fluid -mechanics/article/canonical-hamiltonian-formulation-of-the-navierstokes-problem/B3EB9389AE700867A6A3EA63A45E69C6This paper proposes a method based on the least squares principle Derivation of a novel Hamiltonian formulation of the isotropic Navier-Stokes problem based on the minimum action principle. The formula uses velocity
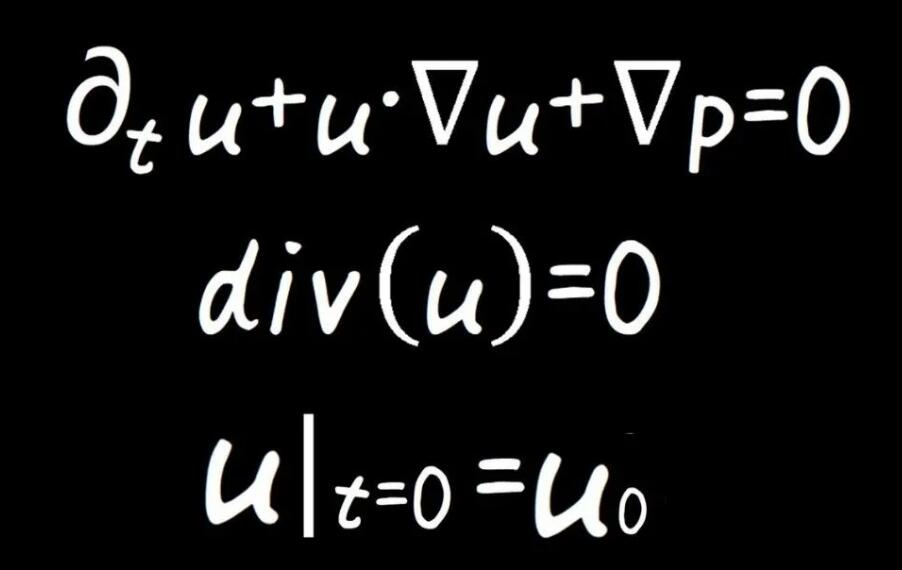
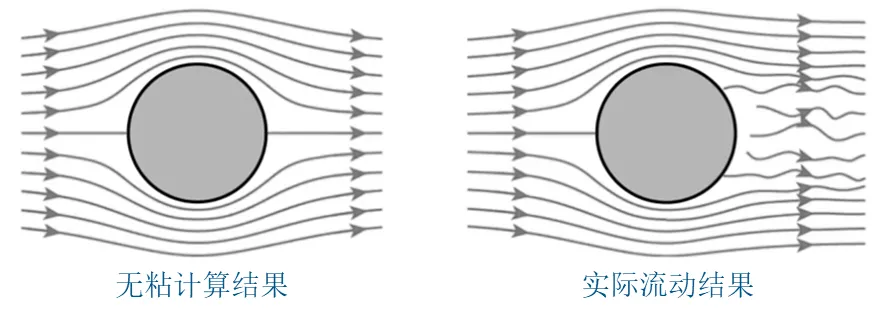
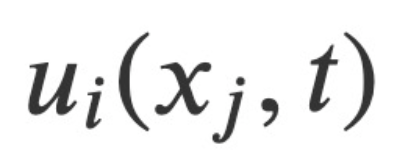and pressure
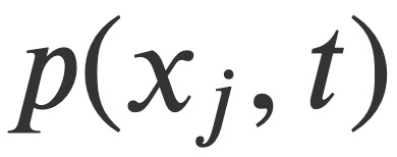as variable field quantities, as well as the canonical conjugate momentum derived from analysis. Based on this, this study constructs a conserved Hamiltonian function H* that satisfies the Hamiltonian canonical equation, and formulates the related Hamiltonian-Jacobian equations for compressible and incompressible flows. This Hamiltonian-Jacobian equation reduces the problem of finding four independent field quantities to finding a single scalar functional among these fields - Hamilton's main functional. Furthermore, Hamilton and Jacobi's transformation theory provides a prescribed method for solving the Navier-Stokes problem: find S*.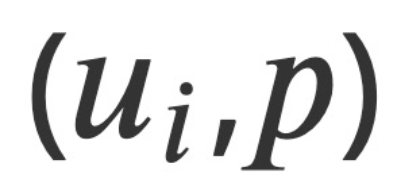 
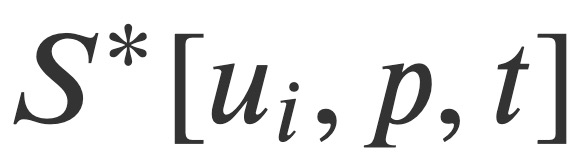
If the analytical expression of S * can be obtained, then it will obtain a set of new fields through regular transformation, giving the analytical expressions of the original velocity and pressure fields, These fields will simply be equivalent to their initial values. Failing that, one can only prove that a complete solution to the Hamilton-Jacobian equation exists or does not exist, which would also solve the problem of the existence of the solution.
Could this new research lead to a million-dollar prize? To win, researchers must show that there are solutions to the three-dimensional incompressible Navier-Stokes equations and that, if there are solutions, those solutions are smooth.
Mathematician Terence Tao once thought that this was difficult. 
Judging from the current progress, new research has made it easier to solve open problems, and we have taken a big step forward - Navier-Stor The canonical Hamiltonian formulation of the Kers equation may mean that we can bypass the limitations of the standard Lagrangian and reduce the problem to finding a single scalar function.
Perhaps we are not far away from solving the second question of the Millennium Puzzle. https://www1.grc. nasa.gov/beginners-guide-to-aeronautics/navier-strokes-equation/https://zhuanlan.zhihu.com/p/263628141https://terrytao.wordpress.com/2007/03/18/why-global-regularity-for-navier-stokes-is-hard/以上是N-S方程式問題有解了？與黎曼猜想並列，千禧年數學難題勝利在望的詳細內容。更多資訊請關注PHP中文網其他相關文章！
