
AIxiv專欄是本站發布學術、技術內容的欄位。過去數年,本站AIxiv專欄接收通報了2,000多篇內容,涵蓋全球各大專院校與企業的頂尖實驗室,有效促進了學術交流與傳播。如果您有優秀的工作想要分享,歡迎投稿或聯絡報道。投稿信箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com。
從國際頂流GPT-4 128K、Claude 200K 到國內「紅炸子雞」支援200 萬字以上文本的Kimi Chat,大語言模型(LLM)在長上下文技術上不約而同地捲起了。當全世界最聰明的頭腦都在卷一件事的時候,這件事的重要性和難度就自然不言自明。
極長的脈絡可以極大拓展大模型的生產力價值。 隨著 AI 的普及,使用者不再滿足於調戲大模型幾個腦筋急轉彎,使用者開始渴望利用大模型來真正提高生產力。畢竟從前花一周憋出來的 PPT,現在只需要餵給大模型一串提示詞和幾份參考文檔就分分鐘生成出來,打工人誰能不愛呢?
最近出現了一些新型高效能序列建模方法,例如Lightning Attention (TransNormerLLM)、State Space Modeling (Mamba)、Linear RNN (RWKV, HGRN, Griffin)等,成為炙手可熱的研究方向。研究人員渴望透過改造已經成熟的7歲高齡的Transformer架構,獲得效能與之旗鼓相當,但複雜度僅為線性的新型架構。這類方法專注於模型架構設計,並提供了基於CUDA或Triton的硬體友好實現,使其能夠像FlashAttention一樣在單卡GPU內部高效計算。
同時,另一個長序列訓練的控制者也採取了不同的策略:序列並行獲取了越來越多的關注。透過將長序列在序列維度切割成多個等分短序列,並將短序列分散至不同 GPU 卡並行訓練,再輔以卡間通訊便達到了序列並行訓練的效果。從最早出現的 Colossal-AI 序列並行、到 Megatron 序列並行、再到 DeepSpeed Ulysses、以及近期的 Ring Attention,研究人員不斷設計更優雅高效的通訊機制以提升序列並行的訓練效率。當然這些已知方法全部是為傳統注意力機制設計的,本文中我們稱之為 Softmax Attention。這些方法也已經有各路大神做了精彩分析,本文不過多探討。

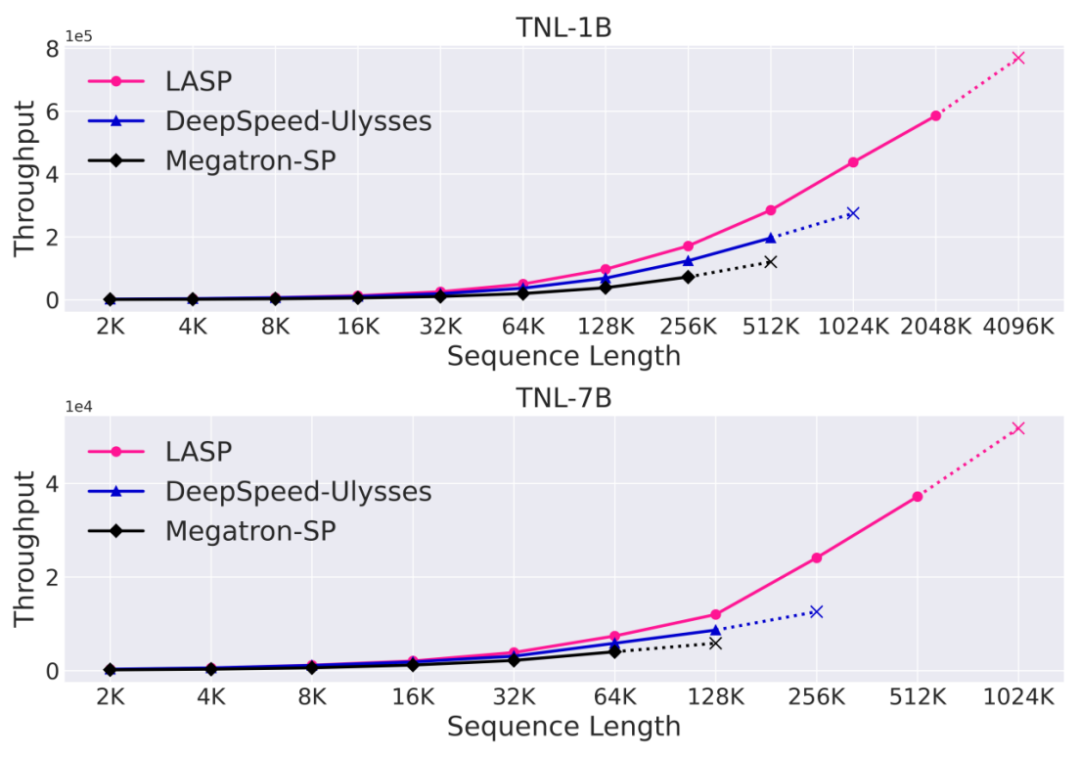
#本文即將介紹的LASP 便應運而生。來自上海人工智慧實驗室的研究人員提出了 Linear Attention Sequence Parallelism(LASP)方法以充分利用 Linear Attention 的線性右乘特性實現高效的序列平行運算。在 128 卡 A100 80G GPU、TransNormerLLM 1B 模型、FSDP backend 的配置下,LASP 可以將序列長度最高擴展至 4096K,即 4M。與成熟的序列平行方法相比,LASP 可訓練的最長序列長度是 Megatron-SP 的 8 倍、DeepSpeed Ulysses 的 4 倍,速度則分別快了 136% 和 38%。
要注意的是,自然語言處理方法的名稱包含Linear Attention,但不限於Linear Attention方法,而是可廣泛應用於包括Lightning Attention (TransNormerLLM)、State Space Modeling (Mamba )、Linear RNN (RWKV、HGRN、Griffin)等在內的線性序列建模方法。
LASP 方法介紹
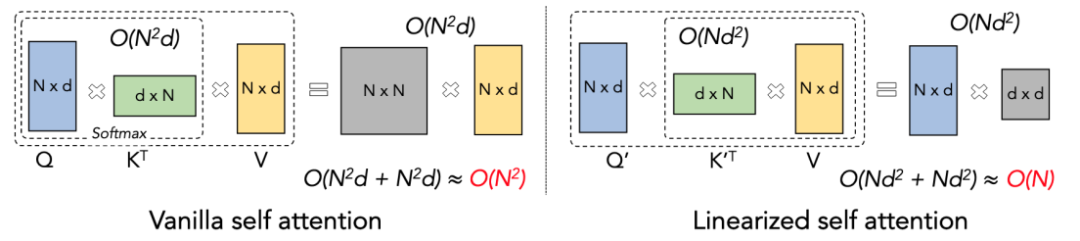
#為了更能理解LASP的思路,讓我們先回顧一下傳統Softmax Attention的計算公式:O=softmax((QK^T)⊙M)V,其中Q、K、V、M、O 分別為Query、Key、Value、Mask 和Output 矩陣,這裡的M 在單向任務(如GPT)中是一個下三角的全1 矩陣,在雙向任務(如BERT)中則可忽略,即雙向任務沒有Mask 矩陣。我們將LASP拆分為四點來解釋:
Linear Attention 原理
Linear Attention 可視為 Softmax Attention 一種變體。 Linear Attention 移除了計算成本高昂的 Softmax 算子,Attention 的計算公式可以寫為 O=((QK^T)⊙M) V 的簡潔形式。但由於單向任務中 Mask 矩陣 M 的存在,使得該形式依然只能進行左乘計算(即先計算 QK^T),因此無法獲得 O (N) 的線性複雜度。但對於雙向任務,由於沒有 Mask 矩陣的存在,其計算公式可以進一步簡化為 O=(QK^T) V。 Linear Attention 的巧妙之處在於,僅利用簡單的矩陣乘法結合律,其計算公式就可以進一步轉化為:O=Q (K^T V),這種計算形式稱為右乘,可見Linear Attention 在這種雙向任務中可以達到誘人的O (N) 複雜度!
LASP 資料分發
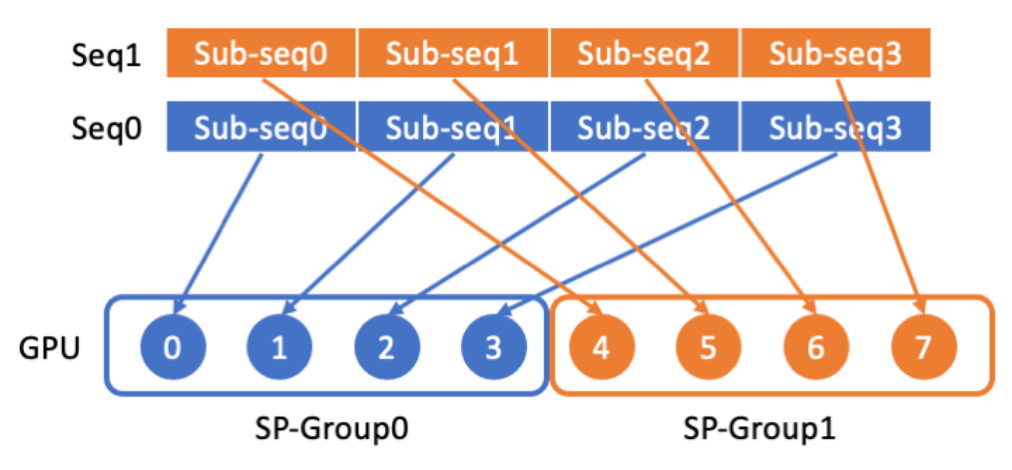
LASP 首先將長序列資料從序列維度切割成多個等分的子序列,再將子序列分散傳送至序列平行通訊群組內的所有GPU,使得每張GPU 上各有一段子序列,以供後續序列平行計算的使用。
LASP 核心機制
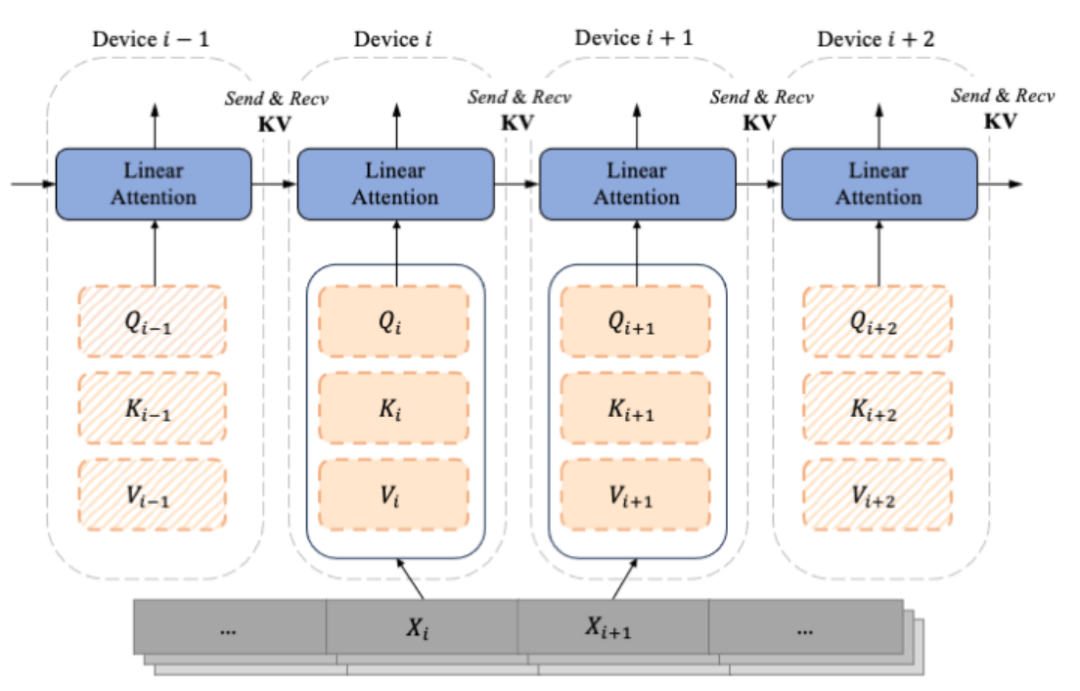
#隨著decoder-only 的類別GPT 形式的模型逐漸成為LLM 的事實標準,LASP 的設計充分考慮了單向Casual 任務的場景。由切分後子序列 Xi 計算而來的便是依照序列維度切分的 Qi, Ki, Vi,每一個索引 i 對應一個 Chunk 和一個 Device(即一張 GPU)。由於 Mask 矩陣的存在,LASP 作者巧妙地將各個 Chunk 對應的 Qi, Ki, Vi 區分為兩種,即:Intra-Chunk 和 Inter-Chunk。其中Intra-Chunk 為Mask 矩陣分塊後對角線上的Chunk,可以認為仍有Mask 矩陣的存在,仍然需要使用左乘;Inter-Chunk 則為Mask 矩陣非對角線上的Chunk,可以認為沒有Mask 矩陣的存在,可以使用右乘;顯然,當切分的Chunk 越多時,對角線上的Chunk 佔比越少,非對角線上的Chunk 佔比越多,可以利用右乘實現線性複雜度Attention 計算的Chunk 就越多。其中,對於右乘的 Inter-Chunk 的計算,前向計算時每個設備需要使用點對點通訊 Recive 上一個設備的 KV,並 Send 自己的更新後的 KV 給下一個設備。反向計算時則正好相反,只是 Send 和 Recive 的物件變成 KV 的梯度 dKV。其中前向運算流程如下圖所示:
LASP 程式碼實作
為了提高LASP 在GPU 上的運算效率,作者對Intra-Chunk 和Inter-Chunk 的計算分別進行了Kernel Fusion,並將KV 和dKV 的更新計算也融合到了Intra-Chunk 和Inter-Chunk 計算中。另外,為了在反向傳播過程中避免重新計算激活 KV,作者選擇在前向傳播計算後立即將其儲存在 GPU 的 HBM 中。在隨後的反向傳播過程中,LASP 直接存取 KV 以供使用。需要注意的是,儲存在 HBM 中的 KV 大小為 d x d,完全不受序列長度 N 的影響。當輸入序列長度 N 較大時,KV 的記憶體佔用變得微不足道。在單張 GPU 內部,作者實現了由 Triton 實現的 Lightning Attention 以減少 HBM 和 SRAM 之間的 IO 開銷,從而加速單卡 Linear Attention 運算。
想要了解更多細節的讀者,可以閱讀論文中的 Algorithm 2(LASP 前向過程)和 Algorithm 3(LASP 反向過程),以及文中詳細的推導過程。
通訊量分析
LASP 演算法中需要注意前向傳播需要在每個 Linear Attention 模組層進行 KV 激活的通訊。通訊量為 Bd^2/h,其中 B 是 batch 大小,h 是頭數。相較之下,Megatron-SP 在每個Transformer 層中的兩個Layer Norm 層之後分別使用了一次All-Gather 操作,並在Attention 和FFN 層之後分別使用了一次Reduce-Scatter 操作,這導致其通信量為2BNd 4BNd/T,其中T 為序列並行維度。 DeepSpeed-Ulysses 使用了 All-to-All 集合通訊操作來處理每個 Attention 模組層的輸入 Q, K, V 和輸出 O,導致通訊量為 4BNd/T。三者的通信量比較如下表所示。其中 d/h 是頭維度,通常設定為 128。在實際應用中,當 N/T>=32 時,LASP 便能達到最低的理論通訊量。此外,LASP 的通訊量不受序列長度 N 或子序列長度 C 的影響,這對於跨大型 GPU 叢集的極長序列並行運算是一個巨大的優勢。
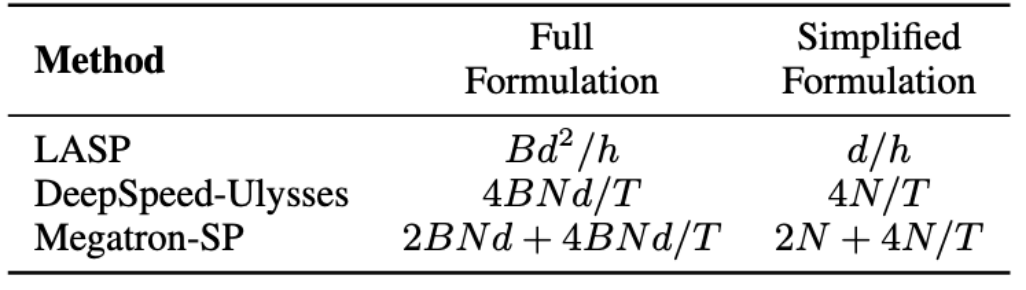
Data-Sequence 混合併行
資料並行(即Batch-level 的資料切分)已經是分散式訓練的常規操作,在原始資料並行(PyTorch DDP)的基礎上,已經進化出了更節省顯存的切片式資料並行,從最初的DeepSpeed ZeRO 系列到PyTorch 官方支援的FSDP,切片式資料並行已經足夠成熟並被越來越多用戶使用。 LASP 作為 Sequence-level 的資料切分方法,可以能夠和包含 PyTorch DDP, Zero-1/2/3, FSDP 在內的各種資料並行方法相容使用。這對 LASP 的使用者來說無疑是個好消息。
精度實驗
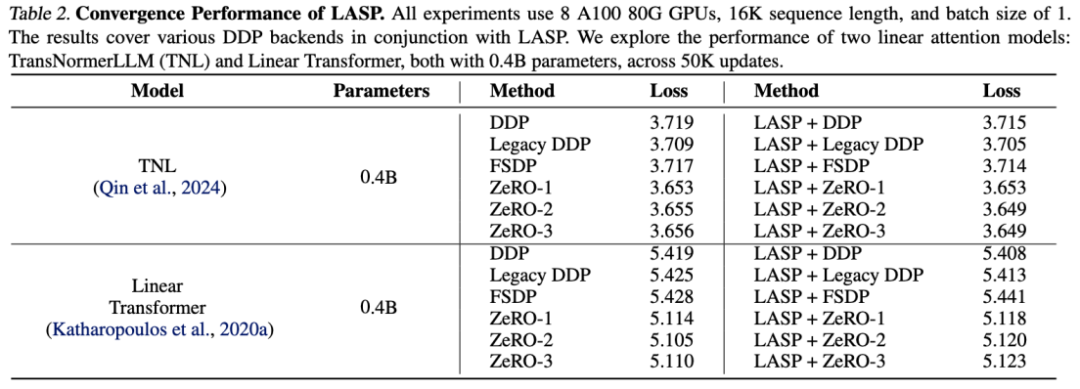
在TransNormerLLM (TNL) 和Linear Transformer 上的實驗結果表明,LASP 作為一種系統優化方法能夠和各種DDP backends 結合,並均能達到與Baseline 持平的效能。
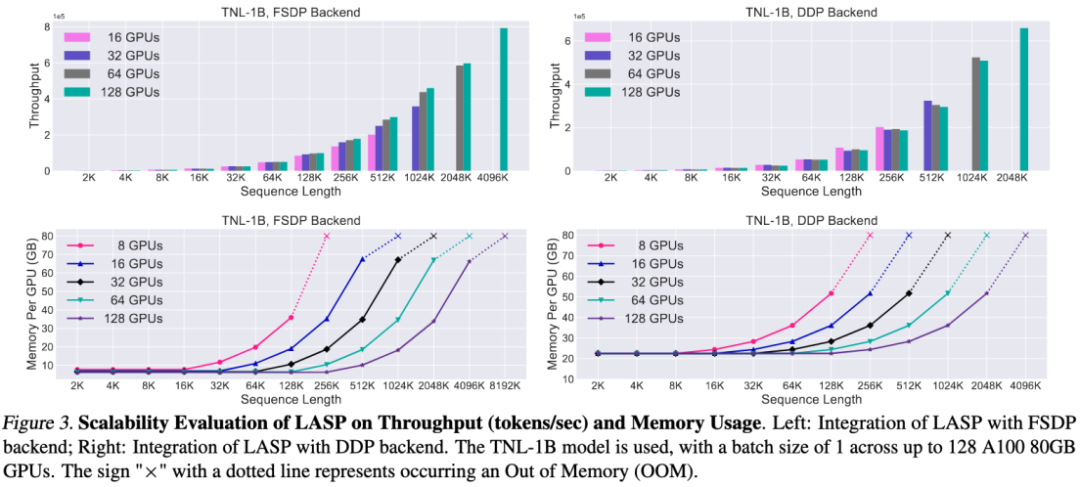
可擴展性實驗
得益於高效的通訊機制設計,LASP 可以輕鬆擴展至上百卡GPU,並保持很好的可擴展性。
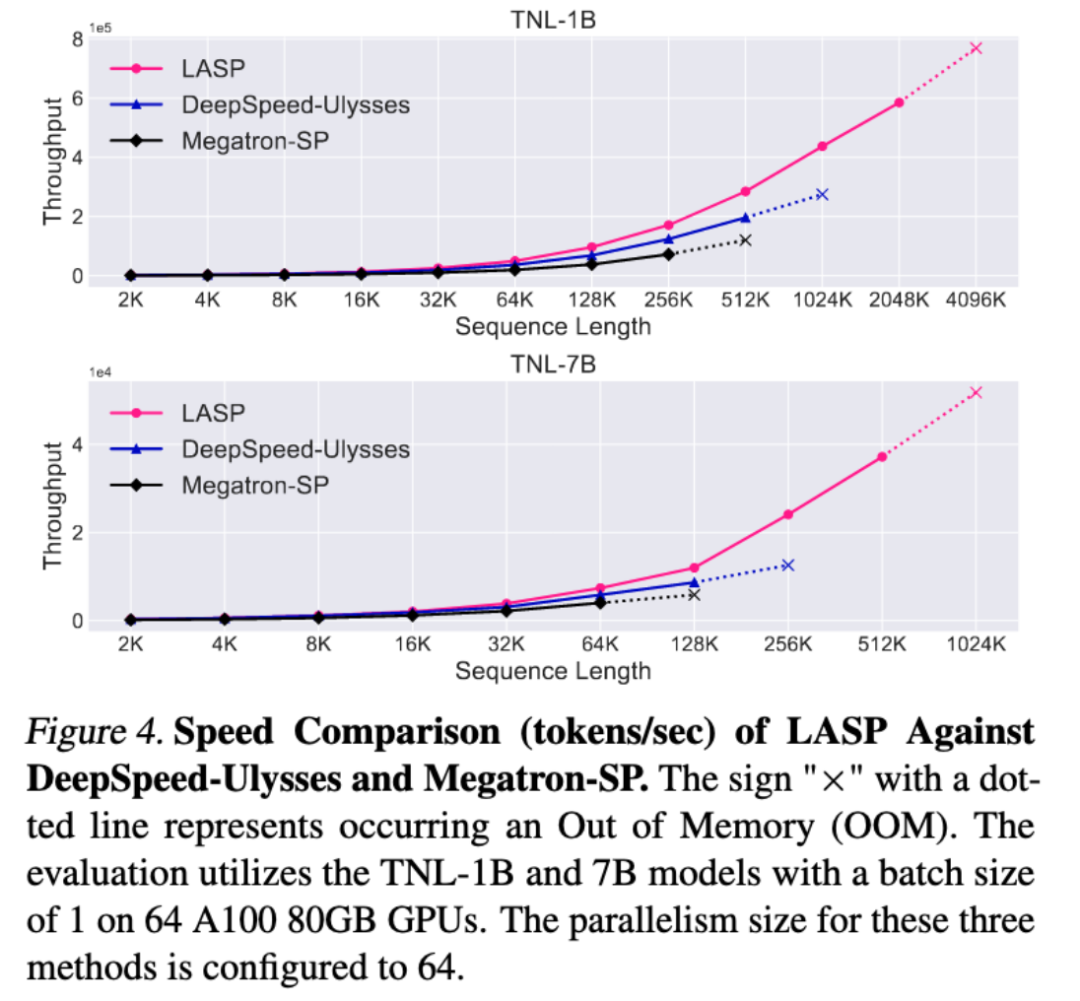
速度對比實驗
與成熟的序列並行方法Megatron-SP 和DeepSpeed-Ulysses 對比,LASP 可訓練的最長序列長度是Megatron-SP 的8 倍、DeepSpeed-Ulysses 的4 倍,速度則分別快了136% 和38%。
結論
為了方便大家試用,作者已經提供了一個即裝即用的LASP 程式碼實現,無需下載數據集合和模型,只需PyTorch 分分鐘體驗LASP 的極長極快序列並行能力。
程式碼傳送門:https://github.com/OpenNLPLab/LASP
以上是極長序列、極快速度:面向新一代高效大語言模型的LASP序列並行的詳細內容。更多資訊請關注PHP中文網其他相關文章!




