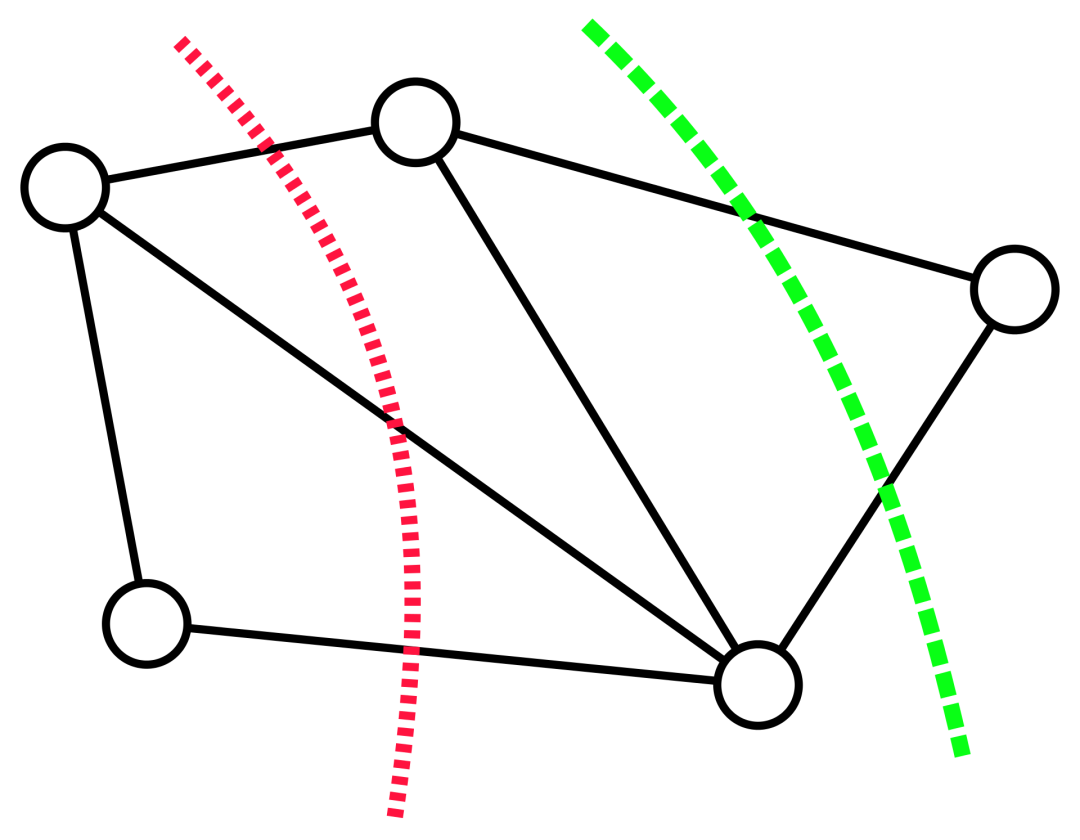
無向圖最小割問題新突破,Google研究獲SODA 2024最佳論文獎
Блог Google опубликовал новое исследование, направленное на решение проблемы минимального сечения неориентированных графов.

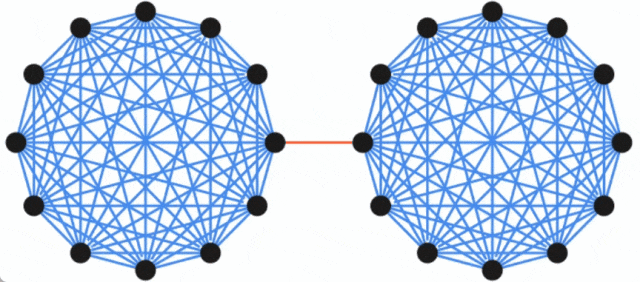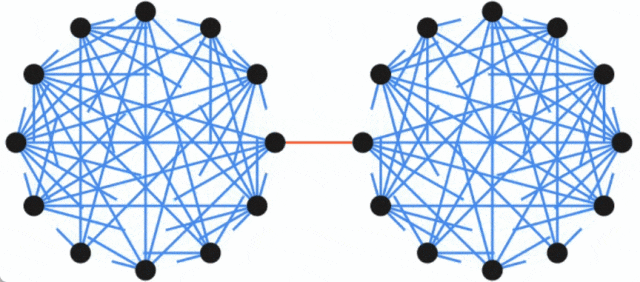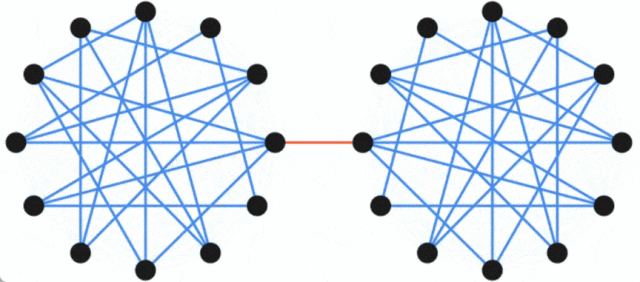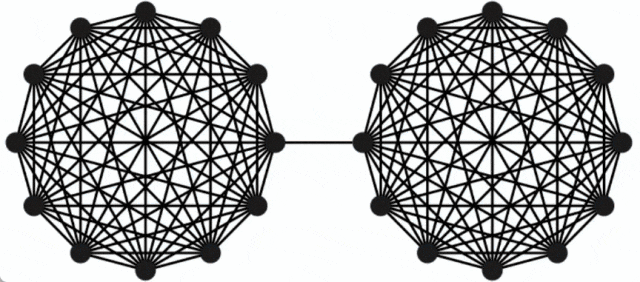
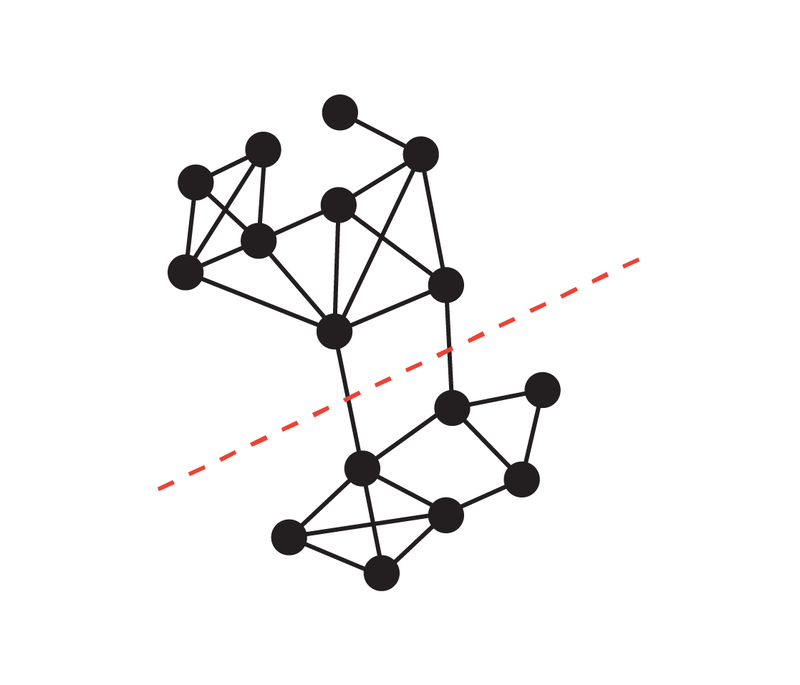
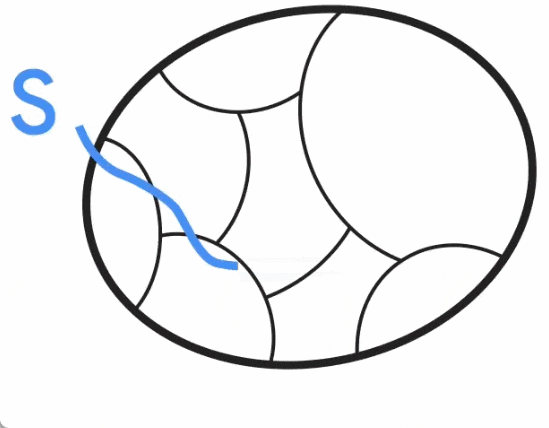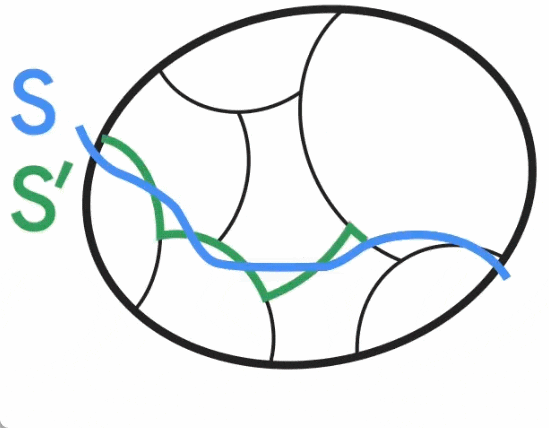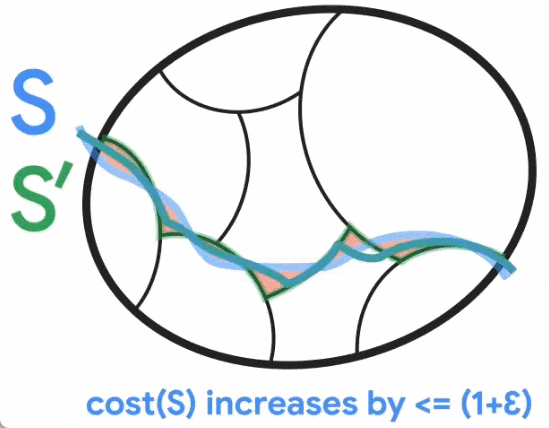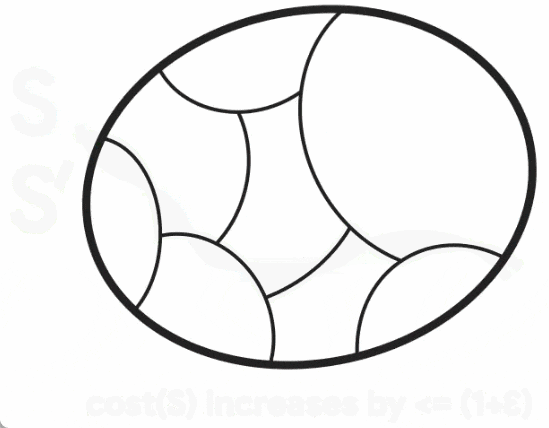
以上是無向圖最小割問題新突破,Google研究獲SODA 2024最佳論文獎的詳細內容。更多資訊請關注PHP中文網其他相關文章!

熱AI工具

Undresser.AI Undress
人工智慧驅動的應用程序,用於創建逼真的裸體照片

AI Clothes Remover
用於從照片中去除衣服的線上人工智慧工具。

Undress AI Tool
免費脫衣圖片

Clothoff.io
AI脫衣器

Video Face Swap
使用我們完全免費的人工智慧換臉工具,輕鬆在任何影片中換臉!

熱門文章

熱工具

記事本++7.3.1
好用且免費的程式碼編輯器

SublimeText3漢化版
中文版,非常好用

禪工作室 13.0.1
強大的PHP整合開發環境

Dreamweaver CS6
視覺化網頁開發工具

SublimeText3 Mac版
神級程式碼編輯軟體(SublimeText3)
 芝麻開門交易所網頁版登入口 最新版gateio官網入口
Mar 04, 2025 pm 11:48 PM
芝麻開門交易所網頁版登入口 最新版gateio官網入口
Mar 04, 2025 pm 11:48 PM
詳細介紹芝麻開門交易所網頁版登入口操作,含登錄步驟、找回密碼流程,還針對登錄失敗、無法打開頁面、收不到驗證碼等常見問題提供解決方法,助你順利登錄平台。
 芝麻開門交易所網頁註冊鏈接 gate交易app註冊網址最新
Feb 28, 2025 am 11:06 AM
芝麻開門交易所網頁註冊鏈接 gate交易app註冊網址最新
Feb 28, 2025 am 11:06 AM
本文詳細介紹了芝麻開門交易所(Gate.io)網頁版和Gate交易App的註冊流程。 無論是網頁註冊還是App註冊,都需要訪問官方網站或應用商店下載正版App,然後填寫用戶名、密碼、郵箱和手機號等信息,並完成郵箱或手機驗證。
 加密數字資產交易APP推薦top10(2025全球排名)
Mar 18, 2025 pm 12:15 PM
加密數字資產交易APP推薦top10(2025全球排名)
Mar 18, 2025 pm 12:15 PM
本文推荐十大值得关注的加密货币交易平台,涵盖币安(Binance)、OKX、Gate.io、BitFlyer、KuCoin、Bybit、Coinbase Pro、Kraken、BYDFi和XBIT去中心化交易所。这些平台在交易币种数量、交易类型、安全性、合规性、特色功能等方面各有千秋,例如币安以其全球最大的交易量和丰富的功能著称,而BitFlyer则凭借其日本金融厅牌照和高安全性吸引亚洲用户。选择合适的平台需要根据自身交易经验、风险承受能力和投资偏好进行综合考量。 希望本文能帮助您找到最适合自
 歐易okex賬號怎麼註冊、使用、註銷教程
Mar 31, 2025 pm 04:21 PM
歐易okex賬號怎麼註冊、使用、註銷教程
Mar 31, 2025 pm 04:21 PM
本文詳細介紹了歐易OKEx賬號的註冊、使用和註銷流程。註冊需下載APP,輸入手機號或郵箱註冊,完成實名認證。使用方面涵蓋登錄、充值提現、交易以及安全設置等操作步驟。而註銷賬號則需要聯繫歐易OKEx客服,提供必要信息並等待處理,最終獲得賬號註銷確認。 通過本文,用戶可以輕鬆掌握歐易OKEx賬號的完整生命週期管理,安全便捷地進行數字資產交易。
 如何在Bitget官網註冊並下載最新App
Mar 05, 2025 am 07:54 AM
如何在Bitget官網註冊並下載最新App
Mar 05, 2025 am 07:54 AM
本指南提供了 Bitget 交易所官方 App 的詳細下載和安裝步驟,適用於安卓和 iOS 系統。指南整合了來自多個權威來源的信息,包括官網、App Store 和 Google Play,並強調了下載和賬戶管理過程中的注意事項。用戶可以從官方渠道下載 App,包括應用商店、官網 APK 下載和官網跳轉,並完成註冊、身份驗證和安全設置。此外,指南還涵蓋了常見問題和注意事項,例如
 為什麼說Bittensor是AI賽道的'比特幣”?
Mar 04, 2025 pm 04:06 PM
為什麼說Bittensor是AI賽道的'比特幣”?
Mar 04, 2025 pm 04:06 PM
原文標題:Bittensor=AIBitcoin?原文作者:S4mmyEth,DecentralizedAIResearch原文編譯:zhouzhou,BlockBeats編者按:本文討論了Bittensor,一個去中心化的AI平台,希望通過區塊鏈技術打破集中式AI公司的壟斷,推動開放、協作的AI生態系統。 Bittensor採用子網模型,允許不同AI解決方案的出現,並通過TAO代幣激勵創新。儘管AI市場已成熟,但Bittensor面臨競爭風險,可能會受到其他開源
 binance怎麼註冊詳細教程(2025新手指南)
Mar 18, 2025 pm 01:57 PM
binance怎麼註冊詳細教程(2025新手指南)
Mar 18, 2025 pm 01:57 PM
本文提供Binance幣安註冊及安全設置的完整指南,涵蓋註冊前的準備工作(包括設備、郵箱、手機號及身份證明文件準備),詳細介紹了官網及APP兩種註冊方式,以及不同級別的身份驗證(KYC)流程。此外,文章還重點講解瞭如何設置資金密碼、開啟雙重驗證(2FA,包括谷歌身份驗證器和短信驗證)以及設置防釣魚碼等關鍵安全步驟,幫助用戶安全便捷地註冊和使用Binance幣安平台進行加密貨幣交易。 請務必在交易前了解相關法律法規及市場風險,謹慎投資。







