Lean Copilot，讓陶哲軒等眾多數學家讚不絕口的這個形式化數學工具，又有超強進化了？
就在剛剛，加州理工學院教授Anima Anandkumar宣布，團隊發布了Lean Copilot論文的擴展版本，並且更新了程式碼庫。
圖片
論文網址：https://arxiv.org/pdf/2404.12534.pdf
#最新實驗表明，這個Copilot工具，可以自動化80%以上的數學證明步驟了！這個紀錄，比以前的基線aesop還要好2.3倍。
並且，和以前一樣，它在MIT許可下是開源的。
圖片
他是華人小哥宋沛洋，他是UCSB的榮譽CS本科生，加州理工學院計算數學科學（CMS）系的SURF研究員。
網友驚呼：所以，陶哲軒現在的數學研究可以原地加速5倍了？
圖片
LLM提出證明策略，人類無縫幹預
團隊就發布了這個Lean Copilot的工具，希望啟動人類和LLM的協作，寫出100%準確的形式化數學證明。
它解決了一個核心技術挑戰：在Lean中運行LLM的推理。
透過這個工具，我們可以讓LLM在Lean中提出證明策略，讓人類以無縫的方式介入和修改。
圖片
之所以開發這個項目，是因為自動化定理證明在如今仍是一項艱鉅的挑戰。
我們都知道，LLM在做數學和推理任務時，常常會犯錯、產生幻覺，十分不可靠。
圖片
因此，到目前為止，數學證明大多是手動推導的，需要仔細驗證。
像Lean這的定理證明工具，倒是可以形式化證明過程的每一步，但人類寫起Lean，實在很費力。
在這種情況下，Lean Copilot的誕生就顯得意義重大。
讓陶哲軒多次震驚的神器：數學家還不會用就完蛋了
LLM可以作為輔助人類證明定理的工具，這論點已經被陶哲軒多次證實了。
他前腳剛在部落格預測，26年AI將和搜尋、符號數學工具結合，成為數學研究中值得信賴的合著者。
緊接著，佐證他觀點的研究就如雨後春筍一般源源不絕地冒出來。
去年6月，加州理工、英偉達、MIT等機構的學者，就建構了一個基於開源LLM的定理證明器LeanDojo。
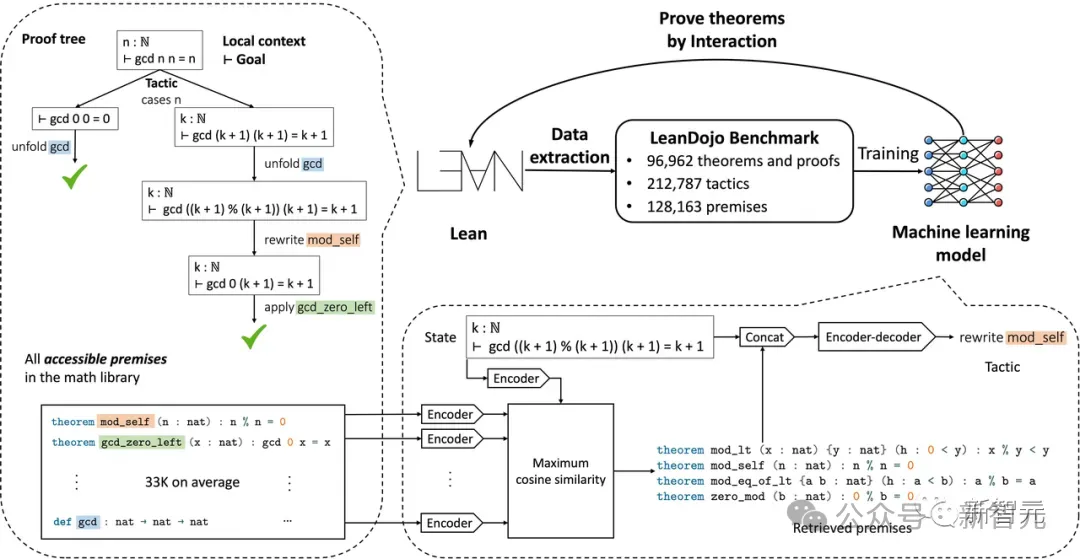圖片
9月，微軟亞洲研究院、北大、北航等機構的研究人員，透過97個回合的「蘇格拉底式」嚴格推理，成功讓GPT-4得出了「P≠NP」的結論，破解了這個千禧年難題 。
圖片
在第97輪對話中，GPT-4得出結論，證明範例在沒有窮舉法的情況下無法求解，證明了結論為P≠NP
去年10月，陶哲軒在GPT-4、Copilot的幫助下，直接發現了自己論文中的一處隱藏bug。
在用Lean4形式化第6頁論點的過程中發現，他發現表達式
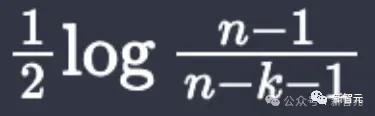圖片
在n=3,k=2時，其實是發散的。
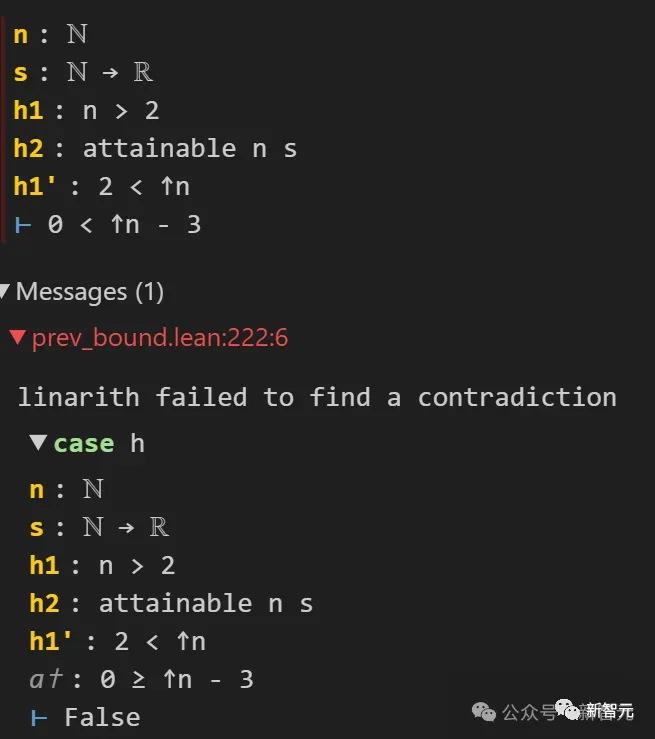
這個不太容易看出的bug能被及時抓住，多虧了Lean4。原因是，Lean要求他建構02。由此，Lean無法基於負的0
圖片
這個發現直接讓陶哲軒瞳孔震驚。
圖片
而在去年年底，#陶哲軒直接成功地用AI工具，完成了形式化多項式Freiman-Ruzsa猜想證明過程的工作。
圖片
最後，依賴關係圖已經完全被綠色所覆蓋，Lean編譯器也報告說，這個猜想完全遵循標準公理。
圖片
在這個過程中，所有最前線的數學研究者，都在第一時間感受到了AI對於數學研究顛覆力量的直接衝擊。
Lean Coilot，讓Lean更好用
而今天，Lean Copilot的這項研究，讓Lean直接變得更強大了。
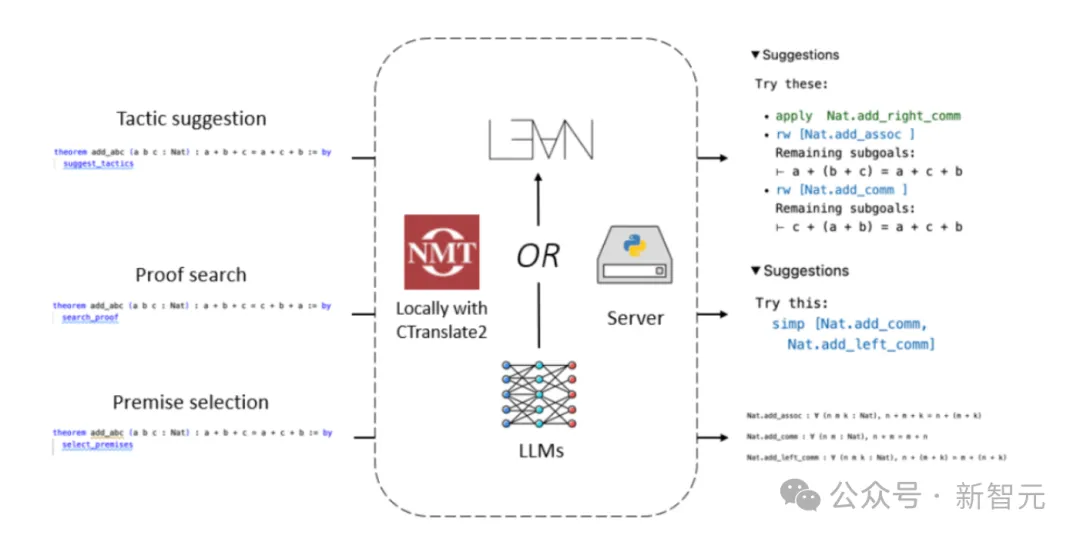
在這篇論文中，團隊基於Lean Copilot建立了一些工具，用於建議證明步驟（策略建議）、完成中間證明目標（證明搜尋）和使用LLM選擇相關前提（前提選擇）。
實驗結果也充分證明了，跟Lean中現有的基於規則的證明自動化相比，Lean Copilot在輔助人類自動化定理證明上，是有效的。
Lean Copilot提供了一個通用框架，可以透過CTranslate 2在本地，或在伺服器上執行LLM的推理。
透過這個框架，使用者就能創造各種自動化證明工具。
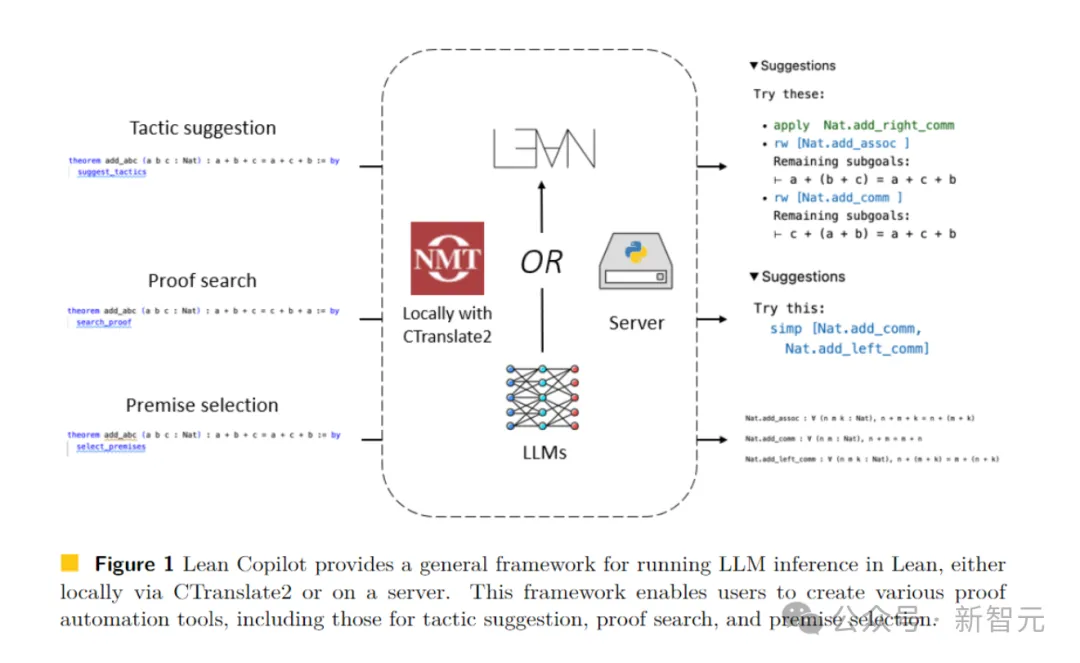圖片
Lean是數學家中很受歡迎的證明助手。如下圖所示，Lean中的一個證明，是由一系列被稱為策略（tactics）的證明步驟組成。
圖片
從整個定理開始作為初始目標，策略反覆地將目前的目標轉換為更簡單的子目標，直到所有目標都解決。
使用者在由VSCode驅動的IDE中互動編寫策略，在右邊的infoview面板中顯示目標。
產生策略建議
利用Lean Copilot，團隊建立了suggest_tropics，一種用LLM產生策略建議的工具。
而它本身，也是一種策略。
應用程式時，它會將目前目標輸入LLM，並且從LLM取得產生的策略候列表。
它會查看每個選項，看它們是否會 1）導致錯誤；2）結果沒有錯，但不能完成證明；3）順利完成證明。
如果是1），這個策略就會被刪除。
圖片
只有無錯誤的策略，才會顯示在右邊的視圖面板中。
其中，成功完成證明的策略，使用綠色標記（類別3）；沒有錯誤改變證明目標，但未完成證明的策略，使用藍色標記（類別2）。
注意！當所有列出的策略都屬於類別2時，這個資訊對於使用者來說，可能極有價值。
在這種情況下，剩餘目標的訊息，可以直接幫助使用者選擇策略，作為下一個中間證明步驟。
看到建議後，使用者可以選擇是否接受，或使用它們作為靈感來源，制定新策略。
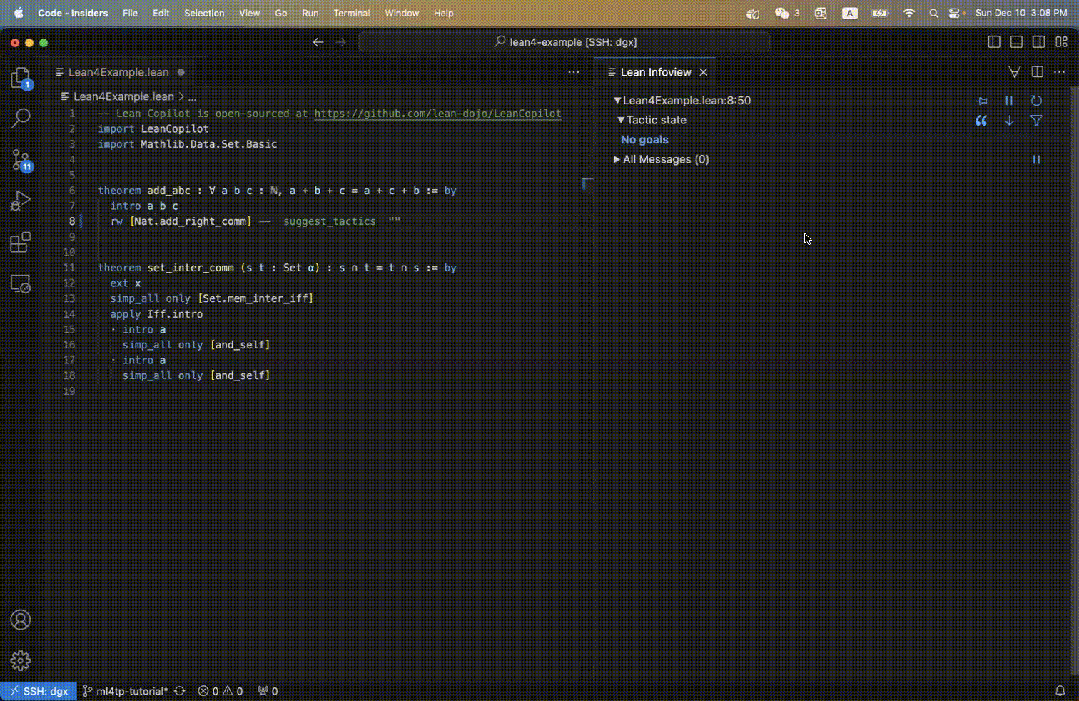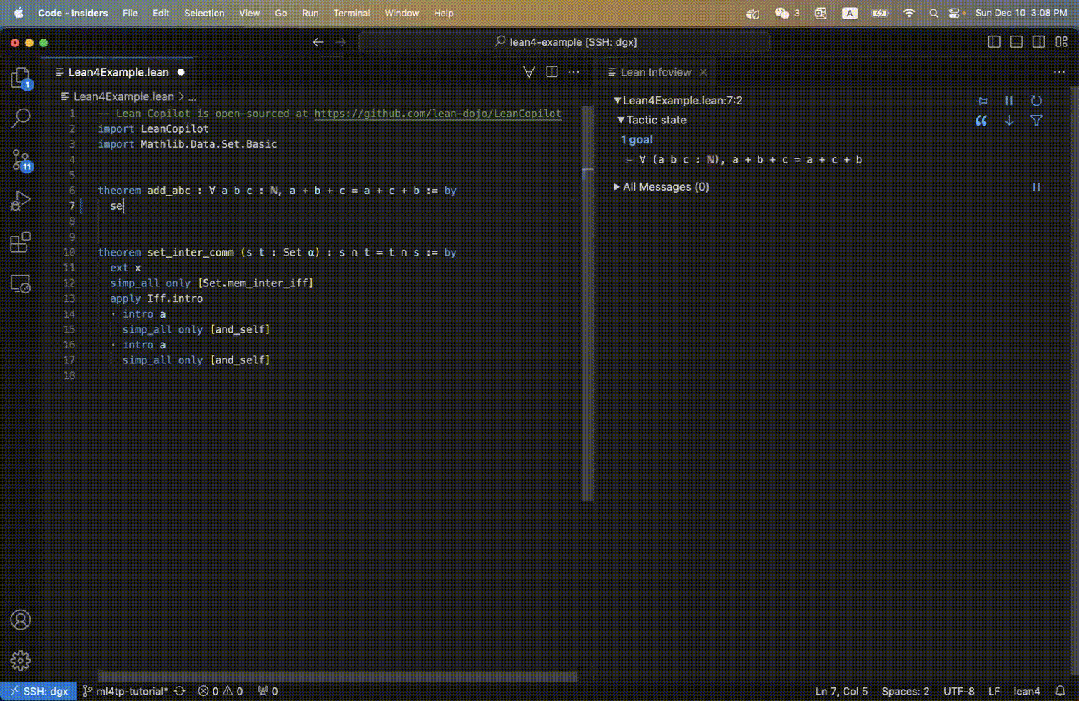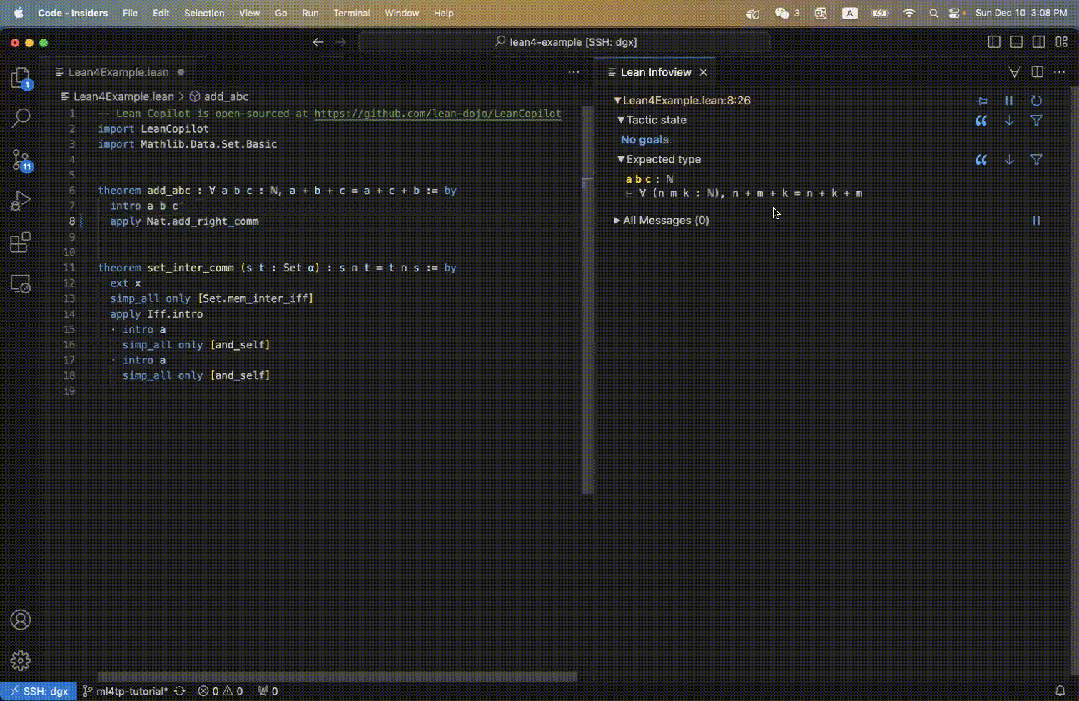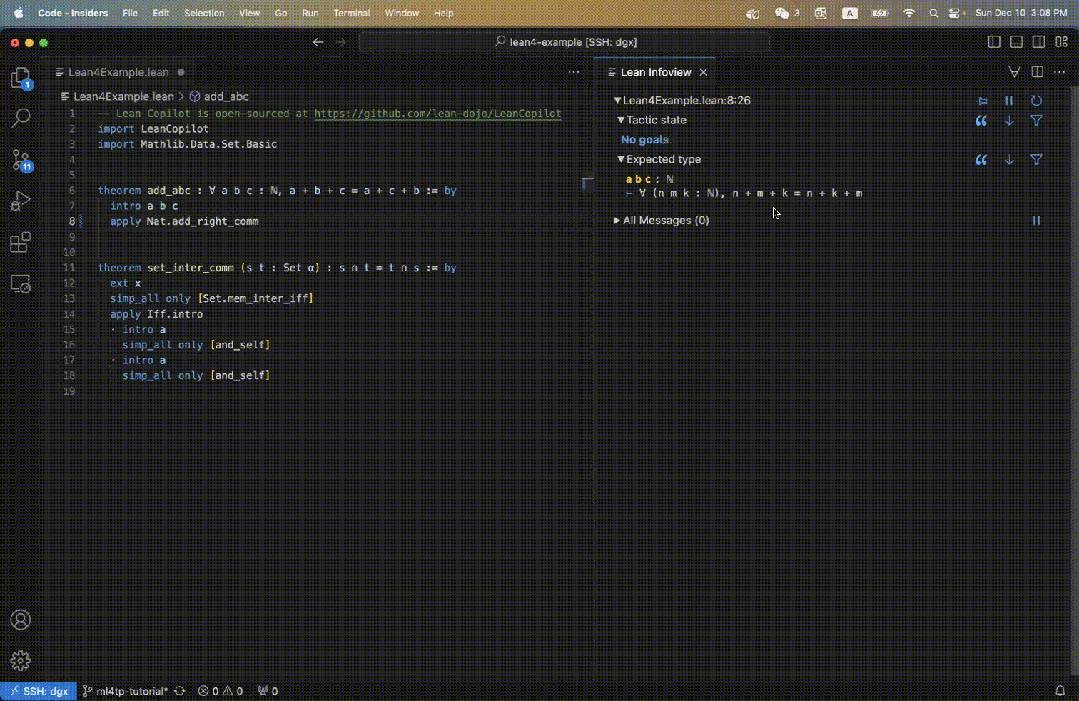
例如，我們在Lean程式碼中定義了一個定理add_abc，它的初始目標如圖3右所示。
圖片
當我們輸入suggest_tropics時，會在右邊看到策略建議。
第一個策略顯示為綠色，表示證明已成功完成。
接下來三個建議都是藍色，這表示無法直接完成證明，但不會導致錯誤。
因而，它們很有可能是有效的中間證明步驟！
同時，剩餘子目標也顯示了出來。
而Tactic state欄位顯示No goal，是因為至少有一個策略建議可以被證明。
圖片
搜尋完整證明
此外，因為人類和機器都不能始終如一地產生正確的策略，因此在這個過程中必須回溯、探索不同的替代方案，這個過程就是證明搜尋。
當是上面所說的Suggest_tropics，僅能產生目前步驟的策略，不具備搜尋多策略證明的能力。
為此，團隊將其與基於規則的證明搜尋工具aesop結合起來，建立了一個基於LLM的證明搜尋工具。
Aesop會將最佳優先搜尋作為Lean的策略實施，並且允許使用者配置搜尋樹的擴展方式。
圖片
搜尋樹是由作為節點的目標組成。
起初，它只有原始目標作為根節點。在每一步中，aesop都會選擇最有希望的未擴展節點，透過應用程式策略對其擴展，將產生的節點新增為子節點。
圖片
而當aesop找到一條從根源到可輕鬆解決的目標的路徑，就證明搜尋成功了！
因此，aesop的效能關鍵取決於使用者是否配置了有效的規則集。
這就可以看出，aesop缺乏彈性。因此，Search_proof透過在每個步驟中由suggest_tropics產生的目標相關策略，來增強aesop的規則集，讓它變得更加靈活。
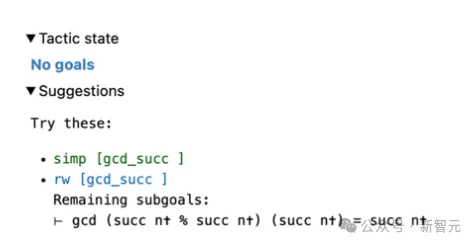
對於圖3中的原始目標，使用者只需輸入search_prrof，找到可以解決目標的完整證明，就顯示在了資訊視圖中（圖5右）。
可以看到，由於發現了成功的證據，所以剩餘的Tactic state是No goals。
圖片
選擇註解好的前提
此外，定理證明中另一個具有挑戰性的重要任務是，找到減少或完成證明的相關前提。
除了原始碼庫和標準函式庫中有大量前提，Lean還有一個大型數學函式庫（Mathlib）。
然而，從所有函式庫中搜尋候選前提，極為困難且耗時耗力。
所以許多人試圖，能在Lean，或其他的證明助手中得到輔助，或自動完成這一過程。
圖片
在Lean中，最先進的前提選擇方法是，直接在Lean中實現的基於隨機森林（ random forest）的框架。
然而，前提選擇任務非常適合檢索增強型LLM，即在大模型訓練期間訓練檢索矩陣（前提嵌入），以估計證明目標與候選前提之間的相關性。
給定推理時的證明目標，首先將目標編碼成一個向量，然後在前提嵌入和目標向量之間執行矩陣向量乘法。
然後，為了選擇前k個前提（其中k可以是超參數，決定使用者想要回傳多少前提），此時只要回傳得分最高的k個前提。
而要在Lean中執行推理任務，除了Lean Copilot提供的快速推理外，還需要一個高效的矩陣乘法庫和一個C 的numpy矩陣閱讀器。
研究人員採用了來自CTranslate2的矩陣乘法函數，和來自Libnpy的C 快速numpy檔案讀取器。
他們又透過FFI機制，將這些數字連結到Lean。
因此，前提選擇的策略可以非常有效率地運行，因為前提嵌入可以預先計算，所有後續操作都可以使用上文介紹的函式庫在C 中快速完成。
在獲得回傳的前提後，研究者進一步以有用的信息對其進行註解。
這裡將所有前提分為兩類：可直接在當前環境中使用的前提（範圍內前提）和不可直接在當前環境中使用的前提（範圍外前提）。
這取決於是否導入了所需的軟體包。
如果已經導入了前提所需的套件，則可以輕鬆使用該前提。如下圖6顯示了附註解的範圍內前提。
圖7所示是註解的範圍外前提。
下面舉個使用「前提選擇」的例子，對於圖3中的定理add_abc，可以直接在證明中輸入select_premises（圖8左）。
然後，相關前提的列表，就會出現在資訊視圖中（圖8右）。
對於這個簡單的定理，可以清楚地看到所選的前提確實相關，因為它們都與自然數和加法規則有關。
在這種情況下，所選的4個前提都在目前範圍內，這表示它們的模組已經導入。
如上，便是研究人員透過Lean Copilot建構的三個實用的證明自動化工具，用於策略建議、搜尋證明和前提選擇。
81.2%的證明步驟，全都自動化了
透過Lean Copilot框架，研究人員憑經驗提出了假設－在Lean互動定理證明（ITP）中進行人機協作是有益的。
由於Lean中的定理證明過程，主要以策略證明為主。
因此，在具體實驗中，作者主要評估了用於「策略建議」，以及「證明搜尋」的證明自動化工具。
總而言之，aesop是當前是一種用於證明搜索，最先進的基於規則的證明自動化工具。
研究人員在兩種情況下，驗證了基於LLM的搜尋證明與aesop相比的有效性：
（1）自主證明定理（LLM獨立完成）
（2）協助人類進行定理證明（人類與AI協作）
此外，研究者還將搜尋證明與策略建議進行了比較，以證明除了單一策略建議之外，搜尋證明體現的優勢。
研究Lean Copilot如何有效地幫助人類進行ITP的過程，類似於人類在軟體程式設計中使用Copilot的範式。
也就是說，當我們面對一個目標時，首先會呼叫Copilot，看其是否可以直接解決問題。
如果不能，我們會進一步簡化目標，然後再嘗試Copilot。然後，一直重複上述過程，直至Copilot成功解決剩餘目標。
而研究人員是透過這樣的迭代協作範例中，去查看每個證明自動化工具可以自動化多少人力。
具體結果，如下表1顯示。
證明搜尋（search_proof）可以自動證明64%的定理（50個中的32個），明顯高於aesop和策略建議（suggest_tropics）。
當用於輔助人類時，證明搜尋只需要平均1.02個手動輸入策略，這也比aesop（3.62）和策略建議（2.72）更好。
圖片
最後，對於每個測試的定理，作者計算了三個工具中每一個可以自動化的證明步驟的百分比。
結果發現，證明搜尋可以自動完成定理中約81.2%的證明步驟，明顯高於策略建議（48.6%）和aesop（35.2%）。
總之，證明搜尋的效能比策略建議，高出1.67倍，比基於規則的基線aesop高2.31倍。
透過Copilot在Lean中進行本地LLM推理
Lean Copilot中的tactic建議、證明搜尋和前提選擇，這三個任務本質上可能看起來不同，但對於使用者體驗的要求是相似的。
它們都需要足夠快速地產生回應，具有適中的運算需求，同時在Lean中運行。
使用者之所以有這些要求，是因為Lean本身在大多數情況下都能非常快速地提供環境回饋（例如剩餘目標，錯誤訊息，類型資訊等）。
這種快速，跟證明定理的本質是一致的－它需要連貫的推理。
如果Lean Copilot需要使用者等待很長一段時間，那麼人類和AI之間的協作就很難發揮作用。
同樣，我們也非常希望滿足低運算的需求。因為Lean中的定理證明本身不需要GPU，可以在使用者本地的筆記型電腦上運作。
因此，能夠在大多數硬體（包括沒有GPU的筆記型電腦）上高效運行，對於Lean的用戶就非常重要。
因為使用者在編寫證明時，可能無法存取支援CUDA的GPU。
因為需要滿足快速推理和低運算需求，而且所有流行的高效深度學習框架都是在Python中，團隊想到的一個自然的解決方案，就是在Python中託管模型(本地或遠端)，然後從Lean向模型發出請求。
然而，這種方法會受到進程間通訊的開銷的影響，並且它需要使用者執行額外的設定步驟，並不適合Lean的傳統工作流程。
為了克服這些問題，Lean Copilot透過外部功能介面(FFI)在Lean中本地運行LLM。
FFI是一種機制，可以用一種語言寫的程式呼叫另一種語言的子程式。
Lean部分用c 實現，可以與c 高效互通。
程式設計師可以在Lean中宣告一個函數，但在c 中實作函數體。實作會被編譯到一個共享庫中，並動態連結到Lean。
預設情況下，我們採用的是LeanDojo預訓練的repver模型。它基於一個編碼器-解碼器轉換器，BVT5，它將輸入字串映射到輸出字串。
Lean Copilot透過將模型包裝成一個對字串操作的c 函數，使其在Lean中可運行，該函數可以透過FFI在精益中呼叫。
圖片
華人作者立大功
最新論文中的三人團隊，也是23年6月開源平台LeanDojo其中的作者。
圖片
論文網址：https://arxiv.org/pdf/2306.15626.pdf
#Peiyang Song（宋沛洋）
圖片
宋沛洋是加州大學聖塔芭芭拉分校創意研究學院（CCS）的電腦科學榮譽本科生，導師是Richert Wang和Phill Conrad 。
同時，他也是加州理工學院計算與數學科學系（CMS）的SURF研究員，由Anima Anandkumar教授和Kaiyu Yang博士共同指導。
圖片
另外，他也是UC伯克利建築實驗室的研究員，與Tim Sherwood和Dr. Jeremy Lau（Google ）一起合作。
他的研究興趣是機器學習（ML），涉及自然語言處理（NLP）和電腦視覺（CV）等應用領域，以及系統和程式語言（PL）等基礎理論。
宋沛洋最近的研究主要有兩個方向。
一是神經符號推理和人工智慧數學（AI4Math），將大模型與互動式定理證明器（ITPs）相結。
另一個是基於時序邏輯的高能效機器學習。
Kaiyu Yang（楊凱峪）
圖片
楊凱峪是加州理工學院計算數學科學（CMS）系的博士後研究員，指導教授是Anima Anandkumar。
他曾在普林斯頓大學獲得了博士學位，導師是Jia Deng，也曾與Olga Russakovsky、陳丹琦一起工作。
他的研究重點是神經符號人工智慧，旨在使機器學習能夠進行符號推理，希望透過兩個方向實現：
（1）將機器學習應用於符號推理任務，如形式邏輯或自然語言中的數學推理和定理證明；
（2）將符號組件引入機器學習模型，使其更具可解釋性、可驗證性和數據高效。
目前，他正在研究能夠理解和推理數學的人工智慧。數學推理是人類智慧的一個重要里程碑，它有可能改變科學和工程中的許多重要問題，例如解決偏微分方程和公式驗證。
Anima Anandkumar
Anima Anandkumar現在是加州理工學院計算和數學科學教授。
圖片
她的研究興趣主要集中在大規模機器學習、非凸優化和高維度統計等領域。
特別是，她一直在帶頭開發和分析機器學習的張量演算法。
張量分解方法具有極高的平行性和可擴展性，可應用於大量資料。它可以保證收斂到最優解，並對許多機率模型（例如Markov模型）輸出一致的估計結果。
更廣泛地說，Anandkumar教授一直在研究加速非凸優化的高效技術。
參考資料：
https://www.php.cn/link/1dd5a4016c624ef51f0542d4ae60e281
#https://www.php.cn/link/ed798eec75807df6e79b0be391f720e4
#https://www.php.cn/link /a652e914c736dfaf8a6667ae6936f0d6
