如果是一个非常大的N <10000000 那么计算出来的N!也是非常大的,现在只需要知道最高位的数字。
通过斯特林公式可以计算。
特林斯公式: (公式1)
(公式1)
如下是算法:
result = 0.5* log(2*PI*(double)n)/log(10.0) + (double)n* log((double)n/E)/log(10.0);
result -= (int)result;
first_number = exp(result * log(10.0));
以上算法代码计算通过公式表示: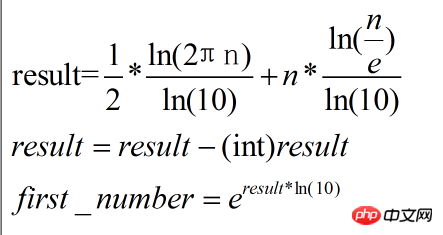 (公式2)
(公式2)
目前已知通过如下计算可以得到最高位: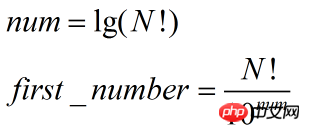 (公式3)
(公式3)
剩下的就是求N!,虽然N!可以通过特林斯计算,但是计算结果非常大。计算机直接计算会溢出结果,如下执行结果: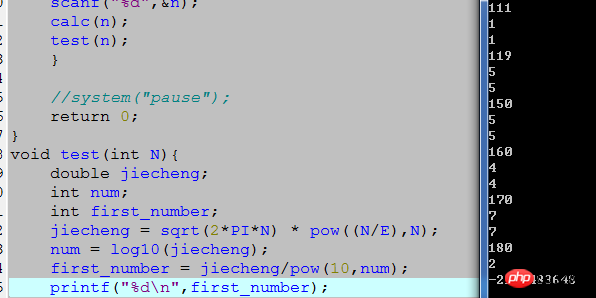
可以看出当执行到180的时候结果都已经溢出。
原因应该是在计算N! 的时候结果直接存储在计算机导致空间不足。
我所不明白的是为什么(公式2)的算法就可以直接计算出结果不溢出,且正确(当然数字过小的话也会有错误,比如0,1,2,3,7,8结果将不正确)。
最後是透過以10為底的對數log10(xxx)來求其最高位,這個你理解吧?他上面就是透過對數轉換把求以10為底的對數轉為以e為底的對數 aka: ln(yyy)
首先,鬍鬚佬頭,已經說的很明白了,原理就是他所說的那個,把原來用lg去求的問題,轉換為了ln去求。
我還是幫你貼張tu吧:(喜歡數學的都是好樣的)
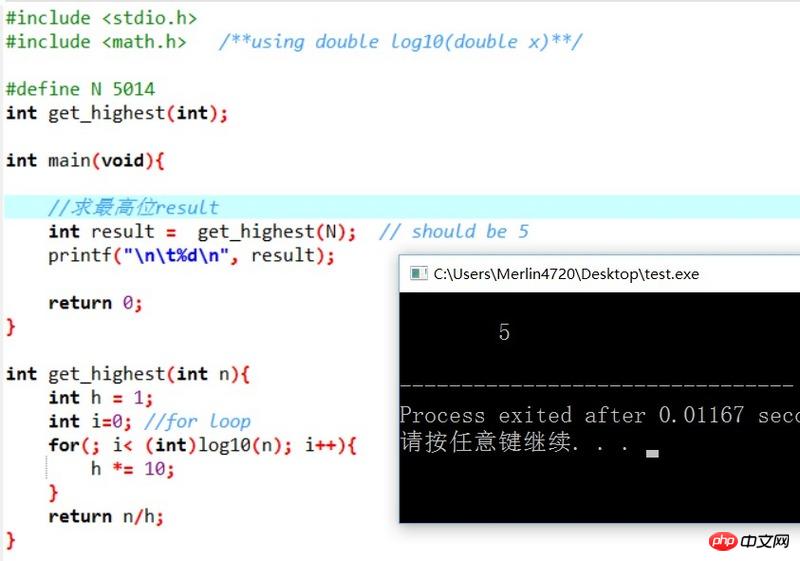
看到啦,其實上面已經驗證過了,如果要求5014的最高位,那麼可以寫成:
最高位= 5014 / (取整數)1g(5014); (注意類別C語言裡面,除法,會進行整數截斷)
ok,再說正事兒,你那個特林斯公式,假設拿到的階乘的近似值為X (一大串不管了,簡單點兒叫X),
如果想拿到這個數的最高位h,那麼有如下計算:
h = X / (int)lgX;
此時,透過特林斯公式,X 已求得,
計算一下「lgX的整數部分」就可以了。
先籠統的算(先不求整部和小數部分,直接算lgX)
lgX = lnX / ln10 (就是你上面把特林斯公式帶進去求值的那個式子,哦,你的圖還算錯了)
得到lgX= result (我化簡過了,不信你把那個特林斯公式化簡)
到這裡,就明白了,拿到result的整數部分,就能救出lgX的整數部分了,也就能求出最高位h.
而不是你說的「拿到小數部分」。
最後,根據你提供的特林斯公式,得到階乘factorial的值為:
X 約等於e^(ln10 * result的整數部分); (你可以自己從特林斯的公式變形到這一步看看)
似乎也不是你所說的
first_number = exp(result * log(10.0));
再有問題,在討論?貼出你最終的結果?