有关线性代数的Matlab代码笔记(2)行空间、零空间
今天继续,尝试加入一些范例 依然是简单的内容: %%%%%%%%%%%%%%%%%%%%% 说明 %%%%%%%%%%%%%%%%%%% 行空间的基 :按行的角度来看待矩阵,更多介绍在代码说明里,简单的利用了昨天的代码。 %%%%%%%%%%%%%%%%%%%%% CODE %%%%%%%%%%%%%%%%%% function B = rowba
今天继续,尝试加入一些范例
依然是简单的内容:
%%%%%%%%%%%%%%%%%%%%%说明 %%%%%%%%%%%%%%%%%%%
行空间的基:按行的角度来看待矩阵,更多介绍在代码说明里,简单的利用了昨天的代码。
%%%%%%%%%%%%%%%%%%%%%CODE %%%%%%%%%%%%%%%%%%
function B = rowbasis(A)
% rowbasis 行空间的基
%
% B = rowbasis(A) 返回A的行空间的一组基
% 以B的列表示
% A的行空间相当于A的转置的列空间
% rowbasis 找出A'中线性无关的
% 前r列,r代表A的秩
%
B = colbasis(A');
%%%%%%%%%%%%%%%%%%%%%范例 %%%%%%%%%%%%%%%%%%
>> A=[1,1,1;1,3,2;2,3,4]
A =
1 1 1
1 3 2
2 3 4
>> rowbasis(A)
ans =
1 1 2
1 3 3
1 2 4
%%%%%%%%%%%%%%%%%%%%%说明 %%%%%%%%%%%%%%%%%%%
零空间的基:这个零空间的代码值得好好看看,体现了线性代数里关于列意义的基本思想。
直接看去你可能会不知道这些代码在干什么。因为一个简单的语句可能包含了很多操作。
我自己不太明白的时候是喜欢举个例子,把代码一句一句执行来看看的。这里要注意的是
零空间里的列指示了矩阵里构成零向量的列的线性组合。而代码里用到了很多构成矩阵的办法。
%%%%%%%%%%%%%%%%%%%%%CODE %%%%%%%%%%%%%%%%%%
function N = nulbasis(A)
% nulbasis 零空间的基.
%
% N = nulbasis(A) 在N的列中返回A的零空间的一组基
% 包含了Ax=0的n-r个特殊解
% freecol是自由列.
%
% Example:
%
% >> A = [1 2 0 3;
% [0 0 1 4];
%
% >> N = nulbasis(A)
%
% N = [-2 -3]
% [ 1 0]
% [ 0 -4]
% [ 0 1]
%
[R, pivcol] = rref(A, sqrt(eps));%精度sqrt(eps)=1.4901e-008
[m, n] = size(A);
r = length(pivcol);
freecol = 1:n;
freecol(pivcol) = [];%主元所在列
N = zeros(n, n-r);
N(freecol, : ) = eye(n-r);%由自由列序号给零空间的行按单位矩阵赋值
N(pivcol, : ) = -R(1:r, freecol);%主元所在列赋行简化阶梯矩阵对应值相反数
%这样组合能得到零向量
%这个方法接近我们手动求零空间的算法

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 小红书笔记怎么删除
Mar 21, 2024 pm 08:12 PM
小红书笔记怎么删除
Mar 21, 2024 pm 08:12 PM
小红书笔记怎么删除?在小红书APP中是可以编辑笔记的,多数的用户不知道小红书笔记如何的删除,接下来就是小编为用户带来的小红书笔记删除方法图文教程,感兴趣的用户快来一起看看吧!小红书使用教程小红书笔记怎么删除1、首先打开小红书APP进入到主页面,选择右下角【我】进入到专区;2、之后在我的专区,点击下图所示的笔记页面,选择要删除的笔记;3、进入到笔记页面,右上角【三个点】;4、最后下方会展开功能栏,点击【删除】即可完成。
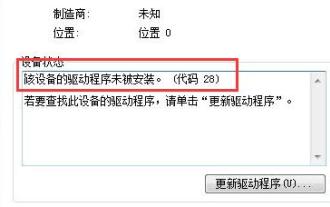 解决win7驱动程序代码28的方法
Dec 30, 2023 pm 11:55 PM
解决win7驱动程序代码28的方法
Dec 30, 2023 pm 11:55 PM
有的用户在安装设备的时候遇到了错误,提示错误代码28,其实这主要是由于驱动程序的原因,我们只要解决win7驱动程序代码28的问题就可以了,下面就一起来看一下应该怎么来操作吧。win7驱动程序代码28怎么办:首先,我们需要点击屏幕左下角的开始菜单。接着,在弹出的菜单中找到并点击“控制面板”选项。这个选项通常位于菜单的底部或者附近。点击后,系统会自动打开控制面板界面。在控制面板中,我们可以进行各种系统设置和管理操作。这是怀旧大扫除关卡中的第一步,希望对大家有所帮助。然后,我们需要继续操作,进入系统和
 蓝屏代码0x0000001怎么办
Feb 23, 2024 am 08:09 AM
蓝屏代码0x0000001怎么办
Feb 23, 2024 am 08:09 AM
蓝屏代码0x0000001怎么办蓝屏错误是电脑系统或硬件出现问题时的一种警告机制,代码0x0000001通常表示出现了硬件或驱动程序故障。当用户在使用电脑时突然遇到蓝屏错误,可能会感到惊慌和无措。幸运的是,大多数蓝屏错误都可以通过一些简单的步骤进行排除和处理。本文将为读者介绍一些解决蓝屏错误代码0x0000001的方法。首先,当遇到蓝屏错误时,我们可以尝试重
 小红书发布过的笔记不见了怎么办?它刚发的笔记搜不到的原因是什么?
Mar 21, 2024 pm 09:30 PM
小红书发布过的笔记不见了怎么办?它刚发的笔记搜不到的原因是什么?
Mar 21, 2024 pm 09:30 PM
作为一名小红书的用户,我们都曾遇到过发布过的笔记突然不见了的情况,这无疑让人感到困惑和担忧。在这种情况下,我们该怎么办呢?本文将围绕“小红书发布过的笔记不见了怎么办”这一主题,为你详细解答。一、小红书发布过的笔记不见了怎么办?首先,不要惊慌。如果你发现笔记不见了,保持冷静是关键,不要慌张。这可能是由于平台系统故障或操作失误引起的。检查发布记录很简单。只需打开小红书App,点击“我”→“发布”→“所有发布”,就可以查看自己的发布记录。在这里,你可以轻松找到之前发布的笔记。3.重新发布。如果找到了之
 scilab和matlab的区别
Dec 11, 2023 am 11:13 AM
scilab和matlab的区别
Dec 11, 2023 am 11:13 AM
scilab和matlab的区别:1、注释符号;2、预设变量的表示;3、操作符的用法;4、矩阵的定义与调用;5、程序的编辑与执行;6、数据类型;7、函数库;8、图形界面;9、社区支持与生态系统;10、跨平台兼容性;11、价格。详细介绍:1、注释符号,在Scilab中,注释是用“//”引导,而在Matlab中,注释是用“%”引导;2、预设变量的表示,在Scilab中等等。
 小红书怎么在笔记中添加商品链接 小红书在笔记中添加商品链接教程
Mar 12, 2024 am 10:40 AM
小红书怎么在笔记中添加商品链接 小红书在笔记中添加商品链接教程
Mar 12, 2024 am 10:40 AM
小红书怎么在笔记中添加商品链接?在小红书这款app中用户不仅可以浏览各种内容还可以进行购物,所以这款app中关于购物推荐、好物分享的内容是非常多的,如果小伙伴在这款app也是一个达人的话,也可以分享一些购物经验,找到商家进行合作,在笔记中添加连接之类的,很多人都愿意使用这款app购物,因为不仅方便,而且有很多达人会进行一些推荐,可以一边浏览有趣内容,一边看看有没有适合自己的衣服商品。一起看看如何在笔记中添加商品链接吧!小红书笔记添加商品链接方法 在手机桌面上打开app。 在app首页点击
 电脑频繁蓝屏而且每次代码不一样
Jan 06, 2024 pm 10:53 PM
电脑频繁蓝屏而且每次代码不一样
Jan 06, 2024 pm 10:53 PM
win10系统是一款非常优秀的高智能系统强大的智能可以为用户们带来最好的使用体验,一般正常的情况下用户们的win10系统电脑都不会出现任何的问题!但是在优秀的电脑也难免会出现各种故障最近一直有小伙伴们反应自己的win10系统遇到了频繁蓝屏的问题!今天小编就为大家带来了win10电脑频繁蓝屏不同代码的解决办法让我们一起来看一看吧。电脑频繁蓝屏而且每次代码不一样的解决办法:造成各种故障代码的原因以及解决建议1、0×000000116故障原因:应该是显卡驱动不兼容。解决建议:建议更换厂商原带驱动。2、
 解决代码0xc000007b错误
Feb 18, 2024 pm 07:34 PM
解决代码0xc000007b错误
Feb 18, 2024 pm 07:34 PM
终止代码0xc000007b在使用电脑时,有时会遇到各种各样的问题和错误代码。其中,终止代码最为令人困扰,尤其是终止代码0xc000007b。这个代码表示某个应用程序无法正常启动,给用户带来了不便。首先,我们来了解一下终止代码0xc000007b的含义。这个代码是Windows操作系统的错误代码,通常发生在32位应用程序尝试在64位操作系统上运行时。它表示应






