php 二叉树遍历算法与例子
二叉树算法在小编大学时学数据结构时会学到的一个算法了,这个可以在搜索与排序中提高50%的搜索性能了,下面我们来看一些关于php 二叉树遍历算法与例子吧。
二叉树遍历,是值从根节点出发,按照某种次序依次访问二叉树中的所有节点,使得每个节点被访问一次且仅被访问依

图是百度搜的。。。谢谢提供图的英雄。。
前序遍历二叉树:如果二叉树为空则返回,若二叉树非空,则先遍历左树,再遍历右树,遍历顺序为ABCDEGF。
中序遍历二叉树:如果二叉树为空则返回,若二叉树非空,则从根节点开始,中序遍历根节点的左子树,然后是访问根节点,最后中序遍历右子树,遍历顺序为CBEGDFA。
后序遍历二叉树:如果二叉树为空则返回,若二叉树非空,则从左到右先叶子后节点的访问遍历访问左右子树,最后是访问根节点。访问顺序为CGEFDBA。
层序遍历二叉树:如果二叉树为空则返回,若二叉树非空,则从树的第一层,也就是根节点开始访问,从上而下逐层遍历,在同一层中,按照从左到右的顺序对节点逐个访问。访问顺序为ABCDEFG。
现在,我们用PHP代码,来遍历二叉树结构。二叉树是放一个大数组,每一个节点都有三个字段,data表示这个节点的值,lChild表示这个节点的左边子节点,rChild表示这个节点的右边子节点。二叉树的结构我们用上面那张图。
二叉树结构代码如下:
//二叉树
$arr = array(
'data' => 'A',
'lChild' => array(
'data' => 'B',
'lChild' => array(
'data' => 'C',
'lChild' => array(),
'rChild' => array(),
),
'rChild' => array(
'data' => 'D',
'lChild' => array(
'data' => 'E',
'lChild' => array(),
'rChild' => array(
'data' => 'G',
'lChild' => array(),
'rChild' => array(),
),
),
'rChild' => array(
'data' => 'F',
'lChild' => array(),
'rChild' => array(),
),
),
),
'rChild' => array(),
);
遍历算法一:前序遍历二叉树
//前序遍历二叉树算法
echo '前序遍历二叉树算法:';
PreOrderTraverse($arr);
echo '
';
function PreOrderTraverse($node){
if(empty($node)){
return;
}
//输出值
print_r($node['data']);
//左节点
PreOrderTraverse($node['lChild']);
//右节点
PreOrderTraverse($node['rChild']);
}
遍历算法二:中序遍历二叉树
//中序遍历二叉树算法
echo '中序遍历二叉树算法:';
inOrderTraverse($arr);
echo '
';
function inOrderTraverse($node){
if(empty($node)){
return;
}
//左节点
inOrderTraverse($node['lChild']);
//输出值
print_r($node['data']);
//右节点
inOrderTraverse($node['rChild']);
}
遍历算法三:后序遍历二叉树
//后序遍历二叉树算法
echo '后序遍历二叉树算法:';
postOrderTraverse($arr);
echo '
';
function postOrderTraverse($node){
if(empty($node)){
return;
}
//左节点
postOrderTraverse($node['lChild']);
//右节点
postOrderTraverse($node['rChild']);
//输出值
print_r($node['data']);
}
例子
/**
*二叉树的创建及基本操作
*
*1.构造方法,初始化建立二叉树
*2.按先序遍历方式建立二叉树
*3.按先序遍历二叉树
*4.先序遍历的非递归算法
*5.中序遍历二叉树
*6.中序遍历的非递归算法
*7.后序遍历二叉树
*8.后序遍历非递归算法
*9.层次遍历二叉树
*10.求二叉树叶子结点的个数
*11.求二叉树的深度
*12.判断二叉树是否为空树
*13.置空二叉树
*
*@author xudianyang
*@version $Id:BinaryTree.class.php,v 1.0 2011/02/13 13:33:00 uw Exp
*@copyright ©2011,xudianyang
*/
header('content-type:text/html;charset=gb2312');
//在PHP数据结构之五 栈的PHP的实现和栈的基本操作 可以找到该类
include_once("./StackLinked.class.php");
//在 PHP数据结构之七 队列的链式存储和队列的基本操作 可以找到该类
include_once('./QueueLinked.class.php');
class BTNode{
//左子树“指针”
public $mLchild=null;
//右子树“指针”
public $mRchild=null;
//结点数据域
public $mData=null; //左标志域,为1时表示mLchild“指向”结点左孩子,为2表示“指向”结点直接前驱
public $intLeftTag=null;
//右标志域,为1时表示mRchild“指向”结点右孩子,为2表示“指向”结点直接后继
public $intRightTag=null;
}
class BinaryTree{
//根结点
public $mRoot;
//根据先序遍历录入的二叉树数据
public $mPBTdata=null;
/**
*构造方法,初始化建立二叉树
*
*@param array $btdata 根据先序遍历录入的二叉树的数据,一维数组,每一个元素代表二叉树一个结点值,扩充结点值为''[长度为0的字符串]
*@return void
*/
public function __construct($btdata=array()){
$this->mPBTdata=$btdata;
$this->mRoot=null;
$this->getPreorderTraversalCreate($this->mRoot);
}
/**
*按先序遍历方式建立二叉树
*
*@param BTNode 二叉树结点,按引用方式传递
*@return void
*/
public function getPreorderTraversalCreate(&$btnode){
$elem=array_shift($this->mPBTdata);
if($elem === ''){
$btnode=null;
}else if($elem === null){
return;
}else{
$btnode=new BTNode();
$btnode->mData=$elem;
$this->getPreorderTraversalCreate($btnode->mLchild);
$this->getPreorderTraversalCreate($btnode->mRchild);
}
}
/**
*判断二叉树是否为空
*
*@return boolean 如果二叉树不空返回true,否则返回false
**/
public function getIsEmpty(){
if($this->mRoot instanceof BTNode){
return false;
}else{
return true;
}
}
/**
*将二叉树置空
*
*@return void
*/
public function setBinaryTreeNull(){
$this->mRoot=null;
}
/**
*按先序遍历二叉树
*
*@param BTNode $rootnode 遍历过程中的根结点
*@param array $btarr 接收值的数组变量,按引用方式传递
*@return void
*/
public function getPreorderTraversal($rootnode,&$btarr){
if($rootnode!=null){
$btarr[]=$rootnode->mData;
$this->getPreorderTraversal($rootnode->mLchild,$btarr);
$this->getPreorderTraversal($rootnode->mRchild,$btarr);
}
}
/**
*先序遍历的非递归算法
*
*@param BTNode $objRootNode 二叉树根节点
*@param array $arrBTdata 接收值的数组变量,按引用方式传递
*@return void
*/
public function getPreorderTraversalNoRecursion($objRootNode,&$arrBTdata){
if($objRootNode instanceof BTNode){
$objNode=$objRootNode;
$objStack=new StackLinked();
do{
$arrBTdata[]=$objNode->mData;
$objRNode=$objNode->mRchild;
if($objRNode !=null){
$objStack->getPushStack($objRNode);
}
$objNode=$objNode->mLchild;
if($objNode==null){
$objStack->getPopStack($objNode);
}
}while($objNode!=null);
}else{
$arrBTdata=array();
}
}
/**
*中序遍历二叉树
*
*@param BTNode $objRootNode 过程中的根节点
*@param array $arrBTdata 接收值的数组变量,按引用方式传递
*@return void
*/
public function getInorderTraversal($objRootNode,&$arrBTdata){
if($objRootNode!=null){
$this->getInorderTraversal($objRootNode->mLchild,$arrBTdata);
$arrBTdata[]=$objRootNode->mData;
$this->getInorderTraversal($objRootNode->mRchild,$arrBTdata);
}
}
/**
*中序遍历的非递归算法
*
*@param BTNode $objRootNode 二叉树根结点
*@param array $arrBTdata 接收值的数组变量,按引用方式传递
*@return void
*/
public function getInorderTraversalNoRecursion($objRootNode,&$arrBTdata){
if($objRootNode instanceof BTNode){
$objNode=$objRootNode;
$objStack=new StackLinked();
//中序遍历左子树及访问根节点
do{
while($objNode!=null){
$objStack->getPushStack($objNode);
$objNode=$objNode->mLchild;
}
$objStack->getPopStack($objNode);
$arrBTdata[]=$objNode->mData;
$objNode=$objNode->mRchild;
}while(!$objStack->getIsEmpty());
//中序遍历右子树
do{
while($objNode!=null){
$objStack->getPushStack($objNode);
$objNode=$objNode->mLchild;
}
$objStack->getPopStack($objNode);
$arrBTdata[]=$objNode->mData;
$objNode=$objNode->mRchild;
}while(!$objStack->getIsEmpty());
}else{
$arrBTdata=array();
}
}
/**
*后序遍历二叉树
*
*@param BTNode $objRootNode 遍历过程中的根结点
*@param array $arrBTdata 接收值的数组变量,引用方式传递
*@return void
*/
public function getPostorderTraversal($objRootNode,&$arrBTdata){
if($objRootNode!=null){
$this->getPostorderTraversal($objRootNode->mLchild,$arrBTdata);
$this->getPostorderTraversal($objRootNode->mRchild,$arrBTdata);
$arrBTdata[]=$objRootNode->mData;
}
}
/**
*后序遍历非递归算法
*
BTNode $objRootNode 二叉树根节点
array $arrBTdata 接收值的数组变量,按引用方式传递
void
*/
public function getPostorderTraversalNoRecursion($objRootNode,&$arrBTdata){
if($objRootNode instanceof BTNode){
$objNode=$objRootNode;
$objStack=new StackLinked();
$objTagStack=new StackLinked();
$tag=1;
do{
while($objNode!=null){
$objStack->getPushStack($objNode);
$objTagStack->getPushStack(1);
$objNode=$objNode->mLchild;
}
$objTagStack->getPopStack($tag);
$objTagStack->getPushStack($tag);
if($tag == 1){
$objStack->getPopStack($objNode);
$objStack->getPushStack($objNode);
$objNode=$objNode->mRchild;
$objTagStack->getPopStack($tag);
$objTagStack->getPushStack(2);
}else{
$objStack->getPopStack($objNode);
$arrBTdata[]=$objNode->mData;
$objTagStack->getPopStack($tag);
$objNode=null;
}
}while(!$objStack->getIsEmpty());
}else{
$arrBTdata=array();
}
}
/**
*层次遍历二叉树
*
*@param BTNode $objRootNode二叉树根节点
*@param array $arrBTdata 接收值的数组变量,按引用方式传递
*@return void
*/
public function getLevelorderTraversal($objRootNode,&$arrBTdata){
if($objRootNode instanceof BTNode){
$objNode=$objRootNode;
$objQueue=new QueueLinked();
$objQueue->getInsertElem($objNode);
while(!$objQueue->getIsEmpty()){
$objQueue->getDeleteElem($objNode);
$arrBTdata[]=$objNode->mData;
if($objNode->mLchild != null){
$objQueue->getInsertElem($objNode->mLchild);
}
if($objNode->mRchild != null){
$objQueue->getInsertElem($objNode->mRchild);
}
}
}else{
$arrBTdata=array();
}
}
/**
*求二叉树叶子结点的个数
*
*@param BTNode $objRootNode 二叉树根节点
*@return int 参数传递错误返回-1
**/
public function getLeafNodeCount($objRootNode){
if($objRootNode instanceof BTNode){
$intLeafNodeCount=0;
$objNode=$objRootNode;
$objStack=new StackLinked();
do{
if($objNode->mLchild == null && $objNode->mRchild == null){
$intLeafNodeCount++;
}
$objRNode=$objNode->mRchild;
if($objRNode != null){
$objStack->getPushStack($objRNode);
}
$objNode=$objNode->mLchild;
if($objNode == null){
$objStack->getPopStack($objNode);
}
}while($objNode != null);
return $intLeafNodeCount;
}else{
return -1;
}
}
/**
*求二叉树的深度
*
*@param BTNode $objRootNode 二叉树根节点
*@return int 参数传递错误返回-1
*/
public function getBinaryTreeDepth($objRootNode){
if($objRootNode instanceof BTNode){
$objNode=$objRootNode;
$objQueue=new QueueLinked();
$intBinaryTreeDepth=0;
$objQueue->getInsertElem($objNode);
$objLevel=$objNode;
while(!$objQueue->getIsEmpty()){
$objQueue->getDeleteElem($objNode);
if($objNode->mLchild != null){
$objQueue->getInsertElem($objNode->mLchild);
}
if($objNode->mRchild != null){
$objQueue->getInsertElem($objNode->mRchild);
}
if($objLevel == $objNode){
$intBinaryTreeDepth++;
$objLevel=@$objQueue->mRear->mElem;
}
}
return $intBinaryTreeDepth;
}else{
return -1;
}
}
}
echo "
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
|
?>

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)
 解决方法:您的组织要求您更改 PIN 码
Oct 04, 2023 pm 05:45 PM
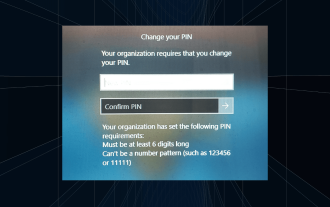
解决方法:您的组织要求您更改 PIN 码
Oct 04, 2023 pm 05:45 PM
“你的组织要求你更改PIN消息”将显示在登录屏幕上。当在使用基于组织的帐户设置的电脑上达到PIN过期限制时,就会发生这种情况,在该电脑上,他们可以控制个人设备。但是,如果您使用个人帐户设置了Windows,则理想情况下不应显示错误消息。虽然情况并非总是如此。大多数遇到错误的用户使用个人帐户报告。为什么我的组织要求我在Windows11上更改我的PIN?可能是您的帐户与组织相关联,您的主要方法应该是验证这一点。联系域管理员会有所帮助!此外,配置错误的本地策略设置或不正确的注册表项也可能导致错误。即
 Windows 11 上调整窗口边框设置的方法:更改颜色和大小
Sep 22, 2023 am 11:37 AM
Windows 11 上调整窗口边框设置的方法:更改颜色和大小
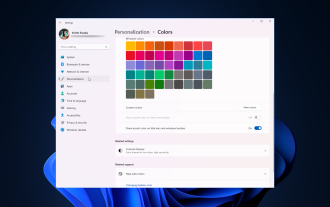
Sep 22, 2023 am 11:37 AM
Windows11将清新优雅的设计带到了最前沿;现代界面允许您个性化和更改最精细的细节,例如窗口边框。在本指南中,我们将讨论分步说明,以帮助您在Windows操作系统中创建反映您的风格的环境。如何更改窗口边框设置?按+打开“设置”应用。WindowsI转到个性化,然后单击颜色设置。颜色更改窗口边框设置窗口11“宽度=”643“高度=”500“>找到在标题栏和窗口边框上显示强调色选项,然后切换它旁边的开关。若要在“开始”菜单和任务栏上显示主题色,请打开“在开始”菜单和任务栏上显示主题
 如何在 Windows 11 上更改标题栏颜色?
Sep 14, 2023 pm 03:33 PM
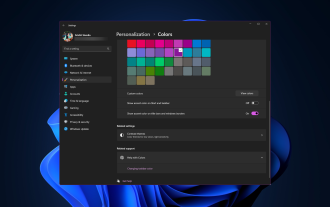
如何在 Windows 11 上更改标题栏颜色?
Sep 14, 2023 pm 03:33 PM
默认情况下,Windows11上的标题栏颜色取决于您选择的深色/浅色主题。但是,您可以将其更改为所需的任何颜色。在本指南中,我们将讨论三种方法的分步说明,以更改它并个性化您的桌面体验,使其具有视觉吸引力。是否可以更改活动和非活动窗口的标题栏颜色?是的,您可以使用“设置”应用更改活动窗口的标题栏颜色,也可以使用注册表编辑器更改非活动窗口的标题栏颜色。若要了解这些步骤,请转到下一部分。如何在Windows11中更改标题栏的颜色?1.使用“设置”应用按+打开设置窗口。WindowsI前往“个性化”,然
 Windows 11 上启用或禁用任务栏缩略图预览的方法
Sep 15, 2023 pm 03:57 PM
Windows 11 上启用或禁用任务栏缩略图预览的方法
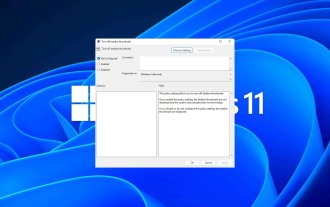
Sep 15, 2023 pm 03:57 PM
任务栏缩略图可能很有趣,但它们也可能分散注意力或烦人。考虑到您将鼠标悬停在该区域的频率,您可能无意中关闭了重要窗口几次。另一个缺点是它使用更多的系统资源,因此,如果您一直在寻找一种提高资源效率的方法,我们将向您展示如何禁用它。不过,如果您的硬件规格可以处理它并且您喜欢预览版,则可以启用它。如何在Windows11中启用任务栏缩略图预览?1.使用“设置”应用点击键并单击设置。Windows单击系统,然后选择关于。点击高级系统设置。导航到“高级”选项卡,然后选择“性能”下的“设置”。在“视觉效果”选
 OOBELANGUAGE错误Windows 11 / 10修复中出现问题的问题
Jul 16, 2023 pm 03:29 PM
OOBELANGUAGE错误Windows 11 / 10修复中出现问题的问题
Jul 16, 2023 pm 03:29 PM
您是否在Windows安装程序页面上看到“出现问题”以及“OOBELANGUAGE”语句?Windows的安装有时会因此类错误而停止。OOBE表示开箱即用的体验。正如错误提示所表示的那样,这是与OOBE语言选择相关的问题。没有什么可担心的,你可以通过OOBE屏幕本身的漂亮注册表编辑来解决这个问题。快速修复–1.单击OOBE应用底部的“重试”按钮。这将继续进行该过程,而不会再打嗝。2.使用电源按钮强制关闭系统。系统重新启动后,OOBE应继续。3.断开系统与互联网的连接。在脱机模式下完成OOBE的所
 Windows 11 上的显示缩放比例调整指南
Sep 19, 2023 pm 06:45 PM
Windows 11 上的显示缩放比例调整指南
Sep 19, 2023 pm 06:45 PM
在Windows11上的显示缩放方面,我们都有不同的偏好。有些人喜欢大图标,有些人喜欢小图标。但是,我们都同意拥有正确的缩放比例很重要。字体缩放不良或图像过度缩放可能是工作时真正的生产力杀手,因此您需要知道如何对其进行自定义以充分利用系统功能。自定义缩放的优点:对于难以阅读屏幕上的文本的人来说,这是一个有用的功能。它可以帮助您一次在屏幕上查看更多内容。您可以创建仅适用于某些监视器和应用程序的自定义扩展配置文件。可以帮助提高低端硬件的性能。它使您可以更好地控制屏幕上的内容。如何在Windows11
 10种在 Windows 11 上调整亮度的方法
Dec 18, 2023 pm 02:21 PM
10种在 Windows 11 上调整亮度的方法
Dec 18, 2023 pm 02:21 PM
屏幕亮度是使用现代计算设备不可或缺的一部分,尤其是当您长时间注视屏幕时。它可以帮助您减轻眼睛疲劳,提高易读性,并轻松有效地查看内容。但是,根据您的设置,有时很难管理亮度,尤其是在具有新UI更改的Windows11上。如果您在调整亮度时遇到问题,以下是在Windows11上管理亮度的所有方法。如何在Windows11上更改亮度[10种方式解释]单显示器用户可以使用以下方法在Windows11上调整亮度。这包括使用单个显示器的台式机系统以及笔记本电脑。让我们开始吧。方法1:使用操作中心操作中心是访问
 华为GT3 Pro和GT4的差异是什么?
Dec 29, 2023 pm 02:27 PM
华为GT3 Pro和GT4的差异是什么?
Dec 29, 2023 pm 02:27 PM
许多用户在选择智能手表的时候都会选择的华为的品牌,其中华为GT3pro和GT4都是非常热门的选择,不少用户都很好奇华为GT3pro和GT4有什么区别,下面就就给大家介绍一下二者。华为GT3pro和GT4有什么区别一、外观GT4:46mm和41mm,材质是玻璃表镜+不锈钢机身+高分纤维后壳。GT3pro:46.6mm和42.9mm,材质是蓝宝石玻璃表镜+钛金属机身/陶瓷机身+陶瓷后壳二、健康GT4:采用最新的华为Truseen5.5+算法,结果会更加的精准。GT3pro:多了ECG心电图和血管及安






