ICLR 2024 Spotlight | 无惧中间步骤,MUSTARD可生成高质量数学推理数据

AIxiv专栏是本站发布学术、技术内容的栏目。过去数年,本站AIxiv专栏接收报道了2000多篇内容,覆盖全球各大高校与企业的顶级实验室,有效促进了学术交流与传播。如果您有优秀的工作想要分享,欢迎投稿或者联系报道。投稿邮箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com。

论文题目:MUSTARD: Mastering Uniform Synthesis of Theorem and Proof Data 论文链接:https://openreview.net/forum?id=8xliOUg9EW 代码链接:https://github.com/Eleanor-H/MUSTARD 数据集链接:https://drive.google.com/file/d/1yIVAVqpkC2Op7LhisG6BJJ_-MavAMr1B/view 作者主页:https://eleanor-h.github.io/
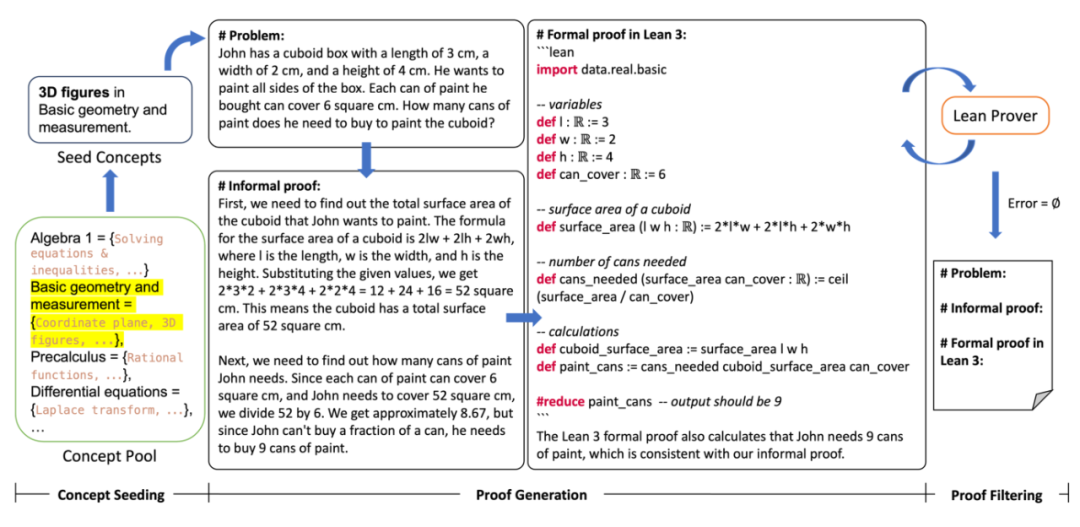

MUSTARDSAUCE-valid:经过了 Lean 形式化证明器验证的 5866 条数据; MUSTARDSAUCE-invalid:未能通过 Lean 形式化证明器验证的 5866 条数据; MUSTARDSAUCE-random:随机的 5866 条数据; MUSTARDSAUCE-tt:MUSTARD 生成的所有 28316 条数据。




赛道 1-1 (自动形式化):https://www.codabench.org/competitions/2436/ 赛道 1-2 (自动非形式化):https://www.codabench.org/competitions/2484/ 赛道 2 (自动定理生成和证明):https://www.codabench.org/competitions/2437/ 赛道 3 (代码辅助的运筹优化问题自动求解):https://www.codabench.org/competitions/2438/
以上是ICLR 2024 Spotlight | 无惧中间步骤,MUSTARD可生成高质量数学推理数据的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)
 DeepMind机器人打乒乓球,正手、反手溜到飞起,全胜人类初学者
Aug 09, 2024 pm 04:01 PM
DeepMind机器人打乒乓球,正手、反手溜到飞起,全胜人类初学者
Aug 09, 2024 pm 04:01 PM
但可能打不过公园里的老大爷?巴黎奥运会正在如火如荼地进行中,乒乓球项目备受关注。与此同时,机器人打乒乓球也取得了新突破。刚刚,DeepMind提出了第一个在竞技乒乓球比赛中达到人类业余选手水平的学习型机器人智能体。论文地址:https://arxiv.org/pdf/2408.03906DeepMind这个机器人打乒乓球什么水平呢?大概和人类业余选手不相上下:正手反手都会:对手采用多种打法,该机器人也能招架得住:接不同旋转的发球:不过,比赛激烈程度似乎不如公园老大爷对战。对机器人来说,乒乓球运动
 首配机械爪!元萝卜亮相2024世界机器人大会,发布首个走进家庭的国际象棋机器人
Aug 21, 2024 pm 07:33 PM
首配机械爪!元萝卜亮相2024世界机器人大会,发布首个走进家庭的国际象棋机器人
Aug 21, 2024 pm 07:33 PM
8月21日,2024世界机器人大会在北京隆重召开。商汤科技旗下家用机器人品牌“元萝卜SenseRobot”家族全系产品集体亮相,并最新发布元萝卜AI下棋机器人——国际象棋专业版(以下简称“元萝卜国象机器人”),成为全球首个走进家庭的国际象棋机器人。作为元萝卜的第三款下棋机器人产品,全新的国象机器人在AI和工程机械方面进行了大量专项技术升级和创新,首次在家用机器人上实现了通过机械爪拾取立体棋子,并进行人机对弈、人人对弈、记谱复盘等功能,
 Claude也变懒了!网友:学会给自己放假了
Sep 02, 2024 pm 01:56 PM
Claude也变懒了!网友:学会给自己放假了
Sep 02, 2024 pm 01:56 PM
开学将至,该收心的不止有即将开启新学期的同学,可能还有AI大模型。前段时间,Reddit上挤满了吐槽Claude越来越懒的网友。「它的水平下降了很多,经常停顿,甚至输出也变得很短。在发布的第一周,它可以一次性翻译整整4页文稿,现在连半页都输出不了了!」https://www.reddit.com/r/ClaudeAI/comments/1by8rw8/something_just_feels_wrong_with_claude_in_the/在一个名为「对Claude彻底失望了的帖子里」,满满地
 世界机器人大会上,这家承载「未来养老希望」的国产机器人被包围了
Aug 22, 2024 pm 10:35 PM
世界机器人大会上,这家承载「未来养老希望」的国产机器人被包围了
Aug 22, 2024 pm 10:35 PM
正在北京举行的世界机器人大会上,人形机器人的展示成为了现场绝对的焦点,在星尘智能的展台上,由于AI机器人助理S1在一个展区上演扬琴、武术、书法三台大戏,能文能武,吸引了大量专业观众和媒体的驻足。在带弹性的琴弦上的优雅演奏,让S1展现出速度、力度、精度兼具的精细操作和绝对掌控。央视新闻对「书法」背后的模仿学习和智能控制进行了专题报道,公司创始人来杰解释到,丝滑动作的背后,是硬件侧追求最好力控和最仿人身体指标(速度、负载等),而是在AI侧则采集人的真实动作数据,让机器人遇强则强,快速学习进化。而敏捷
 ACL 2024奖项公布:华科大破译甲骨文最佳论文之一、GloVe时间检验奖
Aug 15, 2024 pm 04:37 PM
ACL 2024奖项公布:华科大破译甲骨文最佳论文之一、GloVe时间检验奖
Aug 15, 2024 pm 04:37 PM
本届ACL大会,投稿者「收获满满」。为期六天的ACL2024正在泰国曼谷举办。ACL是计算语言学和自然语言处理领域的顶级国际会议,由国际计算语言学协会组织,每年举办一次。一直以来,ACL在NLP领域的学术影响力都位列第一,它也是CCF-A类推荐会议。今年的ACL大会已是第62届,接收了400余篇NLP领域的前沿工作。昨天下午,大会公布了最佳论文等奖项。此次,最佳论文奖7篇(两篇未公开)、最佳主题论文奖1篇、杰出论文奖35篇。大会还评出了资源论文奖(ResourceAward)3篇、社会影响力奖(
 李飞飞团队提出ReKep,让机器人具备空间智能,还能整合GPT-4o
Sep 03, 2024 pm 05:18 PM
李飞飞团队提出ReKep,让机器人具备空间智能,还能整合GPT-4o
Sep 03, 2024 pm 05:18 PM
视觉与机器人学习的深度融合。当两只机器手丝滑地互相合作叠衣服、倒茶、将鞋子打包时,加上最近老上头条的1X人形机器人NEO,你可能会产生一种感觉:我们似乎开始进入机器人时代了。事实上,这些丝滑动作正是先进机器人技术+精妙框架设计+多模态大模型的产物。我们知道,有用的机器人往往需要与环境进行复杂精妙的交互,而环境则可被表示成空间域和时间域上的约束。举个例子,如果要让机器人倒茶,那么机器人首先需要抓住茶壶手柄并使之保持直立,不泼洒出茶水,然后平稳移动,一直到让壶口与杯口对齐,之后以一定角度倾斜茶壶。这
 分布式人工智能盛会DAI 2024征稿:Agent Day,强化学习之父Richard Sutton将出席!颜水成、Sergey Levine以及DeepMind科学家将做主旨报告
Aug 22, 2024 pm 08:02 PM
分布式人工智能盛会DAI 2024征稿:Agent Day,强化学习之父Richard Sutton将出席!颜水成、Sergey Levine以及DeepMind科学家将做主旨报告
Aug 22, 2024 pm 08:02 PM
会议简介随着科技的飞速发展,人工智能已经成为了推动社会进步的重要力量。在这个时代,我们有幸见证并参与到分布式人工智能(DistributedArtificialIntelligence,DAI)的创新与应用中。分布式人工智能是人工智能领域的重要分支,这几年引起了越来越多的关注。基于大型语言模型(LLM)的智能体(Agent)异军突起,通过结合大模型的强大语言理解和生成能力,展现出了在自然语言交互、知识推理、任务规划等方面的巨大潜力。AIAgent正在接棒大语言模型,成为当前AI圈的热点话题。Au
 鸿蒙智行享界S9及全场景新品发布会,多款重磅新品齐发
Aug 08, 2024 am 07:02 AM
鸿蒙智行享界S9及全场景新品发布会,多款重磅新品齐发
Aug 08, 2024 am 07:02 AM
今天下午,鸿蒙智行正式迎来了新品牌与新车。 8月6日,华为举行鸿蒙智行享界S9及华为全场景新品发布会,带来了全景智慧旗舰轿车享界S9、问界新M7Pro和华为novaFlip、MatePadPro12.2英寸、全新MatePadAir、华为毕升激光打印机X1系列、FreeBuds6i、WATCHFIT3和智慧屏S5Pro等多款全场景智慧新品,从智慧出行、智慧办公到智能穿戴,华为全场景智慧生态持续构建,为消费者带来万物互联的智慧体验。鸿蒙智行:深度赋能,推动智能汽车产业升级华为联合中国汽车产业伙伴,为






