递归方法是一种调用自身的方法。许多数学函数是使用递归定义的。让我们从一个简单的例子开始。数字 n 的阶乘可以递归定义如下:
0! = 1;
嗯! = n × (n - 1)!; n> 0
如何找到给定 n 的 n!?查找 1! 很容易,因为您知道 0! 是 1,而 1! 是 1 × 0 !。假设你知道(n - 1)!,你可以通过使用n × (n - 1)!立即获得n!。因此,计算 n! 的问题就简化为计算 (n - 1)!。当计算 (n - 1)! 时,您可以递归地应用相同的想法,直到 n 减少到 0.
设 factorial(n) 为计算 n! 的方法。如果您使用 n = 0 调用该方法,它会立即返回结果。该方法知道如何解决最简单的情况,称为基本情况或停止条件。如果您使用 n > 调用该方法; 0,它将问题简化为计算 n - 1 阶乘的子问题。 子问题本质上与原始问题相同,但更简单或更小。由于子问题与原始问题具有相同的属性,因此您可以使用不同的参数调用该方法,这称为递归调用.
计算factorial(n)的递归算法可以简单描述如下:
如果(n == 0)
返回 1;
其他
返回 n * 阶乘(n - 1);
递归调用可能会导致更多的递归调用,因为该方法不断将子问题划分为新的子问题。对于要终止的递归方法,问题最终必须减少到停止情况,此时该方法将结果返回给其调用者。然后调用者执行计算并将结果返回给其自己的调用者。这个过程一直持续到结果被传回原始调用者为止。现在可以通过将 n 乘以阶乘(n - 1) 的结果来解决原来的问题。
下面的代码给出了一个完整的程序,提示用户输入一个非负整数并显示该数字的阶乘。

factorial 方法(第 17-22 行)本质上是将阶乘的递归数学定义直接转换为 Java 代码。对 factorial 的调用是递归的,因为它调用自身。传递给 factorial 的参数会递减,直到达到 0 的基本情况。
您将了解如何编写递归方法。递归在幕后如何工作?下图说明了递归调用的执行过程,从 n = 4.
开始
递归调用时栈空间的使用如下图所示。
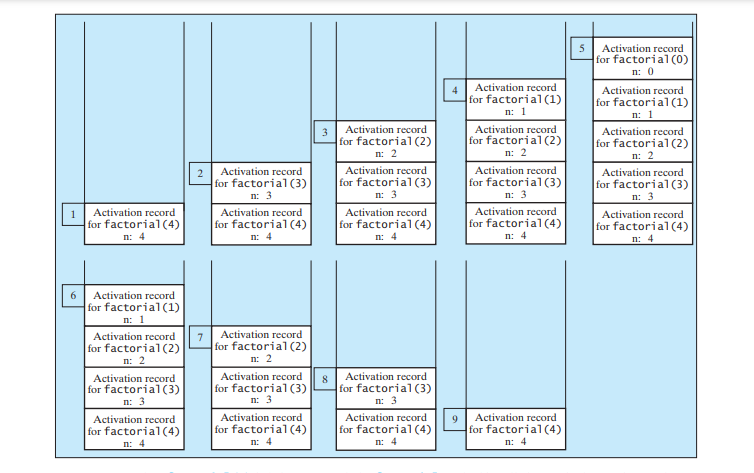
使用循环实现 factorial 方法更简单、更高效。然而,我们在这里使用递归阶乘方法来演示递归的概念。在本章后面,我们将介绍一些本质上是递归的问题,如果不使用递归就很难解决。
如果递归不能以允许问题最终收敛到基本情况的方式减少问题,或者未指定基本情况,则可能会发生无限递归。例如,假设您错误地将 factorial 方法编写如下:
公共静态长阶乘(int n) {
返回 n * 阶乘(n - 1);
}
该方法无限运行并导致 StackOverflowError.
本节讨论的示例显示了一个调用自身的递归方法。这称为直接递归。还可以创建间接递归。当方法 A 调用方法 B 时,会发生这种情况,方法 B 又调用方法 A。递归中甚至可以涉及更多方法。例如,方法 A 调用方法 B,方法 B 调用方法
C,方法 C 调用方法 A。以上是案例研究:计算阶乘的详细内容。更多信息请关注PHP中文网其他相关文章!




