逻辑回归，分类：监督机器学习-Python教程-PHP中文网

什么是分类？

定义和目的

分类是机器学习和数据科学中使用的一种监督学习技术，用于将数据分类为预定义的类或标签。它涉及训练一个模型，根据输入数据点的特征将其分配给几个离散类别之一。分类的主要目的是准确预测新的、未见过的数据点的类别。

主要目标：

预测：将新数据点分配给预定义的类之一。
估计：确定数据点属于特定类别的概率。
理解关系：识别哪些特征对于预测数据点的类别很重要。

分类类型

1。二元分类

描述：将数据分类为两个类别之一。
- 示例：垃圾邮件检测（垃圾邮件或非垃圾邮件）、疾病诊断（有病或无疾病）。
- 目的：区分两个不同的类。

2。多类分类

描述：将数据分类为三个或更多类别之一。
- 示例：手写数字识别（数字0-9）、花卉种类分类（多种）。
- 目的：处理需要预测两个以上类别的问题。

什么是线性分类器？

线性分类器是一类分类算法，它使用线性决策边界来分离特征空间中的不同类。他们通过线性方程组合输入特征来进行预测，通常表示特征和目标类标签之间的关系。线性分类器的主要目的是通过找到将特征空间划分为不同类的超平面来有效地对数据点进行分类。

逻辑回归

定义和目的

逻辑回归是一种用于机器学习和数据科学中二元分类任务的统计方法。它是线性分类器的一部分，与线性回归不同，它通过将数据拟合到逻辑曲线来预测事件发生的概率。

主要目标：

二元分类：预测二元结果（例如，是/否、真/假）。
概率估计：根据输入变量估计事件发生的概率。
决策边界：确定将数据分类为不同类别的阈值。

逻辑回归模型

1。 Logistic 函数（S 型函数）

描述：逻辑函数将任何实值输入转换为 0 到 1 之间的值，使其适合概率建模。
- 方程: σ(z) = 1 / (1 + e^(-z))
- 目的：将输入值映射到概率。

2。逻辑回归方程

描述：逻辑回归模型将逻辑函数应用于输入变量的线性组合。
- 方程：P(y=1|x) = σ(w0 + w1x1 + w2x2 + ... + wnxn)
- 目的：在给定输入变量x的情况下预测二元结果y=1的概率P(y=1|x)。

最大似然估计（MLE）

MLE 用于通过最大化观察给定模型的数据的可能性来估计逻辑回归模型的参数（系数）。

方程：最大化对数似然函数涉及找到最大化观察数据的概率的参数。

逻辑回归中的成本函数和损失最小化

成本函数

逻辑回归中的成本函数衡量预测概率与实际类别标签之间的差异。目标是最小化此函数以提高模型的预测准确性。

对数损失（二元交叉熵）:
对数损失函数常用于二元分类任务的逻辑回归。

对数损失 = -(1/n) * Σ [y * log(ŷ) + (1 - y) * log(1 - ŷ)]

地点：

y 是实际的类标签（0 或 1），
ŷ 是类标签的预测概率，
n 是数据点的数量。

对数损失会惩罚远离实际类别标签的预测，从而鼓励模型产生准确的概率。

损失最小化（优化）

逻辑回归中的

损失最小化涉及找到最小化成本函数值的模型参数值。此过程也称为优化。逻辑回归中损失最小化最常见的方法是梯度下降算法。

梯度下降

梯度下降是一种迭代优化算法，用于最小化逻辑回归中的成本函数。它沿着成本函数最速下降的方向调整模型参数。

梯度下降的步骤:

初始化参数：从模型参数的初始值开始（例如系数 w0、w1、...、wn）。
计算梯度：计算成本函数相对于每个参数的梯度。梯度是成本函数的偏导数。
更新参数：向渐变的相反方向调整参数。调整由学习率 (α) 控制，它决定了向最小值迈出的步长。
重复：迭代该过程，直到成本函数收敛到最小值（或达到预定义的迭代次数）。

参数更新规则:
对于每个参数 wj：
wj = wj - α * (∂/∂wj) 对数损失

地点：

α 是学习率，
(∂/∂wj) Log Loss 是对数损失关于 wj 的偏导数。

对数损失关于 wj 的偏导数可以计算为：
(∂/∂wj) 对数损失 = -(1/n) * Σ [ (yi - ŷi) * xij / (ŷi * (1 - ŷi)) ]

地点：

xij 是第 i 个数据点的第 j 个自变量的值，
ŷi 是第 i 个数据点的类标签的预测概率。

Logistic 回归（二元分类）示例

逻辑回归是一种用于二元分类任务的技术，对给定输入属于特定类别的概率进行建模。此示例演示了如何使用合成数据实现逻辑回归、评估模型的性能以及可视化决策边界。

Python 代码示例

1。导入库

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

登录后复制

此块导入数据操作、绘图和机器学习所需的库。

2。生成样本数据

np.random.seed(42)  # For reproducibility
X = np.random.randn(1000, 2)
y = (X[:, 0] + X[:, 1] > 0).astype(int)

登录后复制

该块生成具有两个特征的样本数据，其中根据特征之和是否大于零来定义目标变量 y，模拟二元分类场景。

3。分割数据集

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

登录后复制

此块将数据集拆分为训练集和测试集以进行模型评估。

4。创建并训练逻辑回归模型

model = LogisticRegression(random_state=42)
model.fit(X_train, y_train)

登录后复制

此块初始化逻辑回归模型并使用训练数据集对其进行训练。

5。做出预测

y_pred = model.predict(X_test)

登录后复制

此块使用经过训练的模型对测试集进行预测。

6。评估模型

accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
class_report = classification_report(y_test, y_pred)

print(f"Accuracy: {accuracy:.4f}")
print("\nConfusion Matrix:")
print(conf_matrix)
print("\nClassification Report:")
print(class_report)

登录后复制

输出：

Accuracy: 0.9950

Confusion Matrix:
[[ 92   0]
 [  1 107]]

Classification Report:
              precision    recall  f1-score   support

           0       0.99      1.00      0.99        92
           1       1.00      0.99      1.00       108

    accuracy                           0.99       200
   macro avg       0.99      1.00      0.99       200
weighted avg       1.00      0.99      1.00       200

登录后复制

此块计算并打印准确性、混淆矩阵和分类报告，提供对模型性能的深入了解。

7。可视化决策边界

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
                     np.arange(y_min, y_max, 0.1))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.figure(figsize=(10, 8))
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=0.8)
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.title("Logistic Regression Decision Boundary")
plt.show()

登录后复制

此块可视化由逻辑回归模型创建的决策边界，说明模型如何在特征空间中分离两个类。

输出：

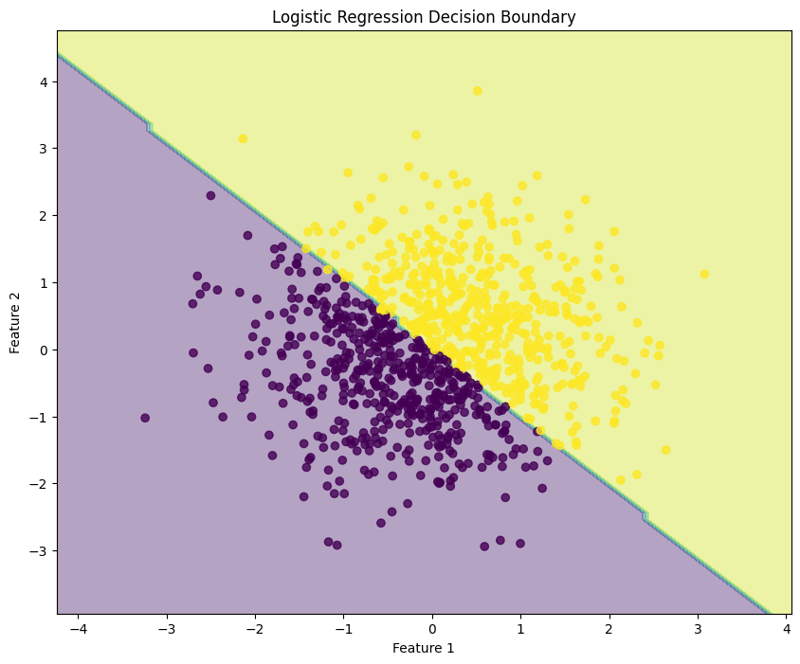
Logistic Regression Binary Classification

这种结构化方法演示了如何实现和评估逻辑回归，让人们清楚地了解其二元分类任务的功能。决策边界的可视化有助于解释模型的预测。

Logistic Regression (Multiclass Classification) Example

Logistic regression can also be applied to multiclass classification tasks. This example demonstrates how to implement logistic regression using synthetic data, evaluate the model's performance, and visualize the decision boundary for three classes.

Python Code Example

1. Import Libraries

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

登录后复制

This block imports the necessary libraries for data manipulation, plotting, and machine learning.

2. Generate Sample Data with 3 Classes

np.random.seed(42)  # For reproducibility
n_samples = 999  # Total number of samples
n_samples_per_class = 333  # Ensure this is exactly n_samples // 3

# Class 0: Top-left corner
X0 = np.random.randn(n_samples_per_class, 2) * 0.5 + [-2, 2]

# Class 1: Top-right corner
X1 = np.random.randn(n_samples_per_class, 2) * 0.5 + [2, 2]

# Class 2: Bottom center
X2 = np.random.randn(n_samples_per_class, 2) * 0.5 + [0, -2]

# Combine the data
X = np.vstack([X0, X1, X2])
y = np.hstack([np.zeros(n_samples_per_class), 
               np.ones(n_samples_per_class), 
               np.full(n_samples_per_class, 2)])

# Shuffle the dataset
shuffle_idx = np.random.permutation(n_samples)
X, y = X[shuffle_idx], y[shuffle_idx]

登录后复制

This block generates synthetic data for three classes located in different regions of the feature space.

3. Split the Dataset

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

登录后复制

This block splits the dataset into training and testing sets for model evaluation.

4. Create and Train the Logistic Regression Model

model = LogisticRegression(random_state=42)
model.fit(X_train, y_train)

登录后复制

This block initializes the logistic regression model and trains it using the training dataset.

5. Make Predictions

y_pred = model.predict(X_test)

登录后复制

This block uses the trained model to make predictions on the test set.

6. Evaluate the Model

accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
class_report = classification_report(y_test, y_pred)

print(f"Accuracy: {accuracy:.4f}")
print("\nConfusion Matrix:")
print(conf_matrix)
print("\nClassification Report:")
print(class_report)

登录后复制

Output:

Accuracy: 1.0000

Confusion Matrix:
[[54  0  0]
 [ 0 65  0]
 [ 0  0 81]]

Classification Report:
              precision    recall  f1-score   support

         0.0       1.00      1.00      1.00        54
         1.0       1.00      1.00      1.00        65
         2.0       1.00      1.00      1.00        81

    accuracy                           1.00       200
   macro avg       1.00      1.00      1.00       200
weighted avg       1.00      1.00      1.00       200

登录后复制

This block calculates and prints the accuracy, confusion matrix, and classification report, providing insights into the model's performance.

7. Visualize the Decision Boundary

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
                     np.arange(y_min, y_max, 0.1))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.figure(figsize=(10, 8))
plt.contourf(xx, yy, Z, alpha=0.4, cmap='RdYlBu')
scatter = plt.scatter(X[:, 0], X[:, 1], c=y, cmap='RdYlBu', edgecolor='black')
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.title("Multiclass Logistic Regression Decision Boundary")
plt.colorbar(scatter)
plt.show()

登录后复制

This block visualizes the decision boundaries created by the logistic regression model, illustrating how the model separates the three classes in the feature space.

Output:

Logistic Regression Multiclass Classification

This structured approach demonstrates how to implement and evaluate logistic regression for multiclass classification tasks, providing a clear understanding of its capabilities and the effectiveness of visualizing decision boundaries.

Evaluating Logistic Regression Model

Evaluating a logistic regression model involves assessing its performance in predicting binary or multiclass outcomes. Below are key methods for evaluation:

1. Performance Metrics

Accuracy: The proportion of correctly classified instances out of the total instances. It provides a general sense of the model's performance.
- Formula: Accuracy = (TP + TN) / (TP + TN + FP + FN)

  from sklearn.metrics import accuracy_score

  accuracy = accuracy_score(y_test, y_pred)
  print(f'Accuracy: {accuracy:.4f}')

登录后复制

Confusion Matrix: A table that summarizes the performance of the classification model by showing the true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN).

  from sklearn.metrics import confusion_matrix

  conf_matrix = confusion_matrix(y_test, y_pred)
  print("\nConfusion Matrix:")
  print(conf_matrix)

登录后复制

Precision: Measures the accuracy of the positive predictions. It is the ratio of true positives to the sum of true and false positives.
- Formula: Precision = TP / (TP + FP)

  from sklearn.metrics import precision_score

  precision = precision_score(y_test, y_pred, average='weighted')
  print(f'Precision: {precision:.4f}')

登录后复制

Recall (Sensitivity): Measures the model's ability to identify all relevant instances (true positives). It is the ratio of true positives to the sum of true positives and false negatives.
- Formula: Recall = TP / (TP + FN)

  from sklearn.metrics import recall_score

  recall = recall_score(y_test, y_pred, average='weighted')
  print(f'Recall: {recall:.4f}')

登录后复制

F1 Score: The harmonic mean of precision and recall, providing a balance between the two metrics. It is useful when the class distribution is imbalanced.
- Formula: F1 Score = 2 * (Precision * Recall) / (Precision + Recall)

  from sklearn.metrics import f1_score

  f1 = f1_score(y_test, y_pred, average='weighted')
  print(f'F1 Score: {f1:.4f}')

登录后复制

2. Cross-Validation

Cross-validation techniques provide a more reliable evaluation of model performance by assessing it across different subsets of the dataset.

K-Fold Cross-Validation: The dataset is divided into k subsets, and the model is trained on k-1 subsets while validating on the remaining subset. This is repeated k times, and the average metric provides a robust evaluation.

  from sklearn.model_selection import KFold, cross_val_score

  kf = KFold(n_splits=5, shuffle=True, random_state=42)
  scores = cross_val_score(model, X, y, cv=kf, scoring='accuracy')
  print(f'Cross-Validation Accuracy: {np.mean(scores):.4f}')

登录后复制

Stratified K-Fold Cross-Validation: Similar to K-Fold but ensures that each fold maintains the class distribution, which is particularly beneficial for imbalanced datasets.

  from sklearn.model_selection import StratifiedKFold

  skf = StratifiedKFold(n_splits=5)
  scores = cross_val_score(model, X, y, cv=skf, scoring='accuracy')
  print(f'Stratified K-Fold Cross-Validation Accuracy: {np.mean(scores):.4f}')

登录后复制

By utilizing these evaluation methods and cross-validation techniques, practitioners can gain insights into the effectiveness of their logistic regression model and its ability to generalize to unseen data.

Regularization in Logistic Regression

Regularization helps mitigate overfitting in logistic regression by adding a penalty term to the loss function, encouraging simpler models. The two primary forms of regularization in logistic regression are L1 regularization (Lasso) and L2 regularization (Ridge).