中科大联合华为诺亚提出Entropy Law，揭秘大模型性能、数据压缩率以及训练损失关系

AIxiv专栏是本站发布学术、技术内容的栏目。过去数年，本站AIxiv专栏接收报道了2000多篇内容，覆盖全球各大高校与企业的顶级实验室，有效促进了学术交流与传播。如果您有优秀的工作想要分享，欢迎投稿或者联系报道。投稿邮箱：liyazhou@jiqizhixin.com；zhaoyunfeng@jiqizhixin.com

本工作由中科大认知智能全国重点实验室 IEEE Fellow 陈恩红团队与华为诺亚方舟实验室完成。陈恩红教授团队深耕数据挖掘、机器学习领域，在顶级期刊与会议上发表多篇论文，谷歌学术论文引用超两万次。诺亚方舟实验室是华为公司从事人工智能基础研究的实验室，秉持理论研究与应用创新并重的理念，致力于推动人工智能领域的技术创新和发展。

数据是大语言模型（LLMs）成功的基石，但并非所有数据都有益于模型学习。直觉上，高质量的样本在教授 LLM 上预期会有更好的效率。因此，现有方法通常专注于基于质量的数据选择。然而，这些方法中的大多数独立地评估不同的数据样本，忽略了样本之间复杂的组合效应。如图 1 所示，即使每个样本质量完美，由于它们的互信息冗余或不一致性，它们的组合可能仍然次优。尽管基于质量的子集由所有三个优质样本组成，但它们编码的知识实际上是冗余和冲突的。相比之下，另一个由几个相对较低质量但多样化的样本组成的数据子集在教授 LLM 方面可能传达更多信息。因此，基于质量的数据选择并未完全符合最大化 LLM 知识掌握的目标。

而本文旨在揭示 LLM 性能与数据选择之间的内在关系。受 LLM 信息压缩本质的启发，我们发现了一条 entropy law，它将 LLM 性能与数据压缩率和前几步模型训练的损失加以联系，分别反映了数据集的信息冗余程度和 LLM 对数据集中固有知识的掌握程度。通过理论推导和实证评估，我们发现模型性能与训练数据的压缩率呈负相关，而这通常会产生较低的训练损失。基于 entropy law 的发现，我们提出了一种非常高效且通用的数据选择方法用于训练 LLM，名为 ZIP，其旨在优先选择低压缩率的数据子集。ZIP 分多阶段、贪心地选择多样化的数据，最终获得一个具有良好多样性的数据子集。

• 团队：中科大认知智能全国重点实验室陈恩红团队，华为诺亚方舟实验室
• 论文链接: https://arxiv.org/pdf/2407.06645
• 代码链接: https://github.com/USTC-StarTeam/ZIP

O 図 1 tENTropy の法則

データ圧縮と LLM パフォーマンスの関係を理論的に分析します。直観的には、トレーニング データの正確さと多様性が最終モデルのパフォーマンスに影響します。同時に、データに重大な固有の矛盾がある場合、またはモデルがデータにエンコードされた情報を十分に把握していない場合、LLM のパフォーマンスは最適ではない可能性があります。これらの仮定に基づいて、LLM のパフォーマンスを Z として表します。これは次の影響を受けると予想されます。

データ圧縮率 R: 直感的には、圧縮率が低いデータセットは情報密度が高いことを示します。

トレーニング損失 L: モデルがデータを記憶するのが難しいかどうかを示します。同じ基本モデルの下で、高いトレーニング損失が発生するのは、通常、データセット内のノイズや一貫性のない情報の存在が原因です。

• データの一貫性 C: データの一貫性は、前の状況を考慮した次のトークンの確率のエントロピーによって反映されます。通常、データの一貫性が高いほど、トレーニング損失が少なくなります。
• 平均データ品質 Q: データのサンプルレベルの平均品質を反映しており、さまざまな客観的および主観的な側面を通じて測定できます。
• 一定量のトレーニング データが与えられると、モデルのパフォーマンスは上記の要素によって推定できます。

ここで、f は暗黙の関数です。特定の基本モデルが与えられると、L のスケールは通常 R と C に依存し、次のように表すことができます:

均一性が高い、またはデータの一貫性が高いデータセットはモデルによって学習されやすいため、L は次のように表されます。 R と C では単調であると予想されます。したがって、上記の式は次のように書き換えることができます:

ここで、g' は逆関数です。上記の 3 つの方程式を組み合わせると、次のようになります:

其中 h 是另一个隐函数。如果数据选择方法不会显着改变平均数据质量 Q，我们可以近似地将变量 Q 视为常数。因此，最终性能可以粗略地表示为：

这意味着模型性能与数据压缩率和训练损失相关。我们将这种关系称为 Entropy law。

基于 Entropy law，我们提出两个推论：

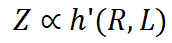
• 如果将 C 视为常数，训练损失直接受压缩率影响。因此，模型性能由压缩率控制：如果数据压缩率 R 较高，那么 Z 通常较差，这将在我们的实验中得到验证。
• 在相同的压缩率下，较高训练损失意味着较低的数据一致性。因此，模型学到的有效知识可能更有限。这可以用来预测 LLM 在具有相似压缩率和样本质量的不同数据上的性能。我们将在后续展示这一推论在实践中的应用。

ZIP：高度轻量化的数据选择算法

在entropy law 的指导下，我们提出了ZIP 这一数据选择方法，通过数据压缩率来选择数据样本，旨在在有限的训练数据预算下最大化有效信息量。出于效率考量，我们采用了一种迭代多阶段贪心范式，以高效地获得具有相对低压缩率的近似解。在每轮迭代中，我们首先使用全局选择阶段来选择一组具有低压缩率的候选样本池，找到信息密度高的样本。然后，我们采用粗粒度的局部选择阶段，选择一组与已选样本冗余度最低的较小样本集。最后，我们使用细粒度的局部选择阶段，最小化要添加样本之间的相似性。上述过程持续进行直到获得足够的数据，具体算法如下：

实验结果

1.ZIP 选择算法对于不同LLM、在不同LLM 对齐阶段的有效性

对比不同的SFT 数据选择算法，基于ZIP 选择数据所训练得到的模型性能上展现出优势，并且在效率上也占优。具体结果见下表：

得益于 ZIP 的模型无关、内容无感知的特性，其同样也可应用于偏好对齐阶段的数据选择。而 ZIP 所选择的数据同样展现出了较大的优势。具体结果见下表：

2.Entropy law 的实验验证

基于SFT 数据选择实验，我们基于模型效果、数据压缩率以及模型在前几步训练的损失，分别拟合了多条关系曲线。结果见图 2 以及图 3，我们从图中可以观察到三个因素之间的紧密关联。首先，低压缩率数据通常会带来更好的模型效果，这是因为LLMs 的学习过程与信息压缩高度相关，我们可以将LLM 视为数据压缩器，那么压缩率较低的数据意味着更多的知识量，从而对压缩器更有价值。同时，可以观察到较低的压缩率通常伴随着更高的训练损失，这是因为难以压缩的数据携带了更多的知识，对 LLM 吸收其中蕴含的知识提出了更大的挑战。

                               ^{图 2 Mistral-7B}

図 3 Llama-3-8B

実際のシナリオ アプリケーションにおける LLM トレーニング データの増分更新をガイドするエントロピー則を提供します。このタスク シナリオでは、トレーニング データの量は比較的安定しており、データのごく一部のみが変更されます。結果を図 4 に示します。ここで、 から ^{は段階的に更新される 5 つのデータ バージョンです。機密性の要件により、異なる圧縮率でのモデル効果の相対的な関係のみが示されています。エントロピーの法則の予測によれば、各増分更新後にデータ品質が大幅に低下しないと仮定すると、データ圧縮率が低下するにつれてモデルのパフォーマンスが向上することが期待できます。この予測は、図のデータ バージョン} から の結果と一致しています。ただし、データ バージョン

では損失とデータ圧縮率が異常に増加しており、トレーニング データの一貫性の低下によりモデルのパフォーマンスが低下する可能性があることを示しています。この予測は、その後のモデルの性能評価によってさらに確認されました。したがって、エントロピーの法則は、LLM トレーニングの指針として機能し、収束するまで完全なデータセットでモデルをトレーニングしなくても、LLM トレーニングの失敗の潜在的なリスクを予測できます。 LLM のトレーニングにかかる​​コストが高いことを考えると、これは特に重要です。

以上是中科大联合华为诺亚提出Entropy Law，揭秘大模型性能、数据压缩率以及训练损失关系的详细内容。更多信息请关注PHP中文网其他相关文章！