
AIxiv专栏是本站发布学术、技术内容的栏目。过去数年,本站AIxiv专栏接收报道了2000多篇内容,覆盖全球各大高校与企业的顶级实验室,有效促进了学术交流与传播。如果您有优秀的工作想要分享,欢迎投稿或者联系报道。投稿邮箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com



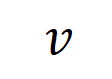 和一个输入样本
和一个输入样本 ,它包含
,它包含 个输入变量,我们用集合
个输入变量,我们用集合 表示这些输入变量的全集。令
表示这些输入变量的全集。令 表示 DNN 在样本
表示 DNN 在样本 上的一个标量输出。对于一个面向分类任务的神经网络,我们可以从不同角度来定义其标量输出。例如,对于多类别分类问题,
上的一个标量输出。对于一个面向分类任务的神经网络,我们可以从不同角度来定义其标量输出。例如,对于多类别分类问题, 可以定义为
可以定义为 ,也可以定义为 softmax 层之前该样本真实标签所对应的标量输出。这里,
,也可以定义为 softmax 层之前该样本真实标签所对应的标量输出。这里, 表示真实标签的分类概率。这样,针对每个子集
表示真实标签的分类概率。这样,针对每个子集 ,我们可以用下面公式来定义
,我们可以用下面公式来定义 中所有输入变量之间 “等效与交互” 和 “等效或交互”。
中所有输入变量之间 “等效与交互” 和 “等效或交互”。
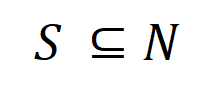 内输入变量之间的 “与关系”。例如,给定一个输入句子
内输入变量之间的 “与关系”。例如,给定一个输入句子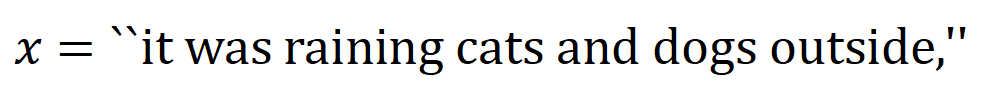 ,神经网络可能会在
,神经网络可能会在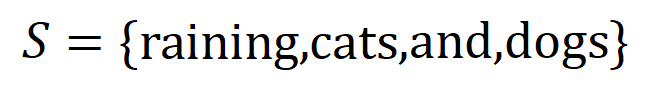 之间建模一个交互,使得
之间建模一个交互,使得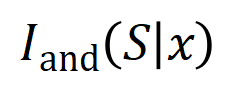 产生一个推动神经网络输出 “倾盆大雨” 的数值效用。如果
产生一个推动神经网络输出 “倾盆大雨” 的数值效用。如果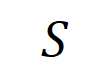 中的任何输入变量被遮挡,则该数值效用将从神经网络的输出中移除。类似地,等效或交互
中的任何输入变量被遮挡,则该数值效用将从神经网络的输出中移除。类似地,等效或交互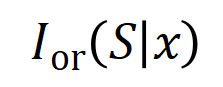 表示神经网络所建模的
表示神经网络所建模的 内输入变量之间的 “或关系”。例如,给定一个输入句子
内输入变量之间的 “或关系”。例如,给定一个输入句子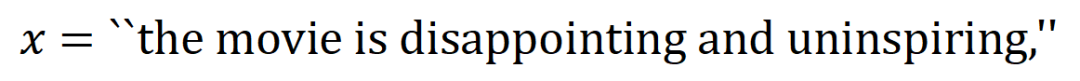 ,只要
,只要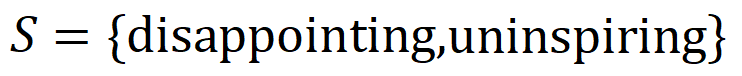 中的任意一个词出现,就会推动神经网络的输出负面情感分类。
中的任意一个词出现,就会推动神经网络的输出负面情感分类。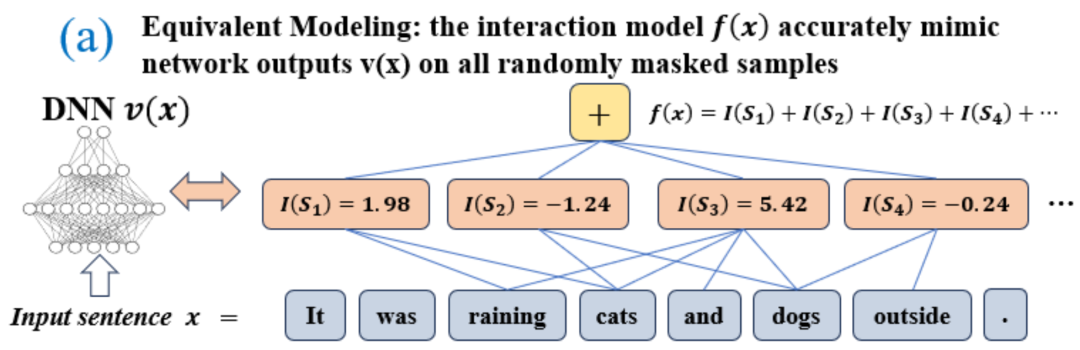
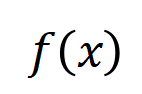 准确拟合。每个交互都是衡量神经网络建模特定输入变量集合
准确拟合。每个交互都是衡量神经网络建模特定输入变量集合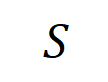 之间非线性关系的度量指标。当且仅当集合中变量同时出现时才会触发与交互,并为输出贡献数值分数
之间非线性关系的度量指标。当且仅当集合中变量同时出现时才会触发与交互,并为输出贡献数值分数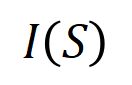 ,集合
,集合 中任意变量出现时会触发或交互。
中任意变量出现时会触发或交互。
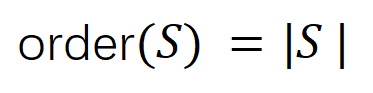 。我们团队之前的工作发现神经网络在某个特定样本所建模的 “与或交互” 的复杂度直接决定了神经网络在这个样本的泛化能力 [1],即神经网络建模的高阶的(大量输入单元之间的)“与或交互” 往往有较差的泛化能力,而低阶的(少量输入单元之间的)“与或交互” 具有较强的泛化能力。
。我们团队之前的工作发现神经网络在某个特定样本所建模的 “与或交互” 的复杂度直接决定了神经网络在这个样本的泛化能力 [1],即神经网络建模的高阶的(大量输入单元之间的)“与或交互” 往往有较差的泛化能力,而低阶的(少量输入单元之间的)“与或交互” 具有较强的泛化能力。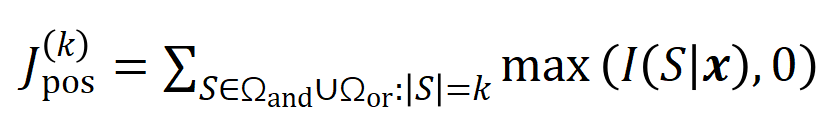 来衡量所有阶正显著交互的强度,用
来衡量所有阶正显著交互的强度,用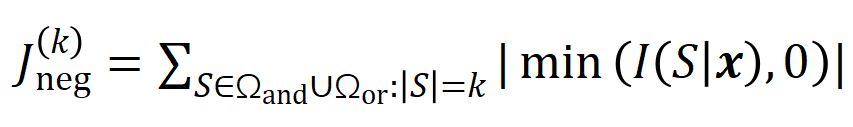 来衡量所有
来衡量所有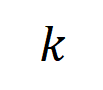 阶负显著交互的强度,其中
阶负显著交互的强度,其中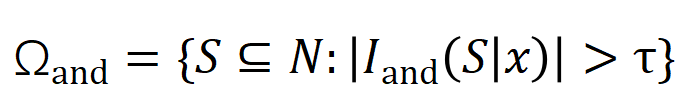 和
和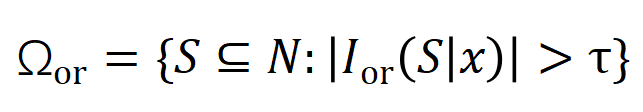 表示显著交互的集合,
表示显著交互的集合, 表示显著交互的阈值。
表示显著交互的阈值。
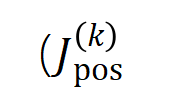 和
和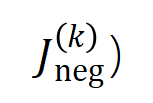 。在不同数据集上、不同任务上训练的不同的神经网络的训练过程都存在两阶段现象。前两个选定时间点属于第一阶段,而后两个时间点属于第二阶段。恰恰在进入神经网络训练过程的第二阶段不久,神经网络的测试损失和训练损失之间的 loss gap 开始显着上升(见最后一列)。这表明神经网络训练的两阶段现象与模型 loss gap 的变化在时间上是 “对齐” 的。更多实验结果请参见论文。
。在不同数据集上、不同任务上训练的不同的神经网络的训练过程都存在两阶段现象。前两个选定时间点属于第一阶段,而后两个时间点属于第二阶段。恰恰在进入神经网络训练过程的第二阶段不久,神经网络的测试损失和训练损失之间的 loss gap 开始显着上升(见最后一列)。这表明神经网络训练的两阶段现象与模型 loss gap 的变化在时间上是 “对齐” 的。更多实验结果请参见论文。 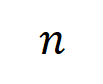 个输入变量的输入样本
个输入变量的输入样本 ,我们将从输入样本
,我们将从输入样本 提取到的
提取到的 阶交互向量化
阶交互向量化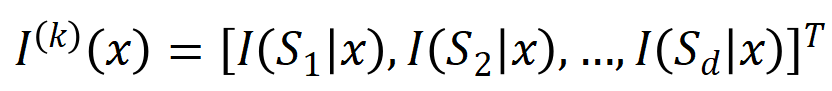 ,其中
,其中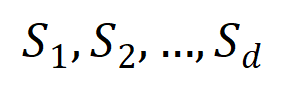 表示
表示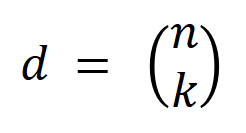 个
个 阶交互。然后,我们计算分类任务中所有类别为
阶交互。然后,我们计算分类任务中所有类别为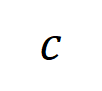 的样本中提取到的
的样本中提取到的 阶的平均交互向量,表示为
阶的平均交互向量,表示为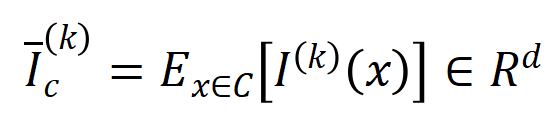 ,其中
,其中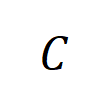 表示类别为
表示类别为 的样本的集合。接下来,我们计算从训练样本中提取的阶的平均交互向量
的样本的集合。接下来,我们计算从训练样本中提取的阶的平均交互向量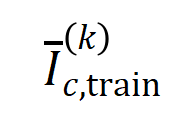 与从测试样本中提取的
与从测试样本中提取的 阶的平均交互向量
阶的平均交互向量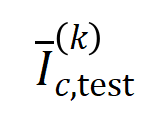 之间的 Jaccard 相似性,以衡量分类任务中类别为
之间的 Jaccard 相似性,以衡量分类任务中类别为 的样本的
的样本的 阶交互的泛化能力,即:
阶交互的泛化能力,即: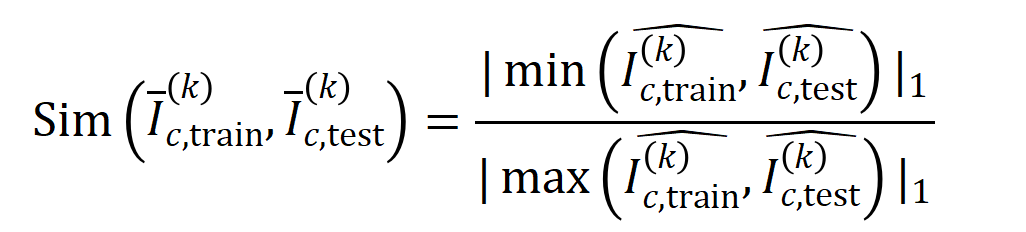
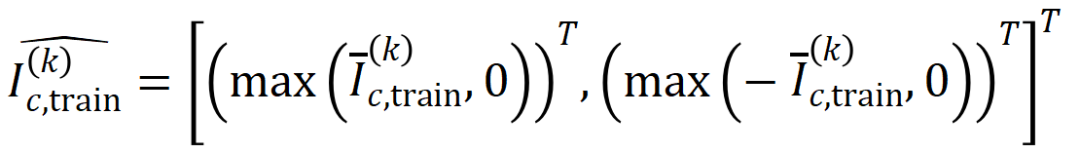 和
和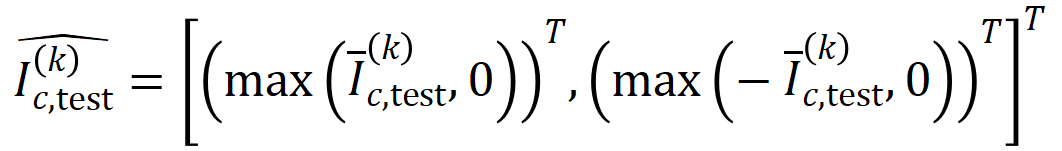 将两个
将两个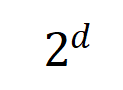 维交互向量投影到两个
维交互向量投影到两个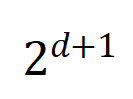 维的非负向量上,以便计算 Jaccard 相似性。对于某一阶的交互,如果此阶交互普遍展现出较大的 Jaccard 相似性,则表示这一阶交互具有较强的泛化能力。
维的非负向量上,以便计算 Jaccard 相似性。对于某一阶的交互,如果此阶交互普遍展现出较大的 Jaccard 相似性,则表示这一阶交互具有较强的泛化能力。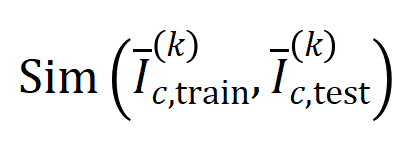 。我们测试了在 MNIST 数据集上训练的 LeNet、在 CIFAR-10 数据集上训练的 VGG-11、在 CUB200-2011 数据集上训练的 VGG-13,以及在 Tiny-ImageNet 数据集上训练的 AlexNet。为了减少计算成本,我们仅计算了前 10 个类别的 Jaccard 相似性的平均值
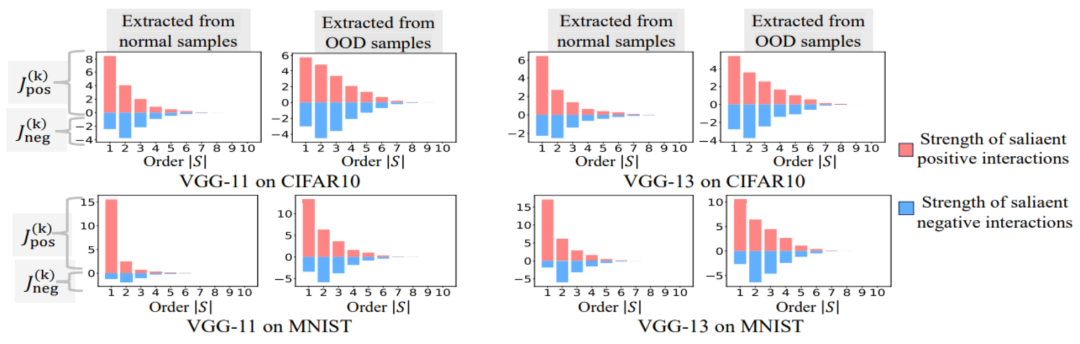
。我们测试了在 MNIST 数据集上训练的 LeNet、在 CIFAR-10 数据集上训练的 VGG-11、在 CUB200-2011 数据集上训练的 VGG-13,以及在 Tiny-ImageNet 数据集上训练的 AlexNet。为了减少计算成本,我们仅计算了前 10 个类别的 Jaccard 相似性的平均值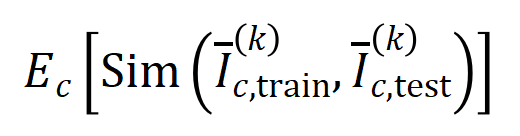 。如图 7 所示,随着交互阶数的增加,交互的 Jaccard 相似性不断下降。因此,这验证了高阶交互比低阶交互具有更差的泛化能力。
。如图 7 所示,随着交互阶数的增加,交互的 Jaccard 相似性不断下降。因此,这验证了高阶交互比低阶交互具有更差的泛化能力。 图 7:从训练样本和测试样本中提取的交互之间的 Jaccard 相似性。低阶交互具有相对较高 Jaccard 相似性表明低阶交互具有较强的泛化能力。
图 7:从训练样本和测试样本中提取的交互之间的 Jaccard 相似性。低阶交互具有相对较高 Jaccard 相似性表明低阶交互具有较强的泛化能力。
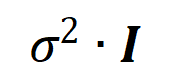
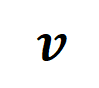 を、さまざまなインタラクション トリガー関数の重み付き合計 として書き換えます。
を、さまざまなインタラクション トリガー関数の重み付き合計 として書き換えます。  ここで、
ここで、  は
は  を満たすスカラー重みです。関数
を満たすスカラー重みです。関数  は対話型トリガー関数であり、任意のオクルージョン サンプル
は対話型トリガー関数であり、任意のオクルージョン サンプル  で
で  を満たします。関数
を満たします。関数  の具体的な形式については、論文を参照してください。ここでは説明しません。
の具体的な形式については、論文を参照してください。ここでは説明しません。
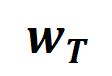 の学習と近似できる。さらに、研究室の予備研究 [3] では、同じタスクで完全にトレーニングされた異なるニューラル ネットワークは同様の相互作用をモデル化する傾向があることが判明したため、ニューラル ネットワークの学習は一連の潜在的なグラウンド トゥルース相互作用とみなすことができます。したがって、ニューラル ネットワークが収束するようにトレーニングされているときにモデル化された相互作用は、次の目的関数を最小化するときに得られる解とみなすことができます:
の学習と近似できる。さらに、研究室の予備研究 [3] では、同じタスクで完全にトレーニングされた異なるニューラル ネットワークは同様の相互作用をモデル化する傾向があることが判明したため、ニューラル ネットワークの学習は一連の潜在的なグラウンド トゥルース相互作用とみなすことができます。したがって、ニューラル ネットワークが収束するようにトレーニングされているときにモデル化された相互作用は、次の目的関数を最小化するときに得られる解とみなすことができます:  ここで、
ここで、 は、ニューラル ネットワークが適合する必要がある一連の潜在的なグランド トゥルース相互作用を表します。
は、ニューラル ネットワークが適合する必要がある一連の潜在的なグランド トゥルース相互作用を表します。  と
と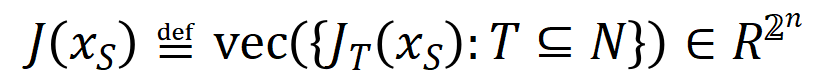 はそれぞれ、すべての重みをまとめて得られるベクトルと、すべてのインタラクショントリガー関数の値をまとめて得られるベクトルを表します。
はそれぞれ、すべての重みをまとめて得られるベクトルと、すべてのインタラクショントリガー関数の値をまとめて得られるベクトルを表します。
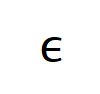 が満たされる場所
が満たされる場所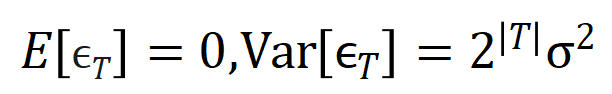 。そして、トレーニングが進むにつれて、ノイズ
。そして、トレーニングが進むにつれて、ノイズ 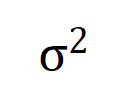 の分散は徐々に小さくなります。
の分散は徐々に小さくなります。  に対して上記の損失関数を最小化することにより、下図の定理に示すように、 最適な相互作用重み
に対して上記の損失関数を最小化することにより、下図の定理に示すように、 最適な相互作用重み  の解析解 を得ることができます。
の解析解 を得ることができます。 
 (図に示すように)以下の定理)。これは、トレーニングの第 2 フェーズ中にニューラル ネットワークが高次の相互作用を徐々に学習する現象を説明します。
(図に示すように)以下の定理)。これは、トレーニングの第 2 フェーズ中にニューラル ネットワークが高次の相互作用を徐々に学習する現象を説明します。 
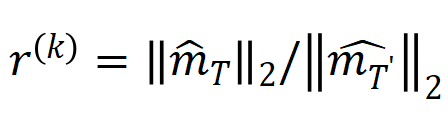 は
は 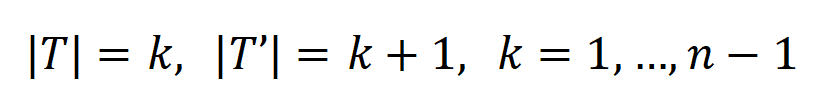 ) を使用して、k 次の相互作用と k+1 次の相互作用の強度の比を近似的に測定できます。下の図では、入力ユニットの数 n と次数 k が異なると、
) を使用して、k 次の相互作用と k+1 次の相互作用の強度の比を近似的に測定できます。下の図では、入力ユニットの数 n と次数 k が異なると、 が減少するにつれて比率が徐々に減少することがわかります。
が減少するにつれて比率が徐々に減少することがわかります。 
 徐々に減少します。これは、トレーニングが進むにつれて (つまり、
徐々に減少します。これは、トレーニングが進むにつれて (つまり、 が徐々に小さくなる)、低次の相互作用強度と高次の相互作用強度の比率が徐々に小さくなり、ニューラル ネットワークが徐々に高次の相互作用を学習することを示しています。
が徐々に小さくなる)、低次の相互作用強度と高次の相互作用強度の比率が徐々に小さくなり、ニューラル ネットワークが徐々に高次の相互作用を学習することを示しています。  の下での各次数での理論的な相互作用値の分布
の下での各次数での理論的な相互作用値の分布 を、実際のトレーニングプロセス中の相互作用の各次数の分布
を、実際のトレーニングプロセス中の相互作用の各次数の分布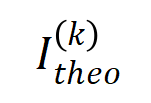 と比較し、理論 相互作用分布は、実際のトレーニングにおける各時点での相互作用強度分布を適切に予測できます。
と比較し、理論 相互作用分布は、実際のトレーニングにおける各時点での相互作用強度分布を適切に予測できます。 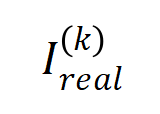

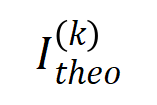 (青色のヒストグラム) と実際の相互作用分布
(青色のヒストグラム) と実際の相互作用分布 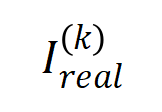 (オレンジ色のヒストグラム) の比較。理論的な相互作用分布は、トレーニングの第 2 フェーズのさまざまな時点での実際の相互作用分布を適切に予測し、一致させます。詳しい結果については論文を参照してください。
(オレンジ色のヒストグラム) の比較。理論的な相互作用分布は、トレーニングの第 2 フェーズのさまざまな時点での実際の相互作用分布を適切に予測し、一致させます。詳しい結果については論文を参照してください。 
 が徐々に減少するときの重み の最適解の変化として説明できる場合、最初の段階は次のようになります。初期のランダムな相互作用は、徐々に最適解に収束します。
が徐々に減少するときの重み の最適解の変化として説明できる場合、最初の段階は次のようになります。初期のランダムな相互作用は、徐々に最適解に収束します。
等価相互作用理論システム
[1] Huiqi Deng、Na Zou、Mengnan Du、Weifu Chen、Guocan Feng 、 Ziwei Yang、Zheyang Li、Quanshi Zhang、14 のポストホック アトリビューション メソッドとテイラー インタラクションの統合、パターン分析とマシン インテリジェンスに関する IEEE トランザクション (IEEE T-PAMI)、2024 年。
[2] Xu Cheng、Lei Cheng 、Zhaoran Peng、Yang Xu、Tian Han、Quanshi Zhang、ICML における層ごとの知識の変化。
[3] Qihan Ren、Jiayang Gao、Wen Shen、Quanshi Zhang。 AI モデルにおけるスパース インタラクション プリミティブの証明、2024 年。
[4] Lu Chen、Siyu Lou、Benhao Huang、Quanshi Zhang、ICLR からの一般化可能なインタラクション プリミティブの定義、2024 年。
[5] Huilin Zhou、Hao Zhang、Huiqi Deng、Dongrui Liu、Wen Shen、Shih-Han Chan、Quanshi Zhang、AAAI、2024 年。
[ 6 ] Dongrui Liu、Huiiqi Deng、Xu Cheng、Qihan Ren、Kangrui Wang、Quanshi Zhang、さまざまな複雑さの概念を学習するディープ ニューラル ネットワークの困難に向けて、2023 年。
[7] Quanshi Zhang、Jie Ren、Ge Huang、Ruiming Cao、Ying Nian Wu、Song-Chun Zhu。アクティブ質問応答による畳み込みネットワークからの解釈可能な AOG 表現のマイニング。パターン分析とマシン インテリジェンスに関する IEEE トランザクション (IEEE T)。 -PAMI)、2020年。
[8] Xin Wang、Jie Ren、Shuyun Lin、Xiangming Zhu、Yisen Wang、Quanshi Zhang、ICLR、2021年。 [9] Hao Zhang、Sen Li、Yinchao Ma、Mingjie Li、Yichen Xie、Quanshi Zhang、ICLR の解釈と強化、2021 年。
[10] Mingjie Li、Quanshi Zhang。ニューラル ネットワークは本当にシンボリック コンセプトをエンコードしますか? ICML、2023.
[12] Qihan Ren、Huiqi Deng、Yunuo Chen、Siyu Lou、Quanshi Zhang、ベイジアン ニューラル ネットワークは摂動に敏感な複雑な概念を回避します。
[13] ] Jie Ren、Mingjie Li、Qirui Chen、Huiqi Deng、Quanshi Zhang、DNN におけるスパース概念の出現の定義と定量化、2023 年。
[14] Jie Ren、Mingjie Li、Meng Zhou、Shih- Han Chan、Quanshi Zhang、ReLU DNN の変換の複雑さの理論的分析に向けて、2022 年
[15] Jie Ren、Die Zhang、Yisen Wang、Lu Chen、Zhanpeng Zhou、Yiting Chen、Xu Cheng、Xin Wang、Meng Zhou、Jie Shi、Quanshi Zhang、NeurIPS の統一ゲーム理論的解釈。Wen Shen、Qihan Ren、Dongrui Liu、Quanshi Zhang の表現品質の解釈。 3D 点群処理のための DNN、2021 年。
[17] Xin Wang、Shuyun Lin、Hao Zhang、Yufei Zhu、Quanshi Zhang、2021 年。] Wen Shen、 Zhihua Wei、Shikun Huang、Binbin Zhang、Panyue Chen、Ping Zhao、Quanshi Zhang、検証可能性と予測可能性: 3D 点群処理のためのネットワーク アーキテクチャの解釈、2021 年。
[19] Hao Zhang、Yichen Xie。 、Longjie Zheng、Die Zhang、Quanshi Zhang、DNN での多変量 Shapley 相互作用の解釈、2021 年。 Mengyue Wu、Quanshi Zhang、ディープ NLP モデルのための解釈可能なインタラクション ツリーの構築、2021 年。
以上是可解释性终极追问,什么才是第一性解释?20篇CCF-A+ICLR论文给你答案的详细内容。更多信息请关注PHP中文网其他相关文章!




