您可以将计算斐波那契数列的程序优化到什么程度？

您可以将计算斐波那契数列的程序优化到什么程度？

介绍

我学Python的时候，老师给我们布置了一个作业——计算斐波那契数列的第N个数。

我觉得很简单，所以我写了这段代码：

def fib(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fib(n - 1) + fib(n - 2)

后来我知道这种解决方案太费时间了。

优化程序

我将解决方案更改为迭代。

def fib(n):
    ls = [1,1]
    for i in range(2,n):
        ls.append(ls[i-1]+ls[i-2])

    return ls[n-1]

我使用matplotlib绘制它花费的时间：

import time
import matplotlib.pyplot as plt


def bench_mark(func, *args):
    # calculate the time
    start = time.perf_counter()
    result = func(*args)
    end = time.perf_counter()

    return end - start, result  # return the time and the result

def fib(n):
    ls = [1,1]
    for i in range(2,n):
        ls.append(ls[i-1]+ls[i-2])

    return ls[n-1]

mark_list = []

for i in range(1,10000):
    mark = bench_mark(fib,i)
    mark_list.append(mark[0])
    print(f"size : {i} , time : {mark[0]}")

plt.plot(range(1, 10000), mark_list)
plt.xlabel('Input Size')
plt.ylabel('Execution Time (seconds)')
plt.title('Test fot fibonacci')
plt.grid(True)
plt.show()

结果在这里：

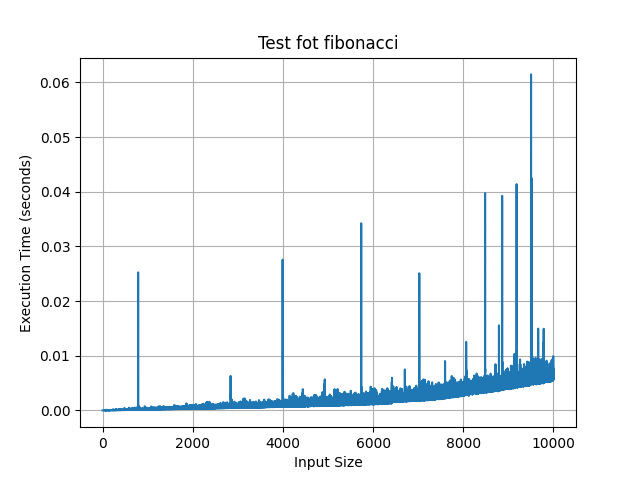
花费的时间很短。

但是我写了 fib(300000)，花费了 5.719049899998936 秒。太长了。

长大后，我学会了CACHE，所以我改变解决方案，使用dict来存储结果。

from functools import lru_cache
@lru_cache(maxsize=None)
def fib(n):
    if n < 2:
        return 1
    else:
        return fib(n - 1) + fib(n - 2)

或者我们可以自己写CACHE。

def fib(n, cache={}):
    if n in cache:
        return cache[n]
    elif n < 2:
        return 1
    else:
        ls = [1, 1]
        for i in range(2, n):
            next_value = ls[-1] + ls[-2]
            ls.append(next_value)
            cache[i] = next_value
        cache[n-1] = ls[-1]
        return ls[-1]

以上是您可以将计算斐波那契数列的程序优化到什么程度？的详细内容。更多信息请关注PHP中文网其他相关文章！