Java 中的排序算法

按照一定的顺序对信息进行排序，通常是在类似数组的框架内，就是对它们进行排列。您可以使用不同的顺序要求；流行的方法是将数字从小到大排序，反之亦然，或者按字典顺序对字符串排序。如果您对排序的工作原理感兴趣，我们将介绍不同的算法，从无效但直观的替代方案到用 Java 和其他语言有效实现的高效算法。

java中不同的排序算法

有不同的排序算法，但并非所有算法都同样有效。为了比较它们并看看哪些表现最好，我们将分析它们的时间复杂度。

广告 该类别中的热门课程 JAVA 掌握 - 专业化 | 78 课程系列 | 15 次模拟测试

1. 插入排序
2. 冒泡排序
3. 选择排序
4. 合并排序
5. 堆排序

1.插入排序

插入排序背后的概念将范围划分为已排序和未排序的子数组。分类部分位于持续时间 1 的开始处，并与数组中的第一个（左侧）组件匹配。我们遍历数组，并在每次迭代期间将数组的分类部分扩展一个分量。当我们扩展时，我们将新元素放置在已排序的子数组中。为此，我们将所有元素向右移动，直到发现不必更改第一个组件。当粗体部分按升序排序时，例如在下面的数组中，会出现：

1. 3 5 7 8 4 2 1 9 6：考虑 4 并插入这就是我们需要的。我们从 8 > 开始就一直在转移。 4
2. 2. 3 5 7 x 8 2 1 9 6
3. 3 5 x 7 8 2 1 9 6
4. 3 x 5 7 8 2 1 9 6
5. 3 4 5 7 8 2 1 9 6

代码：

public class InsertionSortEx {
public static void insertionSort(int[] arr) {
for (int x = 1; x < arr.length; x++) {
int current = arr[x];
int y = x - 1;
while(y >= 0 && current < arr[y]) {
arr[y+1] = arr[y];
y--;
}
arr[y+1] = current;
}
}
public static void main(String a[]){
int[] arr1 = {3,5,7,8,4,2,1,9,6};
System.out.println("Before Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
System.out.println();
insertionSort(arr1);//sorting array using insertion sort
System.out.println("After Insertion Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
}
}

输出：

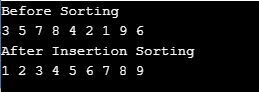
按照这个方法，一个组件扩展了排序后的部分；我们现在有五个而不是四个元素。每次迭代都会执行此操作，整个数组将按末尾排序。

注意：这是因为我们需要在每次迭代中将整个分类列表一一传输，时间复杂度为 O(n)。我们必须对每个表中的每个组件执行此操作，这意味着它是 O(n^2) 有界的。2。

2.冒泡排序

如果气泡不符合要求的顺序，它会通过更换相邻组件来运行。重复此操作，直到所有组件从数组的开头开始按顺序排列。我们知道，如果我们设法在不进行交换的情况下完成整个迭代，则与相邻元素相比的所有项目都处于所需的顺序，并且通过扩展，整个数组也处于所需的顺序。冒泡排序算法的原因是像“冒泡”这样的数字进入“地面”。如果在特定数量之后，您再次浏览该实例（4 是一个很好的实例），您会注意到数字慢慢向右移动。

冒泡排序的步骤如下：

1. 4 21 5 3：这里，1^st 两个数字的顺序不正确；因此我们必须对这两个数字进行排序。
2. 2 4 15 3：之后，下一对数字的顺序也不正确。所以排序再次发生。
3. 2 1 4 53：这两个顺序正确，4
3 5，因此无需交换它们。
4. 2 1 4 5 3
：同样，我们必须交换正确的顺序。
2 1 4 3 5：这是一次迭代后的结果数组。
我们必须再次重复这个过程，直到数字排列正确。

代码：

public class BubbleSortExample {
public static void bubbleSort(int[] arr) {
int n = arr.length;
int tmp = 0;
for(int x=0; x < n; x++){
for(int y=1; y < (n-x); y++){
if(arr[y-1] > arr[y]){
//swap elements
tmp = arr[y-1];
arr[y-1] = arr[y];
arr[y] = tmp;
}
}
}
}
public static void main(String[] args) {
int arr[] ={4,2,1,5,3};
System.out.println("Array Before Bubble Sort");
for(int x=0; x < arr.length; x++){
System.out.print(arr[x] + " ");
}
System.out.println();
bubbleSort(arr);
System.out.println("Array After Bubble Sort");
for(int x=0; x < arr.length; x++){
System.out.print(arr[x] + " ");
}
}
}

输出：

注意：

如果我使用 a[i]>= a[i+1 ]，它可能会陷入无限循环，因为该连接对于等效组件仍然有效，因此始终将它们从一个组件交换元素到另一个。

3.选择排序

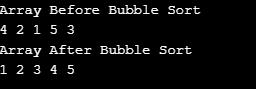
选择排序将数组拆分为未排序的分类数组。然而，这一次，排序子数组是通过交换在已排序数组的末尾插入未排序子数组的最小元素而形成的：

1. 3 5 1
2 4
2. 15 3 2
 4
3. 1 23
 5 4
4. 1 2 35 4
5. 1 2 3 45
6. 1 2 3 4 5

代码：

public class SelectionSortEx {
public static void selectionSort(int[] arr){
for (int x = 0; x < arr.length - 1; x++)
{
int indx = x;
for (int y = x + 1; y < arr.length; y++){
if (arr[y] < arr[indx]){
indx = y;
}
}
int smallNumber = arr[indx];
arr[indx] = arr[x];
arr[x] = smallNumber;
}
}
public static void main(String a[]){
int[] arr1 = {3,5,1,2,4};
System.out.println("Before Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
System.out.println();
selectionSort(arr1);
System.out.println("After Selection Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
}
}

输出：

<🎜> Note: The minimum is O(n) for the array size because all the components must be checked. For each element of the array, we must find the minimum and make the whole process O (n^2) limited.

4. Merge Sort

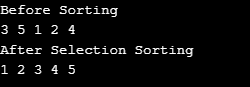
Merge Sort utilizes recursion to fix the issue of the divide and conquest method more effectively than earlier described algorithms.

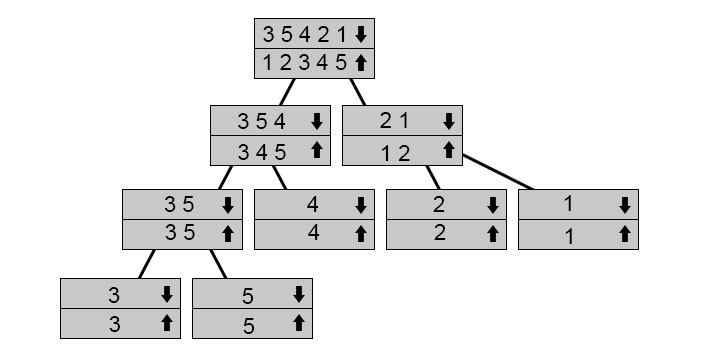
This tree shows how the recursive calls function. Down arrow marked arrays are the arrays for which we call function while we fuse up arrow arrays. Then you follow the arrow to the tree’s edge and then return and merge. We’ve got 3 5 3 1 range, so we split it into 3 5 4 and 2 1. We split them into their parts in order to sort them. We begin fusioning and sorting them as we go when we get to the bottom.

Code:

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
public class MergeSort {
static void merge(int[] array,int lowval,int midval,int highval){
int x, y ,k;
int[] c= new int[highval-lowval+1];
k = 0;
x=lowval;
y=midval+1;
while(x<=midval && y<=highval){
if(array[x]<=array[y]){
c[k++] = array[x++];
}
else{
c[k++] = array[y++];
}
}
while(x<=midval){
c[k++] = array[x++];
}
while(y<=highval){
c[k++] = array[y++];
}
k=0;
for(x = lowval; x<=highval; x++){
array[x] = c[k++];
}
}
static void mergeSort(int[] array,int lowval, int highval){
if(highval-lowval+1>1){
int midval = (lowval+highval)/2;
mergeSort(array,lowval,midval);
mergeSort(array,midval+1,highval);
merge(array,lowval,midval,highval);
}
}
public static void main(String[] args) {
BufferedReader r = new BufferedReader(new InputStreamReader(System.in));
int size;
System.out.println("Enter the array");
try {
size = Integer.parseInt(r.readLine());
} catch (Exception e) {
System.out.println("Please Enter valid Input");
return;
}
int[] array = new int[size];
System.out.println("Enter array elements");
int x;
for (x = 0; x < array.length; x++) {
try {
array[x] = Integer.parseInt(r.readLine());
} catch (Exception e) {
System.out.println("An error Occurred");
}
}
System.out.println("After Sorting");
System.out.println(Arrays.toString(array));
mergeSort(array,0,array.length-1);
System.out.println("Before Merge Sorting");
System.out.println(Arrays.toString(array));
}
}

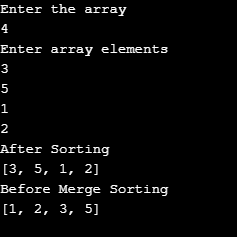
In this program, we have asked the user to enter input. The output will be in sorted order based on the user’s input.

Output:

5. Heap Sort

You first must know the framework on which Heapsort operates-the heap-in order to comprehend why it operates. We will specifically speak about a binary heap, but you can also generalize this to other heap constructions. A heap is a tree that fulfills the property of the heap, namely that all its kids have relationships to each node. A heap must also be nearly finished. A near-complete d-depth binary has a d-1 subtree with the same root, and each node has a full, left subtree, with a left descending.

In other words, you get a lower and lower number (min-heap) or larger and bigger (max-heap) when moving down the tree. Here is a max-heap instance:

1. 6 1 8 3 5 2 4: Here, Both children’s numbers are smaller than the parent; hence we do not have to change anything.
2. 6 1 8 3 52 4: Here, 5 > 1, we need to swap them. We need to heapify for 5.
3. 6 5 8 3 12 4: Both of the children’s numbers are smaller; everything remains the same.
4. 6 5 83 1 2 4: Here, 8 > 6, hence we should swap them.
5. 8 5 6 3 1 2 4: After this iteration, we will get this result.

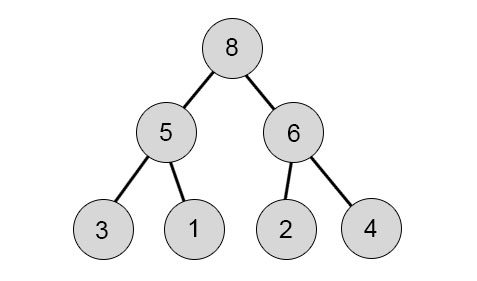
After Repeating this process again, we will get the following results:

• 8 5 6 3 1 2 4
1. 4 5 6 3 1 2 8: Swapping
2. 6 5 4 3 1 2 8: Heapify
3. 2 5 4 3 1 6 8: Swapping
4. 5 2 4 2 1 6 8: Heapify
5. 1 2 4 2 5 6 8: Swapping

Code:

public class HeapSort
{
public void sort(int arr[])
{
int n = arr.length;
for (int x = n / 2 - 1; x >= 0; x--)
heapify(arr, n, x);
for (int x=n-1; x>=0; x--)
int tmp = arr[0];
arr[0] = arr[x];
arr[x] = tmp;
heapify(arr, x, 0);
}
}
void heapify(int arr[], int n, int x)
{
int largest = x;
int L = 2*x + 1;
int r = 2*x + 2;
if (L < n && arr[L] > arr[largest])
largest = L;
if (r < n && arr[r] > arr[largest])
largest = r;
if (largest != x)
{
int swap = arr[x];
arr[x] = arr[largest];
arr[largest] = swap;
heapify(arr, n, largest);
}
}
static void printArray(int arr[])
{
int n = arr.length;
for (int x=0; x<n; ++x)
System.out.print(arr[x]+" ");
System.out.println();
}
public static void main(String args[])
{
int arr[] = {6,1,8,3,5,2,4};
int n = arr.length;
System.out.println("Before Sorting:");
printArray(arr);
HeapSort ob = new HeapSort();
ob.sort(arr);
System.out.println("After Heap Sorting:");
printArray(arr);
}
}

Output:



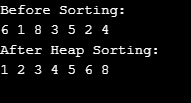
You can view it from point to level of the graph, from left to right. We achieved here that when we have the kth component in the array, the position of its children is 2\*k+1 and 2\*k+2 (assuming that indexing begins at 0). You can monitor this. The position of the parent is always (k-1)/2 for the kth component. You can readily “max heap up” any range because you know that. Check whether one of its kids is lower than that for each component. If so, pair one parent and repeat this step recursively with the parent.

Note: Since iterating for-loops across the entire array makes heapSort) (obviously O(N), it would create Heapsort O’s overall complexity(nlog n). Heapsort has an on-the-spot type, which means that it requires O(1) more room than Merge Sort, but it has some disadvantages, such as parallels that are hard.

Conclusion – Sorting Algorithms in Java

Sorting is a very prevalent procedure with datasets, whether for further analysis, speeding search with more effective algorithms relying on sorted information, filtering information, etc. Several languages endorse sorting, and often the interfaces obscure what the programmer does.

以上是Java 中的排序算法的详细内容。更多信息请关注PHP中文网其他相关文章！