Java中的递归被定义为“一个方法直接或间接地连续调用自身(同一个方法)”。递归函数用于需要一次又一次执行同一组操作直到得出结果的情况。它执行多次迭代,并且每次迭代问题陈述都变得越来越简单。 java中的递归是一种基于同一问题的较小块的解来解决问题的方法。大多数无限可能的迭代都可以通过递归来解决。我们可以说递归是循环语句的另一种方法。如果我们没有正确使用递归函数,那么它会执行无限次。
语法:
广告 该类别中的热门课程 JAVA 掌握 - 专业化 | 78 课程系列 | 15 次模拟测试returntype methodName()
{
//logic for application
methodName();//recursive call
}要停止无限条件,我们必须满足以下条件:
我们可以通过两种方式调用递归函数:
如果我们从内部方法体调用相同的方法。
语法:
returntype methodName()
{
//logic for application
methodName();//recursive call
}示例:
数字的阶乘是直接递归的一个例子。递归的基本原理是通过将复杂问题分解为更小的问题来解决它。例如,对于一个数字的阶乘,如果我们知道“i-1”的阶乘,我们就可以计算“i”的阶乘。
代码:
public class Factorial {
static int fact(int i){
if (i == 1)
return 1;
else
return(i * fact(i-1));
}
public static void main(String[] args) {
System.out.println("The factorial of given number 6 is: "+fact(6));
}
}输出:

如果我们从另一个方法调用一个方法,并且从第一个方法调用另一个方法,反之亦然。
语法:
<firstIndirectRecursive()
{
// Logic
secondIndirectRecursive();
}
secondIndirectRecursive()
{
//Logic
firstIndirectRecursive();
}示例:
为了显示间接递归,我们使用以下程序来根据给定的输入找出给定的数字是偶数还是奇数。
代码:
import java.util.Scanner;
public class IndirectRecursion {
public static boolean oddNum(int i) {
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0){
return false;
} else {
return evenNum(i-1);
}
}
public static boolean evenNum(int i) {
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0){
return true;
} else {
return oddNum(i-1);
}
}
public static void main(String[] args) {
Scanner inputNum = new Scanner(System.in);
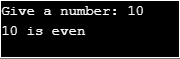
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
}
}输出:
这里还有一些使用递归方法解决问题的示例。
如果 number3=number1+number2,即每个数字都是其前两个数字之和,则称一组“n”个数字位于斐波那契数列中。因此,序列总是从前两位数字开始,如 0 和 1。第三个数字是 0 和 1 的和,结果是 1,第四个数字是 1 和 1 相加,结果是 2,序列继续。
查看以下 Java 代码来生成斐波那契数列:
代码:
public class FibonacciSeries{
static int num1=0,num2=1,num3=0;
static void fibonacci(int n){
if(n>0){
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
}
}
public static void main(String args[]){
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
}
}输出:

这里前两个数字被初始化为 0 和 1 并打印。变量“num1”、“num2”和“num3”用于生成所需的序列。变量“num3”是“num1”和“num2”相加得到的,数字通过打乱的方式向左移动一位,如代码所示。这里递归调用函数“Fibonacci”,每次迭代时,“n”的值减 1。因此,一旦“n”达到值 0,递归就会退出。
这是一个经典的数学问题,有 3 个极点和“n”个不同大小的圆盘。谜题如下:
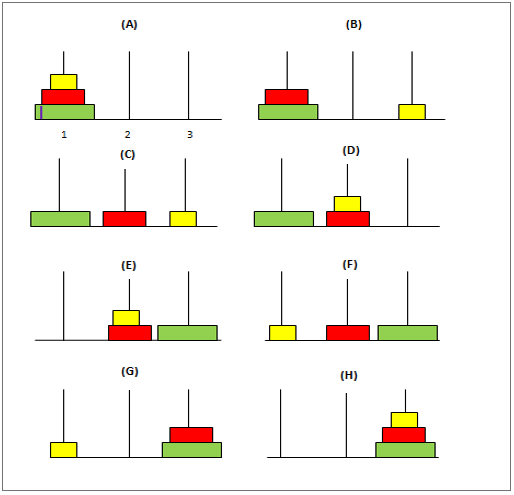
一开始,第一个杆子的圆盘排列方式是最大的圆盘位于杆的底部,最小的圆盘位于杆的顶部。目标是将这些圆盘从第一个极移动到第三个极,使圆盘保持与第一个极相同的位置。以下是移动这些磁盘时需要记住的一些条件:
以下是可用于解决该难题的Java代码:
代码:
public class TowerOfHanoi {
public static void main(String[] args) {
int count = 3;
tower(count, 'A', 'B', 'C');
}
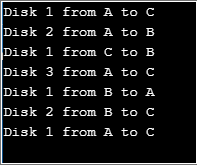
public static void tower(int first, char disk1, char temp, char disk2) {
if (first == 1) {
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
} else {
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
}
}
}输出:
Here the variable “count” represents the number of discs to be used. The function “tower” is the recursive function used to move the discs from rod 1 to rod 3. A simple solution to this problem can be provided by considering 2 discs at first.
This same principle is applied for the “n” number of discs by moving (n-1)the disc from rod 1 to 2 and following similar steps as above.
Code:
package com.recursion;
import java.util.Scanner;
public class FactorialOfNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
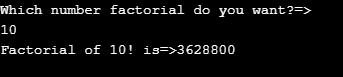
System.out.println("Which number factorial do you want?=>");
//taking input from the user
int input = scanner.nextInt();
System.out.println("Factorial of " + input + "! is=>"+getMyFactorialNumber(input));
scanner.close();
}
public static long getMyFactorialNumber(int inputNumber) {
if (inputNumber == 1)//base condition
return 1;
return inputNumber * getMyFactorialNumber(inputNumber - 1);//recursive call
}
}Output:
Code:
import java.util.Scanner;
//ARMSTRONG number means sum of numbers of cubes equal to the number
public class ArmstrongNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter any Number?=>");
// taking input from the user
int input = scanner.nextInt();
//calling isArmstrongNumber() method and put in a variable
double checkNumber=isArmstrongNumber(input);
//checking the number
if(input==checkNumber)
{
System.out.println(input+" is ARMSTRONG NUMBER");
}
else
{
System.out.println(input+" not is ARMSTRONG NUMBER");
}
scanner.close();
}
static int remainderNumber;
static double total = 0;
public static double isArmstrongNumber(int inputNumber) {
if (inputNumber > 0) {
remainderNumber = inputNumber % 10;//separating digits
total = total + Math.pow(remainderNumber, 3);//cubes sum
isArmstrongNumber(inputNumber / 10);//recursive call
}
return total;
}
}Output:
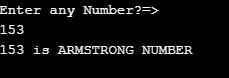
Code:
import java.util.Scanner;
public class PalindromeNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter any Number=>");
// taking input from the user
int input = scanner.nextInt();
int checkNumber = palindromeNumberOrNot(input,0);
if (checkNumber == input)
{
System.out.println(input+" is a PALINDROME NUMBER");
}
else
{
System.out.println(input+" is not a PALINDROME NUMBER");
}
scanner.close();
}
public static int palindromeNumberOrNot(int inputNumber,int baseNumber) {
if (inputNumber == 0)// base case
return baseNumber;
baseNumber = (baseNumber * 10) + (inputNumber % 10);// getting the reverse of the number and stores in temp
return palindromeNumberOrNot(inputNumber/10,baseNumber);//recursive call
}
}Output:
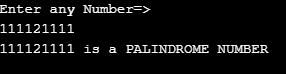
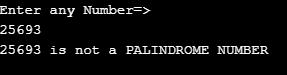
Recursive functions are relatively simpler to code, but they are also not that efficient as compared to the other existing methods. Hence they are majorly used in cases where the time given for development is less and also where a significant pattern can be observed in the problem.
以上是Java 中的递归的详细内容。更多信息请关注PHP中文网其他相关文章!




