AVL树也称为自平衡二叉树,用于平衡计算左右子树各自的高度差,其结果在整个平衡树中不能多于一个。二叉搜索树操作允许插入、删除、搜索、最大和最小操作,这也是 AVL 树的一部分所必需的。所有这些操作都被认为是成本高昂的事务,因此,如果保持所有 BST 高度之间的差异,则可以保持与其相关的成本和时间复杂度。
开始您的免费软件开发课程
网络开发、编程语言、软件测试及其他
语法:
没有这样正确的语法,但在 Java AVL 树中实现它时,它被视为一种数据结构,其语法表示如下:
Class Node_demo
{
int key, height_0;
Node left, right;
Node_demo (int d_1)
{
key = d_1;
height_0 = 1;
}
}
class AVLTree_demo1 {
Node root_0;
int height_0(Node N_1) {
if (N_1== null)
return 0;
return N_1.height;
}说明:
在此处的语法流程中,Node_demo 类包含键、高度和结构,它们描述了存储元素的键值对。接下来是包含根节点及其关联元素的 AVL_Tree demo_1 节点,其具有值对的值对,其高度在任何地方都需要维护,值为空。
其中 D 代表高度和平衡因子不为 -1、1 和 0 的节点,因此所有这些旋转都需要使它们的格式正确。
存在许多操作,为此,必须有适当的旋转和适当的操作分析。
示例:此示例演示了 AVL 树,其中插入、左插入和右插入具有前序、后序和级别顺序表示,如下面的输出所示。
import java. util.LinkedList;
import java.util.Queue;
class Node_8 {
int data_0, height_1;
Node_8 left_nd_0;
Node_8 right_nd_0;
Node_8(int d_2) {
data_0 = d_2;
height_1 = 1;
}
}
public class AVLTree_Demo
{
Node_8 root_0;
int height_1(Node_8 N) {
if (N == null)
return 0;
return N.height_1;
}
int max_2(int a_0, int b_0) {
return (a_0 > b_0) ? a_0 : b_0;
}
Node_8 rightRotation_mode(Node_8 oldRoot_0) {
Node_8 newRoot_0 = oldRoot_0.left_nd_0;
Node_8 temp_0 = newRoot_0.right_nd_0;
newRoot_0.right_nd_0 = oldRoot_0;
oldRoot_0.left_nd_0 = temp_0;
newRoot_0.height_1 = max_2(height_1(newRoot_0.left_nd_0), height_1(newRoot_0.right_nd_0)) + 1;
oldRoot_0.height_1 = max_2(height_1(oldRoot_0.left_nd_0), height_1(oldRoot_0.right_nd_0)) + 1;
return newRoot_0;
}
Node_8 leftRotation_mode(Node_8 oldRoot_0) {
Node_8 newRoot_0 = oldRoot_0.right_nd_0;
Node_8 temp_0 = newRoot_0.left_nd_0;
newRoot_0.left_nd_0 = oldRoot_0;
oldRoot_0.right_nd_0 = temp_0;
newRoot_0.height_1 = max_2(height_1(newRoot_0.left_nd_0), height_1(newRoot_0.right_nd_0)) + 1;
oldRoot_0.height_1=max_2(height_1(oldRoot_0.left_nd_0), height_1(oldRoot_0.right_nd_0)) + 1;
return newRoot_0;
}
int balFactor_c(Node_8 root_0) {
if(root_0 == null)
return 0;
return height_1(root_0.left_nd_0) - height_1(root_0.right_nd_0);
}
Node_8 insert(Node_8 root_0, int data_0) {
if(root_0 == null)
return new Node_8(data_0);
else if(data_0 < root_0.data_0)
root_0.left_nd_0 = insert(root_0.left_nd_0, data_0);
else if(data_0 > root_0.data_0)
root_0.right_nd_0 = insert(root_0.right_nd_0, data_0);
else
return root_0;
root_0.height_1= max_2(height_1(root_0.left_nd_0), height_1(root_0.right_nd_0)) + 1;
int bal = balFactor_c(root_0);
if(bal > 1 && data_0 < root_0.left_nd_0.data_0)
return rightRotation_mode(root_0);
if(bal < -1 && data_0 > root_0.right_nd_0.data_0)
return leftRotation_mode(root_0);
if(bal > 1 && data_0 > root_0.left_nd_0.data_0) {
root_0.left_nd_0 = leftRotation_mode(root_0.left_nd_0);
return rightRotation_mode(root_0);
}
if(bal < -1 && data_0 < root_0.right_nd_0.data_0) {
root_0.right_nd_0 = rightRotation_mode(root_0.right_nd_0);
return leftRotation_mode(root_0);
}
return root_0;
}
void preOrder_traversal(Node_8 node) {
if (node != null) {
System.out.print(node.data_0 + " ");
preOrder_traversal(node.left_nd_0);
preOrder_traversal(node.right_nd_0);
}
}
void levelOrder_traversal(Node_8 root) {
Queue<Node_8> q_1 = new LinkedList<Node_8>();
q_1.add(root);
while(!q_1.isEmpty()) {
Node_8 current = q_1.peek();
System.out.print(current.data_0 + " ");
if(current.left_nd_0 != null)
q_1.add(current.left_nd_0);
if(current.right_nd_0 != null)
q_1.add(current.right_nd_0);
q_1.poll();
}
}
public static void main (String args[]) {
AVLTree_Demo tree = new AVLTree_Demo ();
tree. root_0 = tree.insert(tree.root_0, 15);
tree.root_0 = tree.insert(tree.root_0, 20);
tree.root_0 = tree.insert(tree.root_0, 19);
tree.root_0 = tree.insert(tree.root_0, 40);
tree.root_0 = tree.insert(tree.root_0, 50);
tree.root_0 = tree.insert(tree.root_0, 25);
System.out.println("order_of_Preorder_traversal_representation : ");
tree.preOrder_traversal(tree.root_0);
System.out.println();
System.out.println("Levelorder_of_traversal_representation : ");
tree.levelOrder_traversal(tree.root_0);
}
}输出:
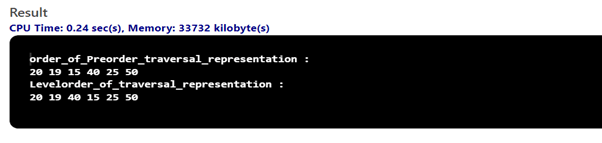
说明:该程序在 AVL 树中执行插入元素操作,其中存在某种顺序,其中一些检查例如所采用的列表是否为空,然后 AVL 树是否有以预序、后序或级别顺序格式执行轮换。所有给出的元素都会自动接受输入并按正确的顺序排列它们。
Java 中的 AVL 树被用作一种合适的数据结构,受到许多开发人员的喜爱,因为它在操作方面具有优势,并且有助于节省和消耗由大量代码创建的时间复杂度。如果高度保持得当,AVL 树有能力处理整个子树的插入、删除、旋转和移除等主要操作。
以上是AVL树java的详细内容。更多信息请关注PHP中文网其他相关文章!




