加权图类-java教程-PHP中文网

首页

Java

java教程

加权图类

WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWB

Sep 06, 2024 am 06:01 AM

WeightedGraph 类扩展了 AbstractGraph。
前面的章节设计了用于对图进行建模的 Graph 接口、AbstractGraph 类和 UnweightedGraph 类。按照这种模式，我们将 WeightedGraph 设计为 AbstractGraph 的子类，如下图所示。

The WeightedGraph Class

WeightedGraph 只需使用五个构造函数扩展 AbstractGraph 即可创建具体的 WeightedGraph 实例。 WeightedGraph 继承了 AbstractGraph 的所有方法，重写了 clear 和 addVertex 方法，实现了新的 addEdge 方法添加加权边，还引入了获取最小生成树和查找所有单源最短路径的新方法。最小生成树和最短路径将在最小生成树和最短路径部分分别介绍。

下面的代码实现了WeightedGraph。边邻接列表（第 38-63 行）在内部用于存储顶点的相邻边。当构造 WeightedGraph 时，会创建它的边邻接列表（第 47 和 57 行）。方法 getMinimumSpanningTree()（第 99-138 行）和 getShortestPath()（第 156-197 行）将在接下来的部分中介绍。

package demo;
import java.util.*;

public class WeightedGraph<V> extends AbstractGraph<V> {
    /** Construct an empty */
    public WeightedGraph() {}

    /** Construct a WeightedGraph from vertices and edged in arrays */
    public WeightedGraph(V[] vertices, int[][] edges) {
        createWeightedGraph(java.util.Arrays.asList(vertices), edges);
    }

     /** Construct a WeightedGraph from vertices and edges in list */
    public WeightedGraph(int[][] edges, int numberOfVertices) {
        List<V> vertices = new ArrayList<>();
        for (int i = 0; i < numberOfVertices; i++)
            vertices.add((V)(new Integer(i)));

        createWeightedGraph(vertices, edges);
    }

    /** Construct a WeightedGraph for vertices 0, 1, 2 and edge list */
    public WeightedGraph(List<V> vertices, List<WeightedEdge> edges) {
        createWeightedGraph(vertices, edges);
    }

    /** Construct a WeightedGraph from vertices 0, 1, and edge array */
    public WeightedGraph(List<WeightedEdge> edges, int numberOfVertices) {
        List<V> vertices = new ArrayList<>();
        for (int i = 0; i < numberOfVertices; i++)
            vertices.add((V)(new Integer(i)));

        createWeightedGraph(vertices, edges);
    }

    /** Create adjacency lists from edge arrays */
    private void createWeightedGraph(List<V> vertices, int[][] edges) {
        this.vertices = vertices;

        for (int i = 0; i < vertices.size(); i++) {
            neighbors.add(new ArrayList<Edge>()); // Create a list for vertices
        }

        for (int i = 0; i < edges.length; i++) {
            neighbors.get(edges[i][0]).add(new WeightedEdge(edges[i][0], edges[i][1], edges[i][2]));
        }
    }

    /** Create adjacency lists from edge lists */
    private void createWeightedGraph(List<V> vertices, List<WeightedEdge> edges) {
        this.vertices = vertices;

        for (int i = 0; i < vertices.size(); i++) {
            neighbors.add(new ArrayList<Edge>()); // Create a list for vertices
        }

        for (WeightedEdge edge: edges) {
            neighbors.get(edge.u).add(edge); // Add an edge into the list
        }
    }

    /** Return the weight on the edge (u, v) */
    public double getWeight(int u, int v) throws Exception {
        for (Edge edge : neighbors.get(u)) {
            if (edge.v == v) {
                return ((WeightedEdge)edge).weight;
            }
        }

        throw new Exception("Edge does not exit");
    }

    /** Display edges with weights */
    public void printWeightedEdges() {
        for (int i = 0; i < getSize(); i++) {
            System.out.print(getVertex(i) + " (" + i + "): ");
            for (Edge edge : neighbors.get(i)) {
                System.out.print("(" + edge.u + ", " + edge.v + ", " + ((WeightedEdge)edge).weight + ") ");
            }

            System.out.println();
        }
    }

    /** Add edges to the weighted graph */
    public boolean addEdge(int u, int v, double weight) {
        return addEdge(new WeightedEdge(u, v, weight));
    }

    /** Get a minimum spanning tree rooted at vertex 0 */
    public MST getMinimumSpanningTree() {
        return getMinimumSpanningTree(0);
    }

    /** Get a minimum spanning tree rooted at a specified vertex */
    public MST getMinimumSpanningTree(int startingVertex) {
        // cost[v] stores the cost by adding v to the tree
        double[] cost = new double[getSize()];
        for (int i = 0; i < cost.length; i++) {
            cost[i] = Double.POSITIVE_INFINITY; // Initial cost
        }
        cost[startingVertex] = 0; // Cost of source is 0

        int[] parent = new int[getSize()]; // Parent of a vertex
        parent[startingVertex] = -1; // startingVertex is the root
        double totalWeight = 0; // Total weight of the tree thus far

        List<Integer> T = new ArrayList<>();

        // Expand T
        while (T.size() < getSize()) {
            // Find smallest cost v in V - T
            int u = -1; // Vertex to be determined
            double currentMinCost = Double.POSITIVE_INFINITY;
            for (int i = 0; i < getSize(); i++) {
                if (!T.contains(i) && cost[i] < currentMinCost) {
                    currentMinCost = cost[i];
                    u = i;
                }
            }

            T.add(u); // Add a new vertex to T
            totalWeight += cost[u]; // Add cost[u] to the tree

            // Adjust cost[v] for v that is adjacent to u and v in V - T
            for (Edge e : neighbors.get(u)) {
                if (!T.contains(e.v) && cost[e.v] > ((WeightedEdge)e).weight) {
                    cost[e.v] = ((WeightedEdge)e).weight;
                    parent[e.v] = u;
                }
            }
        } // End of while

        return new MST(startingVertex, parent, T, totalWeight);
    }

    /** MST is an inner class in WeightedGraph */
    public class MST extends Tree {
        private double totalWeight; // Total weight of all edges in the tree

        public MST(int root, int[] parent, List<Integer> searchOrder, double totalWeight) {
            super(root, parent, searchOrder);
            this.totalWeight = totalWeight;
        }

        public double getTotalWeight() {
            return totalWeight;
        }
    }

    /** Find single source shortest paths */
    public ShortestPathTree getShortestPath(int sourceVertex) {
        // cost[v] stores the cost of the path from v to the source
        double[] cost = new double[getSize()];
        for (int i = 0; i < cost.length; i++) {
            cost[i] = Double.POSITIVE_INFINITY; // Initial cost set to infinity
        }
        cost[sourceVertex] = 0; // Cost of source is 0

        // parent[v] stores the previous vertex of v in the path
        int[] parent = new int[getSize()];
        parent[sourceVertex] = -1; // The parent of source is set to -1

        // T stores the vertices whose path found so far
        List<Integer> T = new ArrayList<>();

        // Expand T
        while (T.size() < getSize()) {
            // Find smallest cost v in V - T
            int u = -1; // Vertex to be determined
            double currentMinCost = Double.POSITIVE_INFINITY;
            for (int i = 0; i < getSize(); i++) {
                if (!T.contains(i) && cost[i] < currentMinCost) {
                    currentMinCost = cost[i];
                    u = i;
                }
            }

            T.add(u); // Add a new vertex to T

            // Adjust cost[v] for v that is adjacent to u and v in V - T
            for (Edge e : neighbors.get(u)) {
                if (!T.contains(e.v) && cost[e.v] > cost[u] + ((WeightedEdge)e).weight) {
                    cost[e.v] = cost[u] + ((WeightedEdge)e).weight;
                    parent[e.v] = u;
                }
            }
        } // End of while

        // Create a ShortestPathTree
        return new ShortestPathTree(sourceVertex, parent, T, cost);
    }

    /** ShortestPathTree is an inner class in WeightedGraph */
    public class ShortestPathTree extends Tree {
        private double[] cost; // cost[v] is the cost from v to source

        /** Construct a path */
        public ShortestPathTree(int source, int[] parent, List<Integer> searchOrder, double[] cost) {
            super(source, parent, searchOrder);
            this.cost = cost;
        }

        /** Return the cost for a path from the root to vertex v */
        public double getCost(int v) {
            return cost[v];
        }

        /** Print paths from all vertices to the source */
        public void printAllPaths() {
            System.out.println("All shortest paths from " + vertices.get(getRoot()) + " are:");
            for (int i = 0; i < cost.length; i++) {
                printPath(i); // Print a path from i to the source
                System.out.println("(cost: " + cost[i] + ")"); // Path cost
            }
        }
    }
}

登录后复制

WeightedGraph 类扩展了 AbstractGraph 类（第 3 行）。 AbstractGraph 中的属性 vertices 和 neighbors 继承于 WeightedGraph.neighbors 是一个列表。列表中的每个元素都是另一个包含边的列表。对于未加权图，每条边都是 AbstractGraph.Edge 的实例。对于加权图，每条边都是 WeightedEdge 的实例。 WeightedEdge 是 Edge 的子类型。因此，您可以将加权边添加到 neighbors.get(i) 中以获得加权图（第 47 行）。

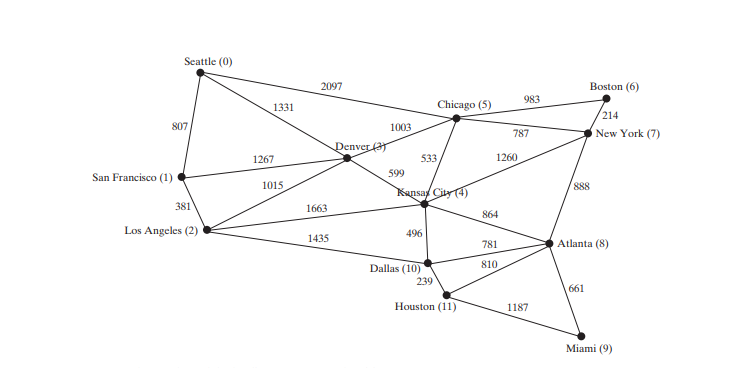
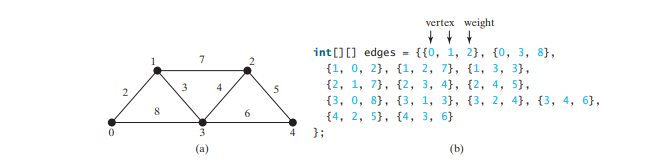
下面的代码给出了一个测试程序，该程序为下图中的图创建一个图，并为下图a中的图创建另一个图。

The WeightedGraph Class

package demo;

public class TestWeightedGraph {

    public static void main(String[] args) {
        String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1, 807}, {0, 3, 1331}, {0, 5, 2097},
                {1, 0, 807}, {1, 2, 381}, {1, 3, 1267},
                {2, 1, 381}, {2, 3, 1015}, {2, 4, 1663}, {2, 10, 1435},
                {3, 0, 1331}, {3, 1, 1267}, {3, 2, 1015}, {3, 4, 599}, {3, 5, 1003},
                {4, 2, 1663}, {4, 3, 599}, {4, 5, 533}, {4, 7, 1260}, {4, 8, 864}, {4, 10, 496},
                {5, 0, 2097}, {5, 3, 1003}, {5, 4, 533}, {5, 6, 983}, {5, 7, 787},
                {6, 5, 983}, {6, 7, 214},
                {7, 4, 1260}, {7, 5, 787}, {7, 6, 214}, {7, 8, 888},
                {8, 4, 864}, {8, 7, 888}, {8, 9, 661}, {8, 10, 781}, {8, 11, 810},
                {9, 8, 661}, {9, 11, 1187},
                {10, 2, 1435}, {10, 4, 496}, {10, 8, 781}, {10, 11, 239},
                {11, 8, 810}, {11, 9, 1187}, {11, 10, 239}
        };

        WeightedGraph<String> graph1 = new WeightedGraph<>(vertices, edges);
        System.out.println("The number of vertices in graph1: " + graph1.getSize());
        System.out.println("The vertex with index 1 is " + graph1.getVertex(1));
        System.out.println("The index for Miami is " + graph1.getIndex("Miami"));
        System.out.println("The edges for graph1:");
        graph1.printWeightedEdges();

        edges = new int[][] {
            {0, 1, 2}, {0, 3, 8},
            {1, 0, 2}, {1, 2, 7}, {1, 3, 3},
            {2, 1, 7}, {2, 3, 4}, {2, 4, 5},
            {3, 0, 8}, {3, 1, 3}, {3, 2, 4}, {3, 4, 6},
            {4, 2, 5}, {4, 3, 6}
        };
        WeightedGraph<Integer> graph2 = new WeightedGraph<>(edges, 5);
        System.out.println("\nThe edges for graph2:");
        graph2.printWeightedEdges();
    }
}

登录后复制

graph1 中的顶点数量：12
索引为 1 的顶点是旧金山
迈阿密的指数是 9
graph1 的边：
顶点 0: (0, 1, 807) (0, 3, 1331) (0, 5, 2097)
顶点 1: (1, 2, 381) (1, 0, 807) (1, 3, 1267)
顶点 2： (2, 1, 381) (2, 3, 1015) (2, 4, 1663) (2, 10, 1435)
顶点 3: (3, 4, 599) (3, 5, 1003) (3, 1, 1267)
(3, 0, 1331) (3, 2, 1015)
顶点 4： (4, 10, 496) (4, 8, 864) (4, 5, 533) (4, 2, 1663)
(4, 7, 1260) (4, 3, 599)
顶点 5: (5, 4, 533) (5, 7, 787) (5, 3, 1003)
(5, 0, 2097) (5, 6, 983)
顶点 6: (6, 7, 214) (6, 5, 983)
顶点 7: (7, 6, 214) (7, 8, 888) (7, 5, 787) (7, 4, 1260)
顶点 8: (8, 9, 661) (8, 10, 781) (8, 4, 864)
(8, 7, 888) (8, 11, 810)
顶点 9: (9, 8, 661) (9, 11, 1187)
顶点 10： (10, 11, 239) (10, 4, 496) (10, 8, 781) (10, 2, 1435)
顶点 11： (11, 10, 239) (11, 9, 1187) (11, 8, 810)

graph2 的边：
顶点 0: (0, 1, 2) (0, 3, 8)
顶点 1: (1, 0, 2) (1, 2, 7) (1, 3, 3)
顶点 2: (2, 3, 4) (2, 1, 7) (2, 4, 5)
顶点 3： (3, 1, 3) (3, 4, 6) (3, 2, 4) (3, 0, 8)
顶点 4: (4, 2, 5) (4, 3, 6)

程序为上图中第 3-27 行的图表创建 graph1。 graph1 的顶点在第 3-5 行中定义。 graph1 的边在第 7-24 行中定义。边缘使用二维数组表示。对于数组中的每一行 i，edges[i][0] 和 edges[i][1] 表示从顶点 edges[i] 有一条边[0] 到顶点 edges[i][1]，边的权重为 edges[i][2]。例如，{0, 1, 807}（第 8 行）表示来自顶点 0 的边 (edges[ 0][0]) 到顶点 1 (边[0][1])，权重 807 (边[0] [2]）。 {0, 5, 2097}（第 8 行）表示从顶点 0 开始的边 (edges[2][ 0]) 到顶点 5 (边[2][1])，权重 2097 (边[2][2] ）。第 35 行调用 graph1 上的 printWeightedEdges() 方法来显示 graph1 中的所有边。