我上一篇博文的一位读者向我指出,对于切片 matmul 之类的操作,np.einsum 比 np.matmul 慢得多,除非您在参数列表中打开优化标志: np.einsum(.. ., 优化 = True).
带着一些怀疑,我启动了 Jupyter 笔记本并做了一些初步测试。 我天哪,这是完全正确的 - 即使对于两个操作数的情况,优化根本不应该产生任何区别!
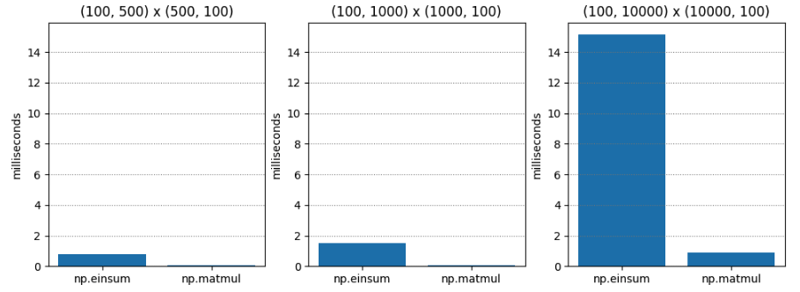
测试 1 非常简单 - 两个不同维度的 C 阶(又名行主阶)矩阵的矩阵乘法。 np.matmul 始终快二十倍左右。
| M1 | M2 | np.einsum | np.matmul | np.einsum / np.matmul |
|---|---|---|---|---|
| (100, 500) | (500, 100) | 0.765 | 0.045 | 17.055 |
| (100, 1000) | (1000, 100) | 1.495 | 0.073 | 20.554 |
| (100, 10000) | (10000, 100) | 15.148 | 0.896 | 16.899 |
对于测试2,当optimize=True时,结果截然不同。 np.einsum 仍然较慢,但最坏情况下也仅慢 1.5 倍左右!

| M1 | M2 | np.einsum | np.matmul | np.einsum / np.matmul |
|---|---|---|---|---|
| (100, 500) | (500, 100) | 0.063 | 0.043 | 1.474 |
| (100, 1000) | (1000, 100) | 0.086 | 0.067 | 1.284 |
| (100, 10000) | (10000, 100) | 1.000 | 0.936 | 1.068 |
我对优化标志的理解是,当存在三个或更多操作数时,它确定最佳收缩顺序。 这里,我们只有两个操作数。 所以优化应该不会有什么不同,对吧?
但也许优化不仅仅只是选择收缩顺序? 也许优化器知道内存布局,这与行优先与列优先布局有关?
在矩阵乘法的小学方法中,要计算单个条目,您将迭代 op1 中的行,同时迭代 op2 中的列,因此将第二个参数按列优先顺序放置可能会导致加速对于 np.einsum (假设 np.einsum 有点像底层矩阵乘法的小学方法的通用版本,我怀疑这是真的)。
因此,对于 测试 3,我为第二个操作数传递了一个列主矩阵,以查看当 optimize=False 时这是否会加快 np.einsum 的速度。
这是结果。 令人惊讶的是,np.einsum 仍然相当更糟。 显然,发生了一些我不明白的事情 - 当 optimize 为 True 时,也许 np.einsum 使用完全不同的代码路径? 是时候开始挖掘了。

| M1 | M2 | np.einsum | np.matmul | np.einsum / np.matmul |
|---|---|---|---|---|
| (100, 500) | (500, 100) | 1.486 | 0.056 | 26.541 |
| (100, 1000) | (1000, 100) | 3.885 | 0.125 | 31.070 |
| (100, 10000) | (10000, 100) | 49.669 | 1.047 | 47.444 |
Numpy 1.12.0 的发行说明提到了优化标志的引入。 然而,优化的目的似乎是确定操作数链中参数的组合顺序(即关联性) - 因此优化不应仅对两个操作数产生影响,对吧? 以下是发行说明:
np.einsum 现在支持优化参数,它将优化收缩顺序。例如,np.einsum 将在一次传递中完成链点示例 np.einsum(‘ij,jk,kl->il’, a, b, c),其缩放比例类似于 N^4;然而,当optimize=True时,np.einsum将创建一个中间数组,以将这种缩放减少到N^3或有效地np.dot(a, b).dot(c)。使用中间张量来减少缩放已应用于通用 einsum 求和符号。有关更多详细信息,请参阅 np.einsum_path。
为了让这个谜团更加复杂,一些后来的发行说明表明 np.einsum 已升级为使用tensordot(它本身在适当的情况下使用BLAS)。 现在,这似乎很有希望。
但是,为什么我们仅在优化为True时看到加速? 发生什么事了?
如果我们在 numpy/numpy/_core/einsumfunc.py 中阅读 def einsum(*operands, out=None, optimization=False, **kwargs) ,我们几乎会立即看到这个提前退出的逻辑:
# If no optimization, run pure einsum
if optimize is False:
if specified_out:
kwargs['out'] = out
return c_einsum(*operands, **kwargs)
c_einsum 是否使用tensordot? 我对此表示怀疑。 稍后在代码中,我们看到 1.14 注释似乎引用了 tensordot 调用:
# Start contraction loop
for num, contraction in enumerate(contraction_list):
...
# Call tensordot if still possible
if blas:
...
# Contract!
new_view = tensordot(
*tmp_operands, axes=(tuple(left_pos), tuple(right_pos))
)
所以,这就是发生的事情:
对我来说,这似乎是一个错误。 恕我直言, np.einsum 开头的“提前退出”仍应检测操作数是否与tensordot兼容,并在可能的情况下调用tensordot。 然后,即使优化为 False,我们也会得到明显的 BLAS 加速。 毕竟,优化的语义与收缩顺序有关,而不是与 BLAS 的使用有关,我认为这应该是给定的。
这里的好处是,调用 np.einsum 进行相当于张量调用的操作的人将获得适当的加速,从性能角度来看,这使得 np.einsum 的危险性降低了一些。
我深入研究了一些 C 代码来检查它。 实现的核心就在这里。
经过大量的参数解析和参数准备,确定了轴迭代顺序并准备了专用迭代器。 迭代器的每个收益都代表了同时跨过所有操作数的不同方式。
# If no optimization, run pure einsum
if optimize is False:
if specified_out:
kwargs['out'] = out
return c_einsum(*operands, **kwargs)
假设某些特殊情况优化不适用,则根据涉及的数据类型确定适当的乘积和 (sop) 函数:
# Start contraction loop
for num, contraction in enumerate(contraction_list):
...
# Call tensordot if still possible
if blas:
...
# Contract!
new_view = tensordot(
*tmp_operands, axes=(tuple(left_pos), tuple(right_pos))
)
然后,在从迭代器返回的每个多操作数步幅上调用此乘积和 (sop) 运算,如下所示:
/* Allocate the iterator */
iter = NpyIter_AdvancedNew(nop+1, op, iter_flags, order, casting, op_flags,
op_dtypes, ndim_iter, op_axes, NULL, 0);
这就是我对 einsum 工作原理的理解,诚然,它仍然有点薄弱——它确实值得我花更多的时间来了解它。
但它确实证实了我的怀疑,它的作用就像小学矩阵乘法方法的广义、千兆脑版本。 最终,它委托给一系列“乘积之和”运算,这些运算依赖于在操作数中移动的“跨步器”——与学习矩阵乘法时用手指所做的没有太大不同。
那么为什么当你使用optimize=True调用np.einsum时通常会更快呢? 原因有两个。
第一个(也是最初的)原因是它试图找到最佳的收缩路径。 然而,正如我所指出的,当我们只有两个操作数时,这应该不重要,就像我们在性能测试中所做的那样。
第二个(也是较新的)原因是,当optimize=True时,即使在两个操作数的情况下,它也会激活一个代码路径,在可能的情况下调用tensordot,而tensordot又会尝试使用BLAS。 BLAS 与矩阵乘法一样优化!
所以,双操作数加速之谜解决了! 然而,我们还没有真正涵盖由于收缩顺序而导致的加速特性。 这得等以后的帖子了! 敬请期待!
以上是研究 np.einsum 的性能的详细内容。更多信息请关注PHP中文网其他相关文章!




