合并两棵树后找到最小直径-php教程-PHP中文网

3203。合并两棵树后找到最小直径

难度：难

主题：树、深度优先搜索、广度优先搜索、图

存在两棵无向树，分别有n和m个节点，编号分别为0到n - 1和0到m - 1。给定两个二维整数数组edges1和edges2，长度分别为n - 1和m - 1，其中edges1[i] = [a_i, b_i]表示有是第一棵树中节点 a_i 和 b_i 之间的边，edges2[i] = [u_i, v_i] 表示第二棵树中的节点 u_i 和 v_i 之间有一条边。

您必须使用边将第一棵树中的一个节点与第二棵树中的另一个节点连接起来。

返回所得树的最小值可能的直径。

树的直径是树中任意两个节点之间最长路径的长度。

示例1：

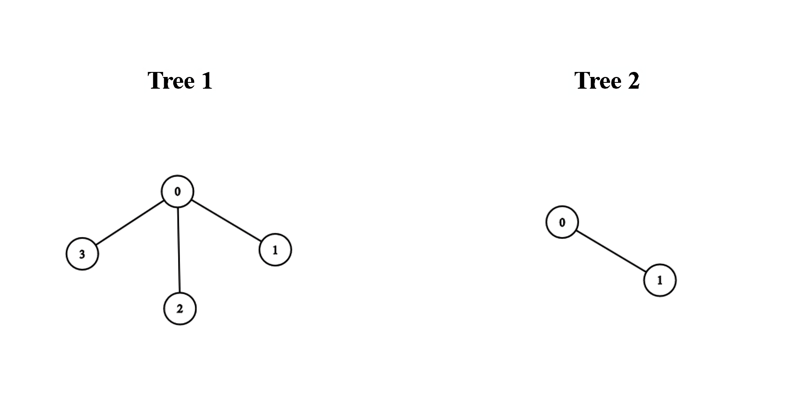
Find Minimum Diameter After Merging Two Trees

输入： Edges1 = [[0,1],[0,2],[0,3]], Edges2 = [[0,1]]
输出： 3
说明：通过将第一棵树的节点 0 与第二棵树的任意节点连接，我们可以得到一棵直径为 3 的树。

示例2：

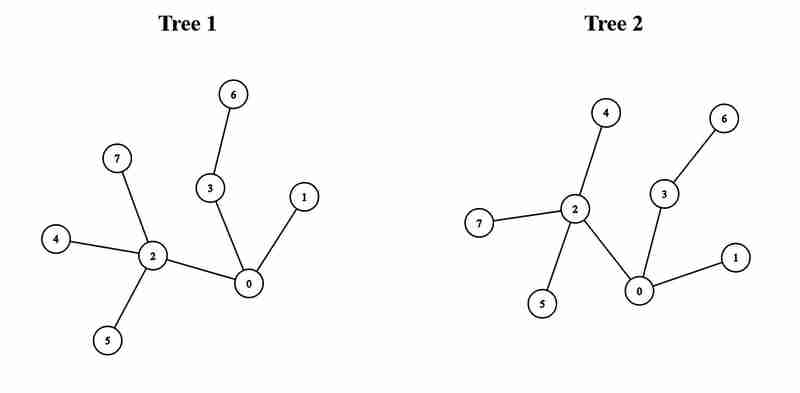
Find Minimum Diameter After Merging Two Trees

输入：edges1 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2, 7]]，边2 = [[0,1]，[0,2]，[0,3]，[2,4]，[2,5]，[3,6]，[2,7]]
输出： 5
说明：通过将第一棵树的节点 0 与第二棵树的节点 0 连接起来，我们可以得到一棵直径为 5 的树。

约束：

1 5
edges1.length == n - 1
edges2.length == m - 1
edges1[i].length == Edges2[i].length == 2
edges1[i] = [a_i, b_i]
0 i, b_i
edges2[i] = [u_i, v_i]
0 i, v_i
生成输入，使得edge1和edge2代表有效的树。

提示：

假设我们将tree1中的节点a与tree2中的节点b连接起来。生成的树的直径长度将是以下 3 个值中最大的一个：
1. 树的直径1.
2. 树的直径2.
3. 从节点 a 开始且完全在树 1 内的最长路径的长度从节点 b 开始且完全在树 2 内的最长路径的长度 1.
4. 第三个值中添加的一个是由于我们在树 1 和 2 之间添加了额外的边。
无论我们选择 a 和 b，值 1 和 2 都是恒定的。因此，我们需要以最小化值 3 的方式选择 a 和 b。
如果我们选择最佳的 a 和 b，它们将分别位于 Tree 1 和 Tree 2 的直径内。我们到底应该选择哪些直径的节点？
a 是树 1 的直径中心，b 是树 2 的直径中心。

解决方案：

我们需要逐步解决它，重点是了解如何计算树的直径以及连接两棵树如何影响总直径。

解决步骤：

求每棵树的直径:
- 树的直径是任意两个节点之间最长的路径。为了找到它，我们可以使用以下两步过程：
  1. 从任意节点执行 BFS（或 DFS）以找到最远的节点（我们将此节点称为 A）。
  2. 从A开始再进行一次BFS（或DFS），找到距离A最远的节点（我们称这个节点为B），A到B的距离就是树的直径。
确定最佳连接节点:
- 从问题的提示来看，连接两棵树时最小化附加直径的最佳方法是连接两棵树的直径中心。这将最大限度地减少新边造成的最长路径。
- 树直径中的最佳节点通常是“中心”，可以通过从直径的端点执行 BFS 并找到最长路径的中间来找到它。
最小化总直径:
- 一旦我们找到两棵树的中心，新的直径就是以下值中的最大值：
  - 树 1 的直径。
  - 树 2 的直径。
  - 树 1 中的最长路径、树 2 中的最长路径以及新连接边 1 的总和。

让我们用 PHP 实现这个解决方案：3203。合并两棵树后求最小直径

<?php
/**
 * @param Integer[][] $edges1
 * @param Integer[][] $edges2
 * @return Integer
 */
function minimumDiameterAfterMerge($edges1, $edges2) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

/**
 * Helper function to find the diameter of a tree and the farthest node from a start node
 *
 * @param $n
 * @param $edges
 * @param $start
 * @return array
 */
function bfs($n, $edges, $start) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

/**
 * Helper function to find the diameter of a tree and its center
 *
 * @param $n
 * @param $edges
 * @return array
 */
function getDiameterAndCenter($n, $edges) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example 1
$edges1 = [[0,1],[0,2],[0,3]];
$edges2 = [[0,1]];
echo minimumDiameterAfterMerge($edges1, $edges2);  // Output: 3

// Example 2
$edges1 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]];
$edges2 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]];
echo minimumDiameterAfterMerge($edges1, $edges2);  // Output: 5
?>

登录后复制

解释：

BFS 辅助函数：bfs 函数计算距离给定起始节点最远的节点，并返回距离数组和找到的最远节点。这对于计算树的直径至关重要。
获取直径和中心：getDiameterAndCenter 函数查找树的直径及其中心。合并两棵树时，树的中心对于最小化新树的直径至关重要。
主要解决方案：
- 我们首先为两棵树构建邻接表。
- 我们计算两棵树的直径和中心。
- 我们从两棵树的中心执行 BFS，以获得每棵树内的最长路径。
- 最后，我们计算三个值中的最大值，得到合并树的最小直径。