几篇关于无限分类算法的文章第1/5页_PHP教程
http://dev.mysql.com/tech-resources/articles/hierarchical-data.html
Introduction
Most users at one time or another have dealt with hierarchical data in a SQL database and no doubt learned that the management of hierarchical data is not what a relational database is intended for. The tables of a relational database are not hierarchical (like XML), but are simply a flat list. Hierarchical data has a parent-child relationship that is not naturally represented in a relational database table.
For our purposes, hierarchical data is a collection of data where each item has a single parent and zero or more children (with the exception of the root item, which has no parent). Hierarchical data can be found in a variety of database applications, including forum and mailing list threads, business organization charts, content management categories, and product categories. For our purposes we will use the following product category hierarchy from an fictional electronics store:

These categories form a hierarchy in much the same way as the other examples cited above. In this article we will examine two models for dealing with hierarchical data in MySQL, starting with the traditional adjacency list model.
The Adjacency List Model
Typically the example categories shown above will be stored in a table like the following (I'm including full CREATE and INSERT statements so you can follow along):
CREATE TABLE category( category_id INT AUTO_INCREMENT PRIMARY KEY, name VARCHAR(20) NOT NULL, parent INT DEFAULT NULL); INSERT INTO category VALUES(1,'ELECTRONICS',NULL),(2,'TELEVISIONS',1),(3,'TUBE',2), (4,'LCD',2),(5,'PLASMA',2),(6,'PORTABLE ELECTRONICS',1), (7,'MP3 PLAYERS',6),(8,'FLASH',7), (9,'CD PLAYERS',6),(10,'2 WAY RADIOS',6); SELECT * FROM category ORDER BY category_id; +-------------+----------------------+--------+ | category_id | name | parent | +-------------+----------------------+--------+ | 1 | ELECTRONICS | NULL | | 2 | TELEVISIONS | 1 | | 3 | TUBE | 2 | | 4 | LCD | 2 | | 5 | PLASMA | 2 | | 6 | PORTABLE ELECTRONICS | 1 | | 7 | MP3 PLAYERS | 6 | | 8 | FLASH | 7 | | 9 | CD PLAYERS | 6 | | 10 | 2 WAY RADIOS | 6 | +-------------+----------------------+--------+ 10 rows in set (0.00 sec)
In the adjacency list model, each item in the table contains a pointer to its parent. The topmost element, in this case electronics, has a NULL value for its parent. The adjacency list model has the advantage of being quite simple, it is easy to see that FLASH is a child of mp3 players, which is a child of portable electronics, which is a child of electronics. While the adjacency list model can be dealt with fairly easily in client-side code, working with the model can be more problematic in pure SQL.
Retrieving a Full Tree
The first common task when dealing with hierarchical data is the display of the entire tree, usually with some form of indentation. The most common way of doing this is in pure SQL is through the use of a self-join:
SELECT t1.name AS lev1, t2.name as lev2, t3.name as lev3, t4.name as lev4 FROM category AS t1 LEFT JOIN category AS t2 ON t2.parent = t1.category_id LEFT JOIN category AS t3 ON t3.parent = t2.category_id LEFT JOIN category AS t4 ON t4.parent = t3.category_id WHERE t1.name = 'ELECTRONICS'; +-------------+----------------------+--------------+-------+ | lev1 | lev2 | lev3 | lev4 | +-------------+----------------------+--------------+-------+ | ELECTRONICS | TELEVISIONS | TUBE | NULL | | ELECTRONICS | TELEVISIONS | LCD | NULL | | ELECTRONICS | TELEVISIONS | PLASMA | NULL | | ELECTRONICS | PORTABLE ELECTRONICS | MP3 PLAYERS | FLASH | | ELECTRONICS | PORTABLE ELECTRONICS | CD PLAYERS | NULL | | ELECTRONICS | PORTABLE ELECTRONICS | 2 WAY RADIOS | NULL | +-------------+----------------------+--------------+-------+ 6 rows in set (0.00 sec)
Finding all the Leaf Nodes
We can find all the leaf nodes in our tree (those with no children) by using a LEFT JOIN query:
SELECT t1.name FROM category AS t1 LEFT JOIN category as t2 ON t1.category_id = t2.parent WHERE t2.category_id IS NULL; +--------------+ | name | +--------------+ | TUBE | | LCD | | PLASMA | | FLASH | | CD PLAYERS | | 2 WAY RADIOS | +--------------+
Retrieving a Single Path
The self-join also allows us to see the full path through our hierarchies:
SELECT t1.name AS lev1, t2.name as lev2, t3.name as lev3, t4.name as lev4 FROM category AS t1 LEFT JOIN category AS t2 ON t2.parent = t1.category_id LEFT JOIN category AS t3 ON t3.parent = t2.category_id LEFT JOIN category AS t4 ON t4.parent = t3.category_id WHERE t1.name = 'ELECTRONICS' AND t4.name = 'FLASH'; +-------------+----------------------+-------------+-------+ | lev1 | lev2 | lev3 | lev4 | +-------------+----------------------+-------------+-------+ | ELECTRONICS | PORTABLE ELECTRONICS | MP3 PLAYERS | FLASH | +-------------+----------------------+-------------+-------+ 1 row in set (0.01 sec)
The main limitation of such an approach is that you need one self-join for every level in the hierarchy, and performance will naturally degrade with each level added as the joining grows in complexity.
Limitations of the Adjacency List Model
Working with the adjacency list model in pure SQL can be difficult at best. Before being able to see the full path of a category we have to know the level at which it resides. In addition, special care must be taken when deleting nodes because of the potential for orphaning an entire sub-tree in the process (delete the portable electronics category and all of its children are orphaned). Some of these limitations can be addressed through the use of client-side code or stored procedures. With a procedural language we can start at the bottom of the tree and iterate upwards to return the full tree or a single path. We can also use procedural programming to delete nodes without orphaning entire sub-trees by promoting one child element and re-ordering the remaining children to point to the new parent.
The Nested Set Model
What I would like to focus on in this article is a different approach, commonly referred to as the Nested Set Model. In the Nested Set Model, we can look at our hierarchy in a new way, not as nodes and lines, but as nested containers. Try picturing our electronics categories this way:

Notice how our hierarchy is still maintained, as parent categories envelop their children.We represent this form of hierarchy in a table through the use of left and right values to represent the nesting of our nodes:
CREATE TABLE nested_category ( category_id INT AUTO_INCREMENT PRIMARY KEY, name VARCHAR(20) NOT NULL, lft INT NOT NULL, rgt INT NOT NULL ); INSERT INTO nested_category VALUES(1,'ELECTRONICS',1,20),(2,'TELEVISIONS',2,9),(3,'TUBE',3,4), (4,'LCD',5,6),(5,'PLASMA',7,8),(6,'PORTABLE ELECTRONICS',10,19), (7,'MP3 PLAYERS',11,14),(8,'FLASH',12,13), (9,'CD PLAYERS',15,16),(10,'2 WAY RADIOS',17,18); SELECT * FROM nested_category ORDER BY category_id; +-------------+----------------------+-----+-----+ | category_id | name | lft | rgt | +-------------+----------------------+-----+-----+ | 1 | ELECTRONICS | 1 | 20 | | 2 | TELEVISIONS | 2 | 9 | | 3 | TUBE | 3 | 4 | | 4 | LCD | 5 | 6 | | 5 | PLASMA | 7 | 8 | | 6 | PORTABLE ELECTRONICS | 10 | 19 | | 7 | MP3 PLAYERS | 11 | 14 | | 8 | FLASH | 12 | 13 | | 9 | CD PLAYERS | 15 | 16 | | 10 | 2 WAY RADIOS | 17 | 18 | +-------------+----------------------+-----+-----+
We use lft and rgt because left and right are reserved words in MySQL, see http://dev.mysql.com/doc/mysql/en/reserved-words.html for the full list of reserved words.
So how do we determine left and right values? We start numbering at the leftmost side of the outer node and continue to the right:

This design can be applied to a typical tree as well:

When working with a tree, we work from left to right, one layer at a time, descending to each node's children before assigning a right-hand number and moving on to the right. This approach is called the modified preorder tree traversal algorithm.
Retrieving a Full Tree
We can retrieve the full tree through the use of a self-join that links parents with nodes on the basis that a node's lft value will always appear between its parent's lft and rgt values:
SELECT node.name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt AND parent.name = 'ELECTRONICS' ORDER BY node.lft; +----------------------+ | name | +----------------------+ | ELECTRONICS | | TELEVISIONS | | TUBE | | LCD | | PLASMA | | PORTABLE ELECTRONICS | | MP3 PLAYERS | | FLASH | | CD PLAYERS | | 2 WAY RADIOS | +----------------------+
Unlike our previous examples with the adjacency list model, this query will work regardless of the depth of the tree. We do not concern ourselves with the rgt value of the node in our BETWEEN clause because the rgt value will always fall within the same parent as the lft values.
Finding all the Leaf Nodes
Finding all leaf nodes in the nested set model even simpler than the LEFT JOIN method used in the adjacency list model. If you look at the nested_category table, you may notice that the lft and rgt values for leaf nodes are consecutive numbers. To find the leaf nodes, we look for nodes where rgt = lft + 1:
SELECT name FROM nested_category WHERE rgt = lft + 1; +--------------+ | name | +--------------+ | TUBE | | LCD | | PLASMA | | FLASH | | CD PLAYERS | | 2 WAY RADIOS | +--------------+
Retrieving a Single Path
With the nested set model, we can retrieve a single path without having multiple self-joins:
SELECT parent.name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node.name = 'FLASH' ORDER BY node.lft; +----------------------+ | name | +----------------------+ | ELECTRONICS | | PORTABLE ELECTRONICS | | MP3 PLAYERS | | FLASH | +----------------------+
Finding the Depth of the Nodes
We have already looked at how to show the entire tree, but what if we want to also show the depth of each node in the tree, to better identify how each node fits in the hierarchy? This can be done by adding a COUNT function and a GROUP BY clause to our existing query for showing the entire tree:
SELECT node.name, (COUNT(parent.name) - 1) AS depth FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.name ORDER BY node.lft; +----------------------+-------+ | name | depth | +----------------------+-------+ | ELECTRONICS | 0 | | TELEVISIONS | 1 | | TUBE | 2 | | LCD | 2 | | PLASMA | 2 | | PORTABLE ELECTRONICS | 1 | | MP3 PLAYERS | 2 | | FLASH | 3 | | CD PLAYERS | 2 | | 2 WAY RADIOS | 2 | +----------------------+-------+
We can use the depth value to indent our category names with the CONCAT and REPEAT string functions:
SELECT CONCAT( REPEAT(' ', COUNT(parent.name) - 1), node.name) AS name
FROM nested_category AS node,
nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt
GROUP BY node.name
ORDER BY node.lft;
+-----------------------+
| name |
+-----------------------+
| ELECTRONICS |
| TELEVISIONS |
| TUBE |
| LCD |
| PLASMA |
| PORTABLE ELECTRONICS |
| MP3 PLAYERS |
| FLASH |
| CD PLAYERS |
| 2 WAY RADIOS |
+-----------------------+
Of course, in a client-side application you will be more likely to use the depth value directly to display your hierarchy. Web developers could loop through the tree, adding
Depth of a Sub-Tree
When we need depth information for a sub-tree, we cannot limit either the node or parent tables in our self-join because it will corrupt our results. Instead, we add a third self-join, along with a sub-query to determine the depth that will be the new starting point for our sub-tree:
SELECT node.name, (COUNT(parent.name) - (sub_tree.depth + 1)) AS depth FROM nested_category AS node, nested_category AS parent, nested_category AS sub_parent, ( SELECT node.name, (COUNT(parent.name) - 1) AS depth FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node.name = 'PORTABLE ELECTRONICS' GROUP BY node.name ORDER BY node.lft )AS sub_tree WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node.lft BETWEEN sub_parent.lft AND sub_parent.rgt AND sub_parent.name = sub_tree.name GROUP BY node.name ORDER BY node.lft; +----------------------+-------+ | name | depth | +----------------------+-------+ | PORTABLE ELECTRONICS | 0 | | MP3 PLAYERS | 1 | | FLASH | 2 | | CD PLAYERS | 1 | | 2 WAY RADIOS | 1 | +----------------------+-------+
This function can be used with any node name, including the root node. The depth values are always relative to the named node.
Find the Immediate Subordinates of a Node
Imagine you are showing a category of electronics products on a retailer web site. When a user clicks on a category, you would want to show the products of that category, as well as list its immediate sub-categories, but not the entire tree of categories beneath it. For this, we need to show the node and its immediate sub-nodes, but no further down the tree. For example, when showing the PORTABLE ELECTRONICS category, we will want to show MP3 PLAYERS, CD PLAYERS, and 2 WAY RADIOS, but not FLASH.
This can be easily accomplished by adding a HAVING clause to our previous query:
SELECT node.name, (COUNT(parent.name) - (sub_tree.depth + 1)) AS depth
FROM nested_category AS node,
nested_category AS parent,
nested_category AS sub_parent,
(
SELECT node.name, (COUNT(parent.name) - 1) AS depth
FROM nested_category AS node,
nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt
AND node.name = 'PORTABLE ELECTRONICS'
GROUP BY node.name
ORDER BY node.lft
)AS sub_tree
WHERE node.lft BETWEEN parent.lft AND parent.rgt
AND node.lft BETWEEN sub_parent.lft AND sub_parent.rgt
AND sub_parent.name = sub_tree.name
GROUP BY node.name
HAVING depth
<p>If you do not wish to show the parent node, change the <strong>HAVING depth .</strong></p>
<h3 id="Aggregate-Functions-in-a-Nested-Set">Aggregate Functions in a Nested Set</h3>
<p>Let's add a table of products that we can use to demonstrate aggregate functions with:</p><pre class="brush:php;toolbar:false">CREATE TABLE product(
product_id INT AUTO_INCREMENT PRIMARY KEY,
name VARCHAR(40),
category_id INT NOT NULL
);
INSERT INTO product(name, category_id) VALUES('20" TV',3),('36" TV',3),
('Super-LCD 42"',4),('Ultra-Plasma 62"',5),('Value Plasma 38"',5),
('Power-MP3 5gb',7),('Super-Player 1gb',8),('Porta CD',9),('CD To go!',9),
('Family Talk 360',10);
SELECT * FROM product;
+------------+-------------------+-------------+
| product_id | name | category_id |
+------------+-------------------+-------------+
| 1 | 20" TV | 3 |
| 2 | 36" TV | 3 |
| 3 | Super-LCD 42" | 4 |
| 4 | Ultra-Plasma 62" | 5 |
| 5 | Value Plasma 38" | 5 |
| 6 | Power-MP3 128mb | 7 |
| 7 | Super-Shuffle 1gb | 8 |
| 8 | Porta CD | 9 |
| 9 | CD To go! | 9 |
| 10 | Family Talk 360 | 10 |
+------------+-------------------+-------------+
Now let's produce a query that can retrieve our category tree, along with a product count for each category:
SELECT parent.name, COUNT(product.name) FROM nested_category AS node , nested_category AS parent, product WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node.category_id = product.category_id GROUP BY parent.name ORDER BY node.lft; +----------------------+---------------------+ | name | COUNT(product.name) | +----------------------+---------------------+ | ELECTRONICS | 10 | | TELEVISIONS | 5 | | TUBE | 2 | | LCD | 1 | | PLASMA | 2 | | PORTABLE ELECTRONICS | 5 | | MP3 PLAYERS | 2 | | FLASH | 1 | | CD PLAYERS | 2 | | 2 WAY RADIOS | 1 | +----------------------+---------------------+
This is our typical whole tree query with a COUNT and GROUP BY added, along with a reference to the product table and a join between the node and product table in the WHERE clause. As you can see, there is a count for each category and the count of subcategories is reflected in the parent categories.
Adding New Nodes
Now that we have learned how to query our tree, we should take a look at how to update our tree by adding a new node. Let's look at our nested set diagram again:

If we wanted to add a new node between the TELEVISIONS and PORTABLE ELECTRONICS nodes, the new node would have lft and rgt values of 10 and 11, and all nodes to its right would have their lft and rgt values increased by two. We would then add the new node with the appropriate lft and rgt values. While this can be done with a stored procedure in MySQL 5, I will assume for the moment that most readers are using 4.1, as it is the latest stable version, and I will isolate my queries with a LOCK TABLES statement instead:
LOCK TABLE nested_category WRITE;
SELECT @myRight := rgt FROM nested_category
WHERE name = 'TELEVISIONS';
UPDATE nested_category SET rgt = rgt + 2 WHERE rgt > @myRight;
UPDATE nested_category SET lft = lft + 2 WHERE lft > @myRight;
INSERT INTO nested_category(name, lft, rgt) VALUES('GAME CONSOLES', @myRight + 1, @myRight + 2);
UNLOCK TABLES;
We can then check our nesting with our indented tree query:
SELECT CONCAT( REPEAT( ' ', (COUNT(parent.name) - 1) ), node.name) AS name
FROM nested_category AS node,
nested_category AS parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt
GROUP BY node.name
ORDER BY node.lft;
+-----------------------+
| name |
+-----------------------+
| ELECTRONICS |
| TELEVISIONS |
| TUBE |
| LCD |
| PLASMA |
| GAME CONSOLES |
| PORTABLE ELECTRONICS |
| MP3 PLAYERS |
| FLASH |
| CD PLAYERS |
| 2 WAY RADIOS |
+-----------------------+
If we instead want to add a node as a child of a node that has no existing children, we need to modify our procedure slightly. Let's add a new FRS node below the 2 WAY RADIOS node:
LOCK TABLE nested_category WRITE;
SELECT @myLeft := lft FROM nested_category
WHERE name = '2 WAY RADIOS';
UPDATE nested_category SET rgt = rgt + 2 WHERE rgt > @myLeft;
UPDATE nested_category SET lft = lft + 2 WHERE lft > @myLeft;
INSERT INTO nested_category(name, lft, rgt) VALUES('FRS', @myLeft + 1, @myLeft + 2);
UNLOCK TABLES;
In this example we expand everything to the right of the left-hand number of our proud new parent node, then place the node to the right of the left-hand value. As you can see, our new node is now properly nested:
SELECT CONCAT( REPEAT( ' ', (COUNT(parent.name) - 1) ), node.name) AS name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.name ORDER BY node.lft; +-----------------------+ | name | +-----------------------+ | ELECTRONICS | | TELEVISIONS | | TUBE | | LCD | | PLASMA | | GAME CONSOLES | | PORTABLE ELECTRONICS | | MP3 PLAYERS | | FLASH | | CD PLAYERS | | 2 WAY RADIOS | | FRS | +-----------------------+
Deleting Nodes
The last basic task involved in working with nested sets is the removal of nodes. The course of action you take when deleting a node depends on the node's position in the hierarchy; deleting leaf nodes is easier than deleting nodes with children because we have to handle the orphaned nodes.
When deleting a leaf node, the process if just the opposite of adding a new node, we delete the node and its width from every node to its right:
LOCK TABLE nested_category WRITE; SELECT @myLeft := lft, @myRight := rgt, @myWidth := rgt - lft + 1 FROM nested_category WHERE name = 'GAME CONSOLES'; DELETE FROM nested_category WHERE lft BETWEEN @myLeft AND @myRight; UPDATE nested_category SET rgt = rgt - @myWidth WHERE rgt > @myRight; UPDATE nested_category SET lft = lft - @myWidth WHERE lft > @myRight; UNLOCK TABLES;
And once again, we execute our indented tree query to confirm that our node has been deleted without corrupting the hierarchy:
SELECT CONCAT( REPEAT( ' ', (COUNT(parent.name) - 1) ), node.name) AS name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.name ORDER BY node.lft; +-----------------------+ | name | +-----------------------+ | ELECTRONICS | | TELEVISIONS | | TUBE | | LCD | | PLASMA | | PORTABLE ELECTRONICS | | MP3 PLAYERS | | FLASH | | CD PLAYERS | | 2 WAY RADIOS | | FRS | +-----------------------+
This approach works equally well to delete a node and all its children:
LOCK TABLE nested_category WRITE; SELECT @myLeft := lft, @myRight := rgt, @myWidth := rgt - lft + 1 FROM nested_category WHERE name = 'MP3 PLAYERS'; DELETE FROM nested_category WHERE lft BETWEEN @myLeft AND @myRight; UPDATE nested_category SET rgt = rgt - @myWidth WHERE rgt > @myRight; UPDATE nested_category SET lft = lft - @myWidth WHERE lft > @myRight; UNLOCK TABLES;
And once again, we query to see that we have successfully deleted an entire sub-tree:
SELECT CONCAT( REPEAT( ' ', (COUNT(parent.name) - 1) ), node.name) AS name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.name ORDER BY node.lft; +-----------------------+ | name | +-----------------------+ | ELECTRONICS | | TELEVISIONS | | TUBE | | LCD | | PLASMA | | PORTABLE ELECTRONICS | | CD PLAYERS | | 2 WAY RADIOS | | FRS | +-----------------------+
The other scenario we have to deal with is the deletion of a parent node but not the children. In some cases you may wish to just change the name to a placeholder until a replacement is presented, such as when a supervisor is fired. In other cases, the child nodes should all be moved up to the level of the deleted parent:
LOCK TABLE nested_category WRITE; SELECT @myLeft := lft, @myRight := rgt, @myWidth := rgt - lft + 1 FROM nested_category WHERE name = 'PORTABLE ELECTRONICS'; DELETE FROM nested_category WHERE lft = @myLeft; UPDATE nested_category SET rgt = rgt - 1, lft = lft - 1 WHERE lft BETWEEN @myLeft AND @myRight; UPDATE nested_category SET rgt = rgt - 2 WHERE rgt > @myRight; UPDATE nested_category SET lft = lft - 2 WHERE lft > @myRight; UNLOCK TABLES;
In this case we subtract two from all elements to the right of the node (since without children it would have a width of two), and one from the nodes that are its children (to close the gap created by the loss of the parent's left value). Once again, we can confirm our elements have been promoted:
SELECT CONCAT( REPEAT( ' ', (COUNT(parent.name) - 1) ), node.name) AS name FROM nested_category AS node, nested_category AS parent WHERE node.lft BETWEEN parent.lft AND parent.rgt GROUP BY node.name ORDER BY node.lft; +---------------+ | name | +---------------+ | ELECTRONICS | | TELEVISIONS | | TUBE | | LCD | | PLASMA | | CD PLAYERS | | 2 WAY RADIOS | | FRS | +---------------+
Other scenarios when deleting nodes would include promoting one of the children to the parent position and moving the child nodes under a sibling of the parent node, but for the sake of space these scenarios will not be covered in this article.

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)
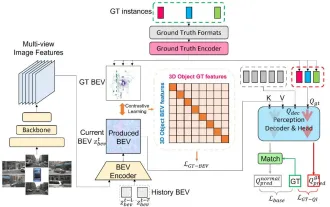 CLIP-BEVFormer:显式监督BEVFormer结构,提升长尾检测性能
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer:显式监督BEVFormer结构,提升长尾检测性能
Mar 26, 2024 pm 12:41 PM
写在前面&笔者的个人理解目前,在整个自动驾驶系统当中,感知模块扮演了其中至关重要的角色,行驶在道路上的自动驾驶车辆只有通过感知模块获得到准确的感知结果后,才能让自动驾驶系统中的下游规控模块做出及时、正确的判断和行为决策。目前,具备自动驾驶功能的汽车中通常会配备包括环视相机传感器、激光雷达传感器以及毫米波雷达传感器在内的多种数据信息传感器来收集不同模态的信息,用于实现准确的感知任务。基于纯视觉的BEV感知算法因其较低的硬件成本和易于部署的特点,以及其输出结果能便捷地应用于各种下游任务,因此受到工业
 今日头条发布文章怎么才能有收益?今日头条发布文章获得更多收益方法!
Mar 15, 2024 pm 04:13 PM
今日头条发布文章怎么才能有收益?今日头条发布文章获得更多收益方法!
Mar 15, 2024 pm 04:13 PM
一、今日头条发布文章怎么才能有收益?今日头条发布文章获得更多收益方法!1.开通基础权益:原创文章选择投放广告可获得收益,视频必须要原创横屏才会有收益。2.开通百粉权益:粉丝量达到百粉以上,微头条、原创问答创作及问答均可获得收益。3.坚持原创作品:原创作品包含文章、微头条及问题等,要求300字以上。注意违规抄袭作品作为原创发布,会被扣信用分,即使有收益也会被扣除。4.垂直度:做专业领域一类的文章,不能随意跨领域写文章,会得不到合适的推荐,达不到作品的专和精,难以吸引粉丝读者。5.活跃度:活跃度高,
 使用C++实现机器学习算法:常见挑战及解决方案
Jun 03, 2024 pm 01:25 PM
使用C++实现机器学习算法:常见挑战及解决方案
Jun 03, 2024 pm 01:25 PM
C++中机器学习算法面临的常见挑战包括内存管理、多线程、性能优化和可维护性。解决方案包括使用智能指针、现代线程库、SIMD指令和第三方库,并遵循代码风格指南和使用自动化工具。实践案例展示了如何利用Eigen库实现线性回归算法,有效地管理内存和使用高性能矩阵操作。
 探究C++sort函数的底层原理与算法选择
Apr 02, 2024 pm 05:36 PM
探究C++sort函数的底层原理与算法选择
Apr 02, 2024 pm 05:36 PM
C++sort函数底层采用归并排序,其复杂度为O(nlogn),并提供不同的排序算法选择,包括快速排序、堆排序和稳定排序。
 人工智能可以预测犯罪吗?探索CrimeGPT的能力
Mar 22, 2024 pm 10:10 PM
人工智能可以预测犯罪吗?探索CrimeGPT的能力
Mar 22, 2024 pm 10:10 PM
人工智能(AI)与执法领域的融合为犯罪预防和侦查开辟了新的可能性。人工智能的预测能力被广泛应用于CrimeGPT(犯罪预测技术)等系统,用于预测犯罪活动。本文探讨了人工智能在犯罪预测领域的潜力、目前的应用情况、所面临的挑战以及相关技术可能带来的道德影响。人工智能和犯罪预测:基础知识CrimeGPT利用机器学习算法来分析大量数据集,识别可以预测犯罪可能发生的地点和时间的模式。这些数据集包括历史犯罪统计数据、人口统计信息、经济指标、天气模式等。通过识别人类分析师可能忽视的趋势,人工智能可以为执法机构
 改进的检测算法:用于高分辨率光学遥感图像目标检测
Jun 06, 2024 pm 12:33 PM
改进的检测算法:用于高分辨率光学遥感图像目标检测
Jun 06, 2024 pm 12:33 PM
01前景概要目前,难以在检测效率和检测结果之间取得适当的平衡。我们就研究出了一种用于高分辨率光学遥感图像中目标检测的增强YOLOv5算法,利用多层特征金字塔、多检测头策略和混合注意力模块来提高光学遥感图像的目标检测网络的效果。根据SIMD数据集,新算法的mAP比YOLOv5好2.2%,比YOLOX好8.48%,在检测结果和速度之间实现了更好的平衡。02背景&动机随着远感技术的快速发展,高分辨率光学远感图像已被用于描述地球表面的许多物体,包括飞机、汽车、建筑物等。目标检测在远感图像的解释中
 算法在 58 画像平台建设中的应用
May 09, 2024 am 09:01 AM
算法在 58 画像平台建设中的应用
May 09, 2024 am 09:01 AM
一、58画像平台建设背景首先和大家分享下58画像平台的建设背景。1.传统的画像平台传统的思路已经不够,建设用户画像平台依赖数据仓库建模能力,整合多业务线数据,构建准确的用户画像;还需要数据挖掘,理解用户行为、兴趣和需求,提供算法侧的能力;最后,还需要具备数据平台能力,高效存储、查询和共享用户画像数据,提供画像服务。业务自建画像平台和中台类型画像平台主要区别在于,业务自建画像平台服务单条业务线,按需定制;中台平台服务多条业务线,建模复杂,提供更为通用的能力。2.58中台画像建设的背景58的用户画像
 实时加SOTA一飞冲天!FastOcc:推理更快、部署友好Occ算法来啦!
Mar 14, 2024 pm 11:50 PM
实时加SOTA一飞冲天!FastOcc:推理更快、部署友好Occ算法来啦!
Mar 14, 2024 pm 11:50 PM
写在前面&笔者的个人理解在自动驾驶系统当中,感知任务是整个自驾系统中至关重要的组成部分。感知任务的主要目标是使自动驾驶车辆能够理解和感知周围的环境元素,如行驶在路上的车辆、路旁的行人、行驶过程中遇到的障碍物、路上的交通标志等,从而帮助下游模块做出正确合理的决策和行为。在一辆具备自动驾驶功能的车辆中,通常会配备不同类型的信息采集传感器,如环视相机传感器、激光雷达传感器以及毫米波雷达传感器等等,从而确保自动驾驶车辆能够准确感知和理解周围环境要素,使自动驾驶车辆在自主行驶的过程中能够做出正确的决断。目






