对于排序算法,这些年用到的也不多,基本处于拿来用的状态,一直没有花时间稍微深入了解。最近下定决心自己动手写写,加深理解。查看了不少资料,有不少分析的很到位,帮助快速理解,在此感谢!
1、概念理解及实现
package com.demo.algorithm.sort;
/**
* 排序算法合集
* @author sheungxin
*
*/
public class NumberSort {
/**
* 插入排序-直接插入排序
* 工作原理:构建有序序列,对于未排序的数据,在已排序序列中从后向前扫描,找到相应位置并插入
* 参考:http://blog.csdn.net/morewindows/article/details/6665714
* @param array
* @param asc 0:升序 1:降序
*/
public static void straightInsertSort(int[] array,int asc){
int tmp,n;
//从第二位元素开始,第一位认为已被排序
for(int m=1;m<array.length;m++){
tmp=array[m];
//在已排序序列中从后向前扫描,若该元素>(<)新元素,将该新元素向后移一位
for(n=m-1;n>=0&&(asc==1&&tmp>array[n]||asc==0&&tmp<array[n]);n--){
array[n+1]=array[n];
}
//上述循环在该元素<=(>=)新元素或者扫描到首位时结束,将该元素插入在结束位置后面
array[n+1]=tmp;
}
display(array);
}
/**
* 插入排序-希尔排序,实质就是分组排序,又称缩小增量排序
* 工作原理:先将整个待排序元素序列分割成若干个子序列(由相隔某个“增量”元素组成)分别进行直接插入排序,
* 然后依次缩减增量再进行排序,待整个序列中元素基本有序(增量足够小)时,再进行一次全元素直接插入排序。
* 优势:直接插入排序在元素基本有序的情况下,效率最高
* 参考:http://blog.csdn.net/morewindows/article/details/6668714
* @param array
* @param asc 0:升序 1:降序
*/
public static void shellSort(int[] array,int asc){
int len=array.length;
//依次缩减增量,直到增量为1
for(int gap=len/2;gap>0;gap/=2){
//根据步长把待排序元素分为gap组
for(int i=0;i<gap;i++){
//分别对每组元素进行直接插入排序,从i开始以增加gap得到一组元素
for(int j=i+gap;j<len;j+=gap){
int tmp=array[j];
int k=j-gap;//上一个节点
//在已排序序列中从后向前扫描,若该元素>(<)新元素,将该新元素向后移一位
while(k>=0&&(asc==1&&tmp>array[k]||asc==0&&tmp<array[k])){
array[k+gap]=array[k];
k-=gap;//向前扫描,移到下标
}
//上述循环在该元素<=(>=)新元素或者扫描到首位时结束,将该元素插入在结束位置后面
array[k+gap]=tmp;
}
}
}
display(array);
}
/**
* 选择排序:简单选择排序
* 原理:从无序区中选择一个最小的元素之间放到有序区的最后
* 参考:http://blog.csdn.net/morewindows/article/details/6671824
* @param array
* @param asc 0:升序 1:降序
*/
public static void selectSort(int[] array,int asc){
int tmp,ix;
for(int i=0;i<array.length;i++){
ix=i;//最小或最大元素的位置
//从无序区中选择一个最小或最大的元素的位置
for(int j=i+1;j<array.length;j++){
if((asc==0&&array[ix]>array[j])||(asc==1&&array[ix]<array[j])){
ix=j;
}
}
//交换位置
if(ix!=i){
tmp=array[i];
array[i]=array[ix];
array[ix]=tmp;
}
}
display(array);
}
/**
* 选择排序:堆排序
* 原理:二叉堆近似二叉树,父节点总是大于或等于(小于或等于)任何一个子节点
* 参考:http://blog.csdn.net/morewindows/article/details/6709644
* http://blog.csdn.net/kimylrong/article/details/17150475
* @param array
* @param asc 0:升序 1:降序
*/
public static void heapSort(int[] array,int asc){
//构建二叉堆,从最后一个父节点开始
for(int i=array.length/2-1;i>=0;i--){
buildHeap(array, array.length, i, asc);
}
//使用堆根节点构建有序序列
for(int i=array.length-1;i>=1;i--){
//依次把根节点向后交换构建有序序列
swapArray(array, 0, i);
//根节点交换位置后,从0,i-1重新构建堆
buildHeap(array, i, 0, asc);
}
display(array);
}
/**
* 构建二叉堆
* @param array 二叉堆数组
* @param heapSize 二叉堆大小
* @param index 当前父节点位置
* @param asc 0:升序 1:降序
*/
private static void buildHeap(int[] array,int heapSize,int index,int asc){
//比较父节点、左右叶子节点,找出最大或最小节点位置
int left = index * 2 + 1;
int right = index * 2 + 2;
int ix=index;
if(left<heapSize&&(asc==1&&array[index]>array[left]||asc==0&&array[index]<array[left])){
ix=left;
}
if(right<heapSize&&(asc==1&&array[ix]>array[right]||asc==0&&array[ix]<array[right])){
ix=right;
}
if(ix!=index){
swapArray(array, index, ix);//交换父节点和叶子节点位置,满足最大/小堆性质
//递归向下交换,非最下层父节点与叶子节点交换会破坏下层最大/小堆性质
buildHeap(array, heapSize, ix, asc);
}
}
/**
* 交换排序:冒泡排序
* 参考: http://blog.csdn.net/morewindows/article/details/6657829
* @param array
* @param asc 0:升序 1:降序
*/
public static void bubbleSort(int[] array,int asc){
for(int i=0;i<array.length;i++){
for(int j=1;j<array.length-i;j++){
if((asc==0&&array[j-1]>array[j])||(asc==1&&array[j-1]<array[j])){
swapArray(array, j-1, j);
}
}
}
/**有点像交换排序、直接插入排序,交换次数过多
//从第二个元素开始依次与其左边元素进行比较
for(int m=1;m<array.length;m++){
//从左边最远的元素开始比较
for(int n=0;n<m;n++){
//满足条件交换位置
if((asc==0&&array[m]>array[n])
||(asc==1&&array[m]<array[n])){
swapArray(array, m, n);
}
}
}**/
display(array);
}
/**
* 交换排序:快速排序,在同为O(N*logN)的几种排序算法中效率较高,经常被使用
* 原理:从元素序列中取一个数作为基准数,左右分别放大于或小于的元素,再对左右区间重复上述操作,直到各区间只有一个数
* 参考: http://blog.csdn.net/morewindows/article/details/6684558
* @param array
* @param asc 0:升序 1:降序
*/
public static void quickSort(int[] array,int l,int r,int asc){
if(l<r){
int tmp=array[l];//把第一个节点作为基准数,视为第一个空位
int i=l;
int j=r;
//以基准数为标准,左右分别放大于或小于的节点
while(i<j){
//寻找右边小于(大于)基准数的节点位置
while(i<j&&(asc==0&&array[j]>=tmp||asc==1&&array[j]<=tmp)){
j--;
}
//把右边找到的节点放到左边的空位
array[i]=array[j];
//寻找右边大于(小于)基准数的节点位置
while(i<j&&(asc==0&&array[i]<=tmp||asc==1&&array[i]>=tmp)){
i++;
}
//把左边找到的节点放到右边的空位
array[j]=array[i];
}
//把基准数放在中间节点
array[i]=tmp;
//对中间点左边的元素重复上述操作
quickSort(array, l, i-1, asc);
//对中间点右边的元素重复上述操作
quickSort(array, i+1, r, asc);
}
display(array);
}
/**
* 归并排序:将两个(或两个以上)有序表合并成一个新的有序表
* 原理:将序列不断拆分,再反向两两合并形成有序序列
* 时间复杂度:O(nlogn)
* 参考:http://www.cnblogs.com/jingmoxukong/p/4308823.html
* @param array
* @param l 左指针
* @param r 右指针
* @param asc 0:升序 1:降序
*/
public static void mergeSort(int[] array,int l,int r,int asc){
//找出中间点,左右拆分为两个序列
int m=(l+r)/2;
if(l<r){
//左边序列,递归拆分直到间隔为0
mergeSort(array, l, m, asc);
//右边,递归拆分直到间隔为0
mergeSort(array, m+1, r, asc);
//左右归并
merge(array, l, m, r, asc);
}
display(array);
}
/**
* 左右归并为有序集合
* @param array
* @param l 左指针
* @param m 中间指针
* @param r 右指针
*/
private static void merge(int[] array,int l,int m,int r,int asc){
int[] tmp=new int[r-l+1];
int i=l;//左指针
int j=m+1;//右指针
int k=0;
//把较小的数先移到临时数组中
while(i<=m&&j<=r){
if(asc==0&&array[i]<array[j]||asc==1&&array[i]>array[j]){
tmp[k++]=array[i++];
}else{
tmp[k++]=array[j++];
}
}
//把左边剩余的数移到数组中
while(i<=m){
tmp[k++]=array[i++];
}
//把右边剩余的数移到数组中
while(j<=r){
tmp[k++]=array[j++];
}
//把临时数组中的数覆盖原数组,形成有序集合
for(k=0;k<tmp.length;k++){
array[l+k]=tmp[k];
}
}
/**
* 基数/桶排序:将序列分到有限数量的桶子里,再分别排序
* 原理:将序列分到有限数量的桶子里,再分别排序
* 时间复杂度:O(nlog(r)m),r为所采用的基数,m为堆数
* 参考:http://www.cnblogs.com/jingmoxukong/p/4308823.html
* @param array
* @param l 左指针
* @param r 右指针
* @param asc 0:升序 1:降序
*/
public static void radixSort(int[] array,int digit,int asc){
final int radix=10;//基数,阿拉伯数字0~9,视为10个桶
int i=0;
int j=0;
int[] count=new int[radix];//存放各个桶存放数据的个数
int[] tmp=new int[array.length];
//按照从低到高位进行排序
for(int d=1;d<=digit;d++){
//置空各个桶的统计数据
for(i=0;i<radix;i++){
count[i]=0;
}
//根据位数d,统计各个桶存放数据的个数
for(i=0;i<array.length;i++){
j=array[i]/((Double)Math.pow(10, d-1)).intValue()%10;//d位上的数据
count[j]++;
}
//把count[i]的值由存放的个数改变了有边界的索引
for(i=1;i<radix;i++){
count[i]+=count[i-1];
}
//将数据依次装入临时桶里,从右向左扫描
for(i=array.length-1;i>=0;i--){
j=array[i]/((Double)Math.pow(10, d-1)).intValue()%10;//d位上的数据
tmp[count[j]-1]=array[i];//count[j]-1为第J个桶右边界的下标
count[j]--;//桶j装入数据索引减1
}
//按照桶中数据顺序放入原数据序列中
for(i=0;i<array.length;i++){
if(d==digit){
if(asc==0){
array[i]=tmp[i];
}else{
array[i]=tmp[array.length-i-1];
}
}else{
array[i]=tmp[i];
}
}
}
display(array);
}
/**
* 数组中指定位置的值交换位置
* @param array
* @param i
* @param j
*/
private static void swapArray(int[] array,int i,int j){
array[i]=array[j]^array[i];
array[j]=array[i]^array[j];
array[i]=array[i]^array[j];
}
/**
* 输出数组
* @param array
*/
private static void display(int[] array){
StringBuilder builder=new StringBuilder("[");
for(int i=0;i<array.length;i++){
builder.append(array[i]);
if(i<array.length-1){
builder.append(",");
}else{
builder.append("]");
}
}
System.out.println(builder.toString());
}
public static void main(String[] args) {
int[] array=new int[]{11,56,35,62,97,21,36,33,86,81,35};
//straightInsertSort(array, 0);
//shellSort(array, 0);
//selectSort(array, 0);
//heapSort(array, 0);
//bubbleSort(array,0);
//quickSort(array, 0, array.length-1, 0);
//mergeSort(array, 0, array.length-1,1);
radixSort(array, 3, 0);
}
}2、排序算法对比图
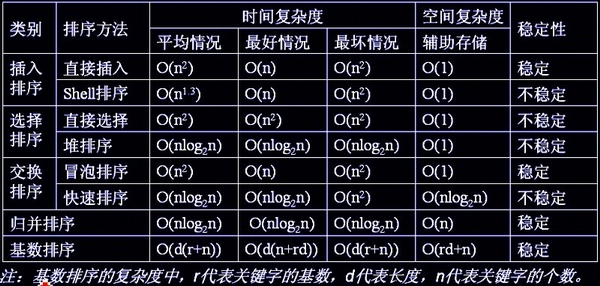
引用
http://blog.csdn.net/hguisu/article/details/7776068
3、选择排序算法准则
影响排序的因素有很多,平均时间复杂度低的算法并不一定就是最优的。相反,有时平均时间复杂度高的算法可能更适合某些特殊情况。同时,选择算法时还得考虑它的可读性,以利于软件的维护。一般而言,需要考虑的因素有以下四点:
1)、待排序的记录数目n的大小;
2)、记录本身数据量的大小,也就是记录中除关键字外的其他信息量的大小;
3)、关键字的结构及其分布情况;
4)、对排序稳定性的要求。
设待排序元素的个数为n.
1)、当n较大,则应采用时间复杂度为O(nlog2n)的排序方法:快速排序、堆排序或归并排序序。
a、快速排序:是目前基于比较的内部排序中被认为是最好的方法,当待排序的关键字是随机分布时,快速排序的平均时间最短;
b、堆排序 :如果内存空间允许且要求稳定性的;
c、归并排序:它有一定数量的数据移动,所以我们可能过与插入排序组合,先获得一定长度的序列,然后再合并,在效率上将有所提高。
2)、当n较大,内存空间允许,且要求稳定性 =》归并排序
3)、当n较小,可采用直接插入或直接选择排序。
a、直接插入排序:当元素分布有序,直接插入排序将大大减少比较次数和移动记录的次数;
b、直接选择排序 :元素分布有序,如果不要求稳定性,选择直接选择排序
4)、一般不使用或不直接使用传统的冒泡排序。
5)、基数排序:它是一种稳定的排序算法,但有一定的局限性:
a、关键字可分解;
b、记录的关键字位数较少,如果密集更好;
c、如果是数字时,最好是无符号的,否则将增加相应的映射复杂度,可先将其正负分开排序。
引用
http://blog.csdn.net/hguisu/article/details/7776068




