详解Python中使用最小二乘法方法
之所以说”使用”而不是”实现”,是因为python的相关类库已经帮我们实现了具体算法,而我们只要学会使用就可以了。随着对技术的逐渐掌握及积累,当类库中的算法已经无法满足自身需求的时候,我们也可以尝试通过自己的方式实现各种算法。
言归正传,什么是”最小二乘法”呢?
定义:最小二乘法(又称最小平方法)是一种数学优化技术,它通过最小化误差的平方和寻找数据的最佳函数匹配。
作用:利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
原则:以”残差平方和最小”确定直线位置(在数理统计中,残差是指实际观察值与估计值之间的差)
基本思路:对于一元线性回归模型, 假设从总体中获取了n组观察值(X1,Y1),(X2,Y2), …,(Xn,Yn),对于平面中的这n个点,可以使用无数条曲线来拟合。而线性回归就是要求样本回归函数尽可能好地拟合这组值,也就是说,这条直线应该尽可能的处于样本数据的中心位置。因此,选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。
实现代码如下,代码中已经详细的给了注释:
##最小二乘法
import numpy as np ##科学计算库
import scipy as sp ##在numpy基础上实现的部分算法库
import matplotlib.pyplot as plt ##绘图库
from scipy.optimize import leastsq ##引入最小二乘法算法
'''
设置样本数据,真实数据需要在这里处理
'''
##样本数据(Xi,Yi),需要转换成数组(列表)形式
Xi=np.array([6.19,2.51,7.29,7.01,5.7,2.66,3.98,2.5,9.1,4.2])
Yi=np.array([5.25,2.83,6.41,6.71,5.1,4.23,5.05,1.98,10.5,6.3])
'''
设定拟合函数和偏差函数
函数的形状确定过程:
1.先画样本图像
2.根据样本图像大致形状确定函数形式(直线、抛物线、正弦余弦等)
'''
##需要拟合的函数func :指定函数的形状
def func(p,x):
k,b=p
return k*x+b
##偏差函数:x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的
def error(p,x,y):
return func(p,x)-y
'''
主要部分:附带部分说明
1.leastsq函数的返回值tuple,第一个元素是求解结果,第二个是求解的代价值(个人理解)
2.官网的原话(第二个值):Value of the cost function at the solution
3.实例:Para=>(array([ 0.61349535, 1.79409255]), 3)
4.返回值元组中第一个值的数量跟需要求解的参数的数量一致
'''
#k,b的初始值,可以任意设定,经过几次试验,发现p0的值会影响cost的值:Para[1]
p0=[1,20]
#把error函数中除了p0以外的参数打包到args中(使用要求)
Para=leastsq(error,p0,args=(Xi,Yi))
#读取结果
k,b=Para[0]
print("k=",k,"b=",b)
print("cost:"+str(Para[1]))
print("求解的拟合直线为:")
print("y="+str(round(k,2))+"x+"+str(round(b,2)))
'''
绘图,看拟合效果.
matplotlib默认不支持中文,label设置中文的话需要另行设置
如果报错,改成英文就可以
'''
#画样本点
plt.figure(figsize=(8,6)) ##指定图像比例: 8:6
plt.scatter(Xi,Yi,color="green",label="样本数据",linewidth=2)
#画拟合直线
x=np.linspace(0,12,100) ##在0-15直接画100个连续点
y=k*x+b ##函数式
plt.plot(x,y,color="red",label="拟合直线",linewidth=2)
plt.legend() #绘制图例
plt.show()结果如下所示:
输出结果:
k= 0.900458420439 b= 0.831055638877
cost:1
求解的拟合直线为:
y=0.9x+0.83
绘图结果:
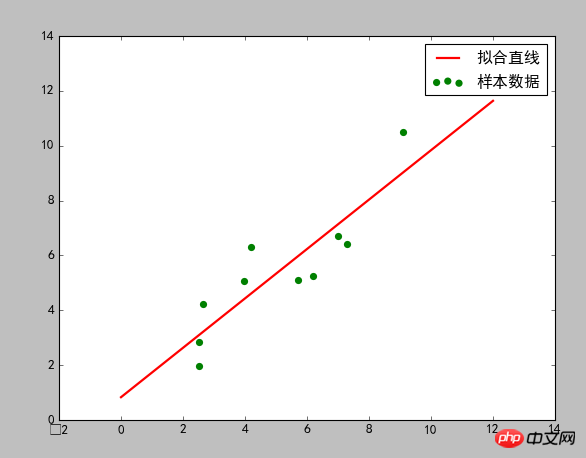
以上是详解Python中使用最小二乘法方法的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

AI Hentai Generator
免费生成ai无尽的。

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)

热门话题
 C语言 sum 的作用是什么?
Apr 03, 2025 pm 02:21 PM
C语言 sum 的作用是什么?
Apr 03, 2025 pm 02:21 PM
C语言中没有内置求和函数,需自行编写。可通过遍历数组并累加元素实现求和:循环版本:使用for循环和数组长度计算求和。指针版本:使用指针指向数组元素,通过自增指针遍历高效求和。动态分配数组版本:动态分配数组并自行管理内存,确保释放已分配内存以防止内存泄漏。
 谁得到更多的Python或JavaScript?
Apr 04, 2025 am 12:09 AM
谁得到更多的Python或JavaScript?
Apr 04, 2025 am 12:09 AM
Python和JavaScript开发者的薪资没有绝对的高低,具体取决于技能和行业需求。1.Python在数据科学和机器学习领域可能薪资更高。2.JavaScript在前端和全栈开发中需求大,薪资也可观。3.影响因素包括经验、地理位置、公司规模和特定技能。
 H5页面制作是否需要持续维护
Apr 05, 2025 pm 11:27 PM
H5页面制作是否需要持续维护
Apr 05, 2025 pm 11:27 PM
H5页面需要持续维护,这是因为代码漏洞、浏览器兼容性、性能优化、安全更新和用户体验提升等因素。有效维护的方法包括建立完善的测试体系、使用版本控制工具、定期监控页面性能、收集用户反馈和制定维护计划。
 distinctIdistinguish有关系吗
Apr 03, 2025 pm 10:30 PM
distinctIdistinguish有关系吗
Apr 03, 2025 pm 10:30 PM
distinct 和 distinguish 虽都与区分有关,但用法不同:distinct(形容词)描述事物本身的独特性,用于强调事物之间的差异;distinguish(动词)表示区分行为或能力,用于描述辨别过程。在编程中,distinct 常用于表示集合中元素的唯一性,如去重操作;distinguish 则体现在算法或函数的设计中,如区分奇数和偶数。优化时,distinct 操作应选择合适的算法和数据结构,而 distinguish 操作应优化区分逻辑效率,并注意编写清晰可读的代码。
 如何理解 C 语言中的 !x?
Apr 03, 2025 pm 02:33 PM
如何理解 C 语言中的 !x?
Apr 03, 2025 pm 02:33 PM
!x 的理解!x 是 C 语言中的逻辑非运算符,对 x 的值进行布尔取反,即真变假,假变真。但要注意,C 语言中真假由数值而非布尔类型表示,非零视为真,只有 0 才视为假。因此,!x 对负数的处理与正数相同,都视为真。
 C语言中 sum 是什么意思?
Apr 03, 2025 pm 02:36 PM
C语言中 sum 是什么意思?
Apr 03, 2025 pm 02:36 PM
C语言中没有内置的sum函数用于求和,但可以通过以下方法实现:使用循环逐个累加元素;使用指针逐个访问并累加元素;对于大数据量,考虑并行计算。
 如何获取58同城工作页面上的实时申请和浏览人数数据?
Apr 05, 2025 am 08:06 AM
如何获取58同城工作页面上的实时申请和浏览人数数据?
Apr 05, 2025 am 08:06 AM
如何在爬虫时获取58同城工作页面的动态数据?在使用爬虫工具爬取58同城的某个工作页面时,可能会遇到这样�...
 爱心代码复制粘贴 爱心代码免费复制粘贴手机
Apr 04, 2025 am 06:48 AM
爱心代码复制粘贴 爱心代码免费复制粘贴手机
Apr 04, 2025 am 06:48 AM
复制粘贴代码并非不可行,但需谨慎对待。代码中环境、库、版本等依赖项可能与当前项目不匹配,导致错误或不可预料的结果。务必确保上下文一致,包括文件路径、依赖库和 Python 版本。此外,复制粘贴特定库的代码时,可能需要安装该库及其依赖项。常见的错误包括路径错误、版本冲突和代码风格不一致。性能优化需根据代码原用途和约束重新设计或重构。理解并调试复制的代码至关重要,切勿盲目复制粘贴。






