无限极分类的三种方式（迭代、递归、引用）
一般的分类树状结构有两种方式：
一种是adjacency list，也就是是id，parent id这中形式。
另一种是nested set，即左右值的形式。
左右值形式查询起来比较高效，无需递归等，推荐使用，但是没有pid形式简单直观，而且有些旧的数据库类似地区等结构设计一直是pid这种形式（貌似也有算法可以将两者转换，不做深入了解），所以。。。
下面所说的都为adjacency list的形式，数据表格式类似id,pid,name这种格式。
通常来说是将数据全部从数据库读取后，然后再组装数组来实现，当然也可以每次递归等都查询数据库，但是会造成数据库压力，且不容易封装成方法，不建议这样做。
目前来说常用的有三种方式，我们来实现select下拉菜单展示的样式：
1、首先是最常用最普通，同样也是效率最低的递归方法：就是不停的foreach循环递归。
function getTreeOptions3($list, $pid = 0)
{ $options = []; foreach ($list as $key => $value) { if ($value['id'] == $pid) {//查看是否为子元素，如果是则递归继续查询
$options[$value['id']] = $value['name']; unset($list[$key]);//销毁已查询的，减轻下次递归时查询数量
$optionsTmp = $this->getTreeOptions3($list, $value['id']);//递归
if (!empty($optionsTmp)) { $options = array_merge($options, $optionsTmp);
}
}
} return $options;
}2、第二种是利用入栈、出栈的递归来计算，效率比上个好点，但是也挺慢的。流程是先反转数组，然后取出顶级数组入栈，开始while循环，先出栈一个查找其下有没有子节点，如果有子节点，则将此子节点也入栈，下次while循环就会查子节点的，依次类推：
function getTreeOptions2($list, $pid = 0)
{ $tree = []; if (!empty($list)) { //先将数组反转，因为后期出栈时会优先出最上面的
$list = array_reverse($list); //先取出顶级的来压入数组$stack中，并将在$list中的删除掉
$stack = []; foreach ($list as $key => $value) { if ($value['pid'] == $pid) { array_push($stack,$value); unset($list[$key]);
}
} while (count($stack)) { //先从栈中取出第一项
$info = array_pop($stack); //查询剩余的$list中pid与其id相等的，也就是查找其子节点
foreach ($list as $key => $child) { if ($child[pid] == $info['id']) { //如果有子节点则入栈，while循环中会继续查找子节点的下级
array_push($stack, $child); unset($list[$key]);
}
} //组装成下拉菜单格式
$tree[$info['id']] = $info['name'];
}
} return $tree;
}3、利用引用来处理，这个真的很巧妙，而且效率最高，可参照这里：
/**
* 先生成类似下面的形式的数据
* [
* 'id'=>1,
* 'pid'=>0,
* 'items'=>[
* 'id'=>2,
* 'pid'=>'1'
* 。。。
* ]
* ]*/function getTree($list, $pid = 0)
{ $tree = []; if (!empty($list)) { //先修改为以id为下标的列表
$newList = []; foreach ($list as $k => $v) { $newList[$v['id']] = $v;
} //然后开始组装成特殊格式
foreach ($newList as $value) { if ($pid == $value['pid']) {//先取出顶级
$tree[] = &$newList[$value['id']];
} elseif (isset($newList[$value['pid']])) {//再判定非顶级的pid是否存在，如果存在，则再pid所在的数组下面加入一个字段items，来将本身存进去
$newList[$value['pid']]['items'][] = &$newList[$value['id']];
}
}
} return $tree;
}然后再递归生成select下拉菜单所需要的，由于上方的特殊格式，导致递归起来非常快：
function formatTree($tree)
{ $options = []; if (!empty($tree)) { foreach ($tree as $key => $value) { $options[$value['id']] = $value['name']; if (isset($value['items'])) {//查询是否有子节点
$optionsTmp = $this->formatTree($value['items']); if (!empty($optionsTmp)) { $options = array_merge($options, $optionsTmp);
}
}
}
} return $options;
}以上三种，对于数据量小的来说，无所谓用哪种，但是对于数据量大的来说就非常明显了，用4000条地区数据测试结果效率对比：
第一种方法（递归）耗时：8.9441471099854左右
第二种方法（迭代）耗时：6.7250330448151左右
第三种方法（引用）耗时：0.028863906860352左右
我去，这差距，第三种方法真是逆天了。但是再次提醒，这只是一次性读取多的数据的时候，当数据量很小的时候，相差无几，不一定非要用最高效率的，还可以通过懒加载等其他方式来实现。
顺便封装个类，可以增加一些填充什么的。更多的细节可以查看下面的类：
1 <?php 2 /** 3 * parent_id类型树结构相关 4 * 没必要非要写成静态的方法，静态方法参数太多，所以用实例在构造函数中修改参数更合适 5 * 需要首先将所有数据取出，然后再用此方法重新规划数组，其它的边取边查询数据库的方法不推荐 6 * 经测试第一种方法要快很多，建议使用 7 * @author vishun <nadirvishun@gmail.com> 8 */ 9 10 class Tree 11 { 12 /** 13 * 图标 14 */ 15 public $icon = '└'; 16 /** 17 * 填充 18 */ 19 public $blank = ' '; 20 /** 21 * 默认ID字段名称 22 */ 23 public $idName = 'id'; 24 /** 25 * 默认PID字段名称 26 */ 27 public $pidName = 'pid'; 28 /** 29 * 默认名称字段名称 30 */ 31 public $titleName = 'name'; 32 /** 33 * 默认子元素字段名称 34 */ 35 public $childrenName = 'items'; 36 37 /** 38 * 构造函数，可覆盖默认字段值 39 * @param array $config 40 */ 41 function construct($config = []) 42 { 43 if (!empty($config)) { 44 foreach ($config as $name => $value) { 45 $this->$name = $value; 46 } 47 } 48 } 49 50 /** 51 * 生成下拉菜单可用树列表的方法 52 * 经测试4000条地区数据耗时0.02左右，比另外两种方法快超级多 53 * 流程是先通过引用方法来生成一种特殊树结构，再通过递归来解析这种特殊的结构 54 * @param array $list 55 * @param int $pid 56 * @param int $level 57 * @return array 58 */ 59 public function getTreeOptions($list, $pid = 0, $level = 0) 60 { 61 //先生成特殊规格的树 62 $tree = $this->getTree($list, $pid); 63 //再组装成select需要的形式 64 return $this->formatTree($tree, $level); 65 } 66 67 /** 68 * 通过递归来解析特殊的树结构来组装成下拉菜单所需要的样式 69 * @param array $tree 特殊规格的数组 70 * @param int $level 71 * @return array 72 */ 73 protected function formatTree($tree, $level = 0) 74 { 75 $options = []; 76 if (!empty($tree)) { 77 $blankStr = str_repeat($this->blank, $level) . $this->icon; 78 if ($level == 0) {//第一次无需有图标及空格 79 $blankStr = ''; 80 } 81 foreach ($tree as $key => $value) { 82 $options[$value[$this->idName]] = $blankStr . $value[$this->titleName]; 83 if (isset($value[$this->childrenName])) {//查询是否有子节点 84 $optionsTmp = $this->formatTree($value[$this->childrenName], $level + 1); 85 if (!empty($optionsTmp)) { 86 $options = array_merge($options, $optionsTmp); 87 } 88 } 89 } 90 } 91 return $options; 92 } 93 94 /** 95 * 生成类似下种格式的树结构 96 * 利用了引用&来实现，参照：http://blog.csdn.net/gxdvip/article/details/24434801 97 * [ 98 * 'id'=>1, 99 * 'pid'=>0,100 * 'items'=>[101 * 'id'=>2,102 * 'pid'=>'1'103 * 。。。104 * ]105 * ]106 * @param array $list107 * @param int $pid108 * @return array109 */110 protected function getTree($list, $pid = 0)111 {112 $tree = [];113 if (!empty($list)) {114 //先修改为以id为下标的列表115 $newList = [];116 foreach ($list as $k => $v) {117 $newList[$v[$this->idName]] = $v;118 }119 //然后开始组装成特殊格式120 foreach ($newList as $value) {121 if ($pid == $value[$this->pidName]) {122 $tree[] = &$newList[$value[$this->idName]];123 } elseif (isset($newList[$value[$this->pidName]])) {124 $newList[$value[$this->pidName]][$this->childrenName][] = &$newList[$value[$this->idName]];125 }126 }127 }128 return $tree;129 }130 131 /**132 * 第二种方法，利用出入栈迭代来实现133 * 经测试4000条地区数据耗时6.5s左右，比较慢134 * @param $list135 * @param int $pid136 * @param int $level137 * @return array138 */139 public function getTreeOptions2($list, $pid = 0, $level = 0)140 {141 $tree = [];142 if (!empty($list)) {143 144 //先将数组反转，因为后期出栈时会有限出最上面的145 $list = array_reverse($list);146 //先取出顶级的来压入数组$stack中，并将在$list中的删除掉147 $stack = [];148 foreach ($list as $key => $value) {149 if ($value[$this->pidName] == $pid) {150 array_push($stack, ['data' => $value, 'level' => $level]);//将层级记录下来，方便填充空格151 unset($list[$key]);152 }153 }154 while (count($stack)) {155 //先从栈中取出第一项156 $info = array_pop($stack);157 //查询剩余的$list中pid与其id相等的，也就是查找其子节点158 foreach ($list as $key => $child) {159 if ($child[$this->pidName] == $info['data'][$this->idName]) {160 //如果有子节点则入栈，while循环中会继续查找子节点的下级161 array_push($stack, ['data' => $child, 'level' => $info['level'] + 1]);162 unset($list[$key]);163 }164 }165 //组装成下拉菜单格式166 $blankStr = str_repeat($this->blank, $info['level']) . $this->icon;167 if ($info['level'] == 0) {//第一次无需有图标及空格168 $blankStr = '';169 }170 $tree[$info['data'][$this->idName]] = $blankStr . $info['data'][$this->titleName];171 }172 }173 return $tree;174 }175 176 /**177 * 第三种普通列表转为下拉菜单可用的树列表178 * 经测试4000条地区数据耗时8.7s左右，最慢179 * @param array $list 原数组180 * @param int $pid 起始pid181 * @param int $level 起始层级182 * @return array183 */184 public function getTreeOptions3($list, $pid = 0, $level = 0)185 {186 $options = [];187 if (!empty($list)) {188 $blankStr = str_repeat($this->blank, $level) . $this->icon;189 if ($level == 0) {//第一次无需有图标及空格190 $blankStr = '';191 }192 foreach ($list as $key => $value) {193 if ($value[$this->pidName] == $pid) {194 $options[$value[$this->idName]] = $blankStr . $value[$this->titleName];195 unset($list[$key]);//销毁已查询的，减轻下次递归时查询数量196 $optionsTmp = $this->getTreeOptions3($list, $value[$this->idName], $level + 1);//递归197 if (!empty($optionsTmp)) {198 $options = array_merge($options, $optionsTmp);199 }200 }201 }202 }203 return $options;204 }205 }View Code
以上记录下，如转载请标明来源地址
以上是无限极分类的三种方式（迭代、递归、引用）的详细内容。更多信息请关注PHP中文网其他相关文章！
热AI工具
Undresser.AI Undress
人工智能驱动的应用程序，用于创建逼真的裸体照片
AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。
Undress AI Tool
免费脱衣服图片
Clothoff.io
AI脱衣机
Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸！
热门文章
热工具
记事本++7.3.1
好用且免费的代码编辑器
SublimeText3汉化版
中文版，非常好用
禅工作室 13.0.1
功能强大的PHP集成开发环境
Dreamweaver CS6
视觉化网页开发工具
SublimeText3 Mac版
神级代码编辑软件(SublimeText3)
热门话题
C++ 函数的递归实现：递归深度有限制吗？
Apr 23, 2024 am 09:30 AM
C++函数的递归深度受到限制，超过该限制会导致栈溢出错误。限制值因系统和编译器而异，通常在1000到10000之间。解决方法包括：1.尾递归优化；2.尾调用；3.迭代实现。
C++ lambda 表达式是否支持递归？
Apr 17, 2024 pm 09:06 PM
是的，C++Lambda表达式可以通过使用std::function支持递归：使用std::function捕获Lambda表达式的引用。通过捕获的引用，Lambda表达式可以递归调用自身。
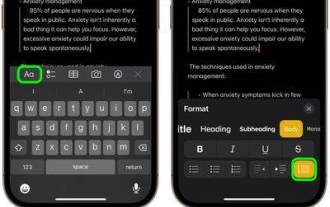如何在苹果笔记中使用块引号
Oct 12, 2023 pm 11:49 PM
在iOS17和macOSSonoma中，Apple为AppleNotes添加了新的格式选项，包括块引号和新的Monostyle样式。以下是使用它们的方法。借助AppleNotes中的其他格式选项，您现在可以在笔记中添加块引用。块引用格式可以轻松地使用文本左侧的引用栏直观地偏移部分的写作。只需点击/单击“Aa”格式按钮，然后在键入之前或当您在要转换为块引用的行上时选择块引用选项。该选项适用于所有文本类型、样式选项和列表，包括清单。在同一“格式”菜单中，您可以找到新的“单样式”选项。这是对先前“等宽
C++ 函数的递归实现：递归与非递归算法的比较分析？
Apr 22, 2024 pm 03:18 PM
递归算法通过函数自调用解决结构化的问题，优点是简洁易懂，缺点是效率较低且可能发生堆栈溢出；非递归算法通过显式管理堆栈数据结构避免递归，优点是效率更高且避免堆栈溢出，缺点是代码可能更复杂。选择递归或非递归取决于问题和实现的具体限制。
在Java中递归地计算子字符串出现的次数
Sep 17, 2023 pm 07:49 PM
给定两个字符串str_1和str_2。目标是使用递归过程计算字符串str1中子字符串str2的出现次数。递归函数是在其定义中调用自身的函数。如果str1是"Iknowthatyouknowthatiknow"，str2是"know"出现次数为-3让我们通过示例来理解。例如输入str1="TPisTPareTPamTP",str2="TP";输出Countofoccurrencesofasubstringrecursi
C++ 函数递归详解：递归在字符串处理中的应用
Apr 30, 2024 am 10:30 AM
递归函数是一种在字符串处理中反复调用自身来解决问题的技术。它需要一个终止条件以防止无限递归。递归在字符串反转和回文检查等操作中被广泛使用。
C++ 递归进阶：理解尾递归优化及其应用
Apr 30, 2024 am 10:45 AM
尾递归优化(TRO)可提高特定递归调用的效率。它将尾递归调用转换为跳转指令，并将上下文状态保存在寄存器中，而不是堆栈上，从而消除对堆栈的额外调用和返回操作，提高算法效率。利用TRO，我们可以针对尾递归函数（例如阶乘计算）进行优化，通过将tail递归调用替换为goto语句，编译器会将goto跳转移化为TRO，优化递归算法的执行。
C++ 函数返回引用类型有什么好处？
Apr 20, 2024 pm 09:12 PM
C++中的函数返回引用类型的好处包括：性能提升：引用传递避免了对象复制，从而节省了内存和时间。直接修改：调用方可以直接修改返回的引用对象，而无需重新赋值。代码简洁：引用传递简化了代码，无需额外的赋值操作。
