排序算法的稳定性及意义
冒泡排序
复杂度与稳定性
选择排序
插入排序
希尔排序
快速排序
常见排序算法效率比较
在待排序的序列中，存在具有相同关键字的记录，在排序后这些记录的相对次序保持不变，则排序算法是稳定的。
不稳定排序无法完成多个关键字的排序。例如整数排序，位数越高的数字优先级越高，从高位数到低位数一次排序。那么每一位的排序都需要稳定算法，否则无法得到正确的结果。
即，当要对多个关键词多次排序时，必须使用稳定算法

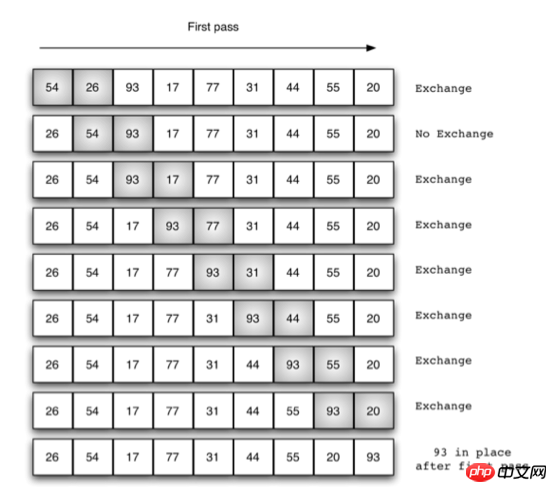
def bubble_sort(alist):
"""
冒泡排序
"""
if len(alist) <= 1:
return alist
for j in range(len(alist)-1,0,-1):
for i in range(j):
if alist[i] > alist[i+1]:
alist[i], alist[i+1] = alist[i+1], alist[i]
return alist最优时间复杂度：\(O(n)\) 遍历没有发现任何可以交换的元素，排序结束
最坏时间复杂度：\(O(n^2)\)
稳定性：稳定
选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。
插入排序通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

def insert_sort(alist):
"""
插入排序
"""
n = len(alist)
if n <= 1:
return alist
# 从第二个位置，即下表为1的元素开始向前插入
for i in range(1, n):
j = i
# 向前向前比较，如果小于前一个元素，交换两个元素
while alist[j] < alist[j-1] and j > 0:
alist[j], alist[j-1] = alist[j-1], alist[j]
j-=1
return alist复杂度与稳定性
最优时间复杂度：O(\(n\)) （升序排列，序列已经处于升序状态）
最坏时间复杂度：O(\(n^2\))
稳定性：稳定
希尔排序(Shell Sort)是插入排序的改进, 排序非稳定。希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
def shell_sort(alist): n = len(alist) gap = n//2 # gap 变化到0之前，插入算法之行的次数 while gap > 0: # 希尔排序， 与普通的插入算法的区别就是gap步长 for i in range(gap,n): j = i while alist[j] < alist[j-gap] and j > 0: alist[j], alist[j-gap] = alist[j-gap], alist[j] j-=gap gap = gap//2 return alist
复杂度与稳定性
最优时间复杂度：\(O(n^{1.3})\) （不要求本身有序）
最坏时间复杂度：\(O(n^2)\)
稳定性：不稳定
快速排序(Quicksort)，通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
步骤为：
从数列中挑出一个元素，称为"基准"(pivot)
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区(partition)操作。
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会结束，因为在每次的迭代(iteration)中，它至少会把一个元素摆到它最后的位置去。

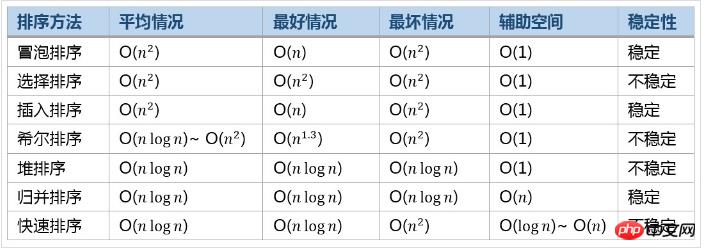
以上是分享Python常用的排序实例的详细内容。更多信息请关注PHP中文网其他相关文章！
