前端实现连连看小游戏实例代码
博主玩了这么久的连连看,居然是第一次发现,连连看最多只能有2个转弯。orz…
在网上搜索连连看的连线算法判断,并没有找到很全面的,经过自己摸索之后,画了下面的图(图有点丑……)
一. 2个物体在同一直线上,可以直接连通 (这个不需要解释啦)

二.2个物体在同一直线上,中间有障碍物,不能直接连通 (2个转弯)
【循环遍历黄线中的交点,比如A,B点,再判断蓝线有没有障碍物,若没有,则可以连通,若有,则继续循环查找新的A,B点】

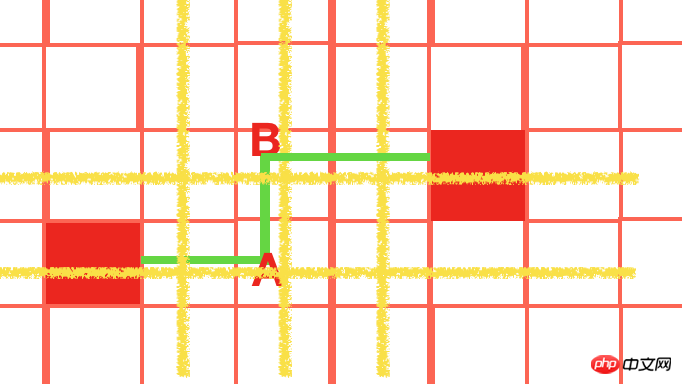
三. 2个对象不在同一直线上,一个转弯
【2个物体分别在所在位置进行x,y轴的延伸,如下图则交点为A,B。 只需判断2个交点到2个物体直接是否有障碍物,若没有,则可以连通】

四. 2个物体不在同一直线上,连线有2个转弯
【同二的原理,如下图,如果A,B 2个交点到物体均没有障碍物,则可以连通。其中A点的纵坐标和B相同】
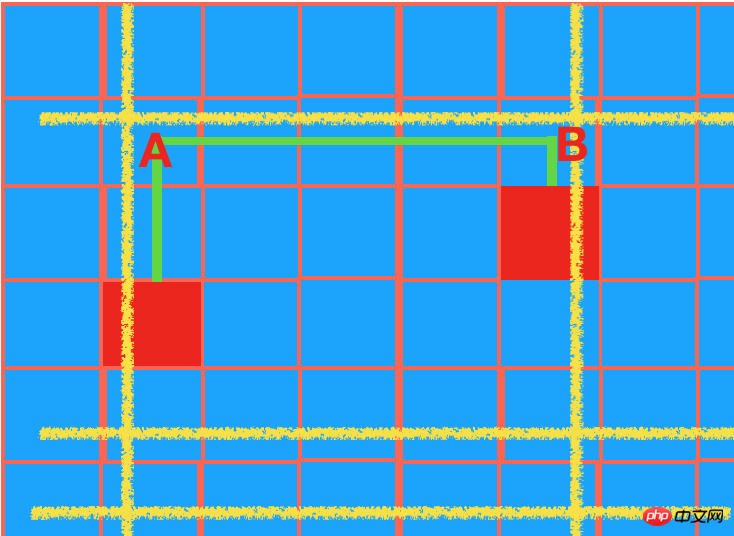
另外一种情况,A,B 为2个物体所在x轴与中间y轴的交点,A,B的x坐标必须相同,连线如下:
以上就是四种连线算法判断,画图只画x轴的,每一种按照同样的原理增加y轴即可。可覆盖所有连线判断~
说完连线判断的逻辑之后,写一下整体的游戏框架,游戏基本使用原生javascript,使用createjs游戏引擎进行开发。
代码思路:
1. 绘制游戏画图,确定为多少宫图,由于是在移动端的小游戏,根据最小屏幕尺寸(iphone4 320*480),确定为7*9的宫图。
1. 创建一个二维数组,如果某个坐标上有物体,则设为1,否则为0
2.判断该位置是否有物体,只需要判断对应的二维数组上值是否为1,若为1,则有物体,否则没有。
至于画线,消除相同物体,只要会连线逻辑,肯定就会自己绘制线条,消除物体了,所以本篇文章就只讲连线判断啦~
在判断能否连线的时候,肯定是从最简单的方法开始判断,如下:
同一直线能否直线连通--->如何一点被包围,则不通--->两点在一条直线上,不能直线连接但是可以连通---> 不在同一直线但是可以连通
getPath: function (p1, p2) {//开始搜索前对p1,p2排序,使p2尽可能的在p1的右下方。if (p1.x > p2.x) {var t = p1;
p1 = p2;
p2 = t;
}else if (p1.x == p2.x) {if (p1.y > p2.y) {var t = p1;
p1 = p2;
p2 = t;
}
}//2点在同一直线上,可以直线连通if (this.hasLine(p1, p2).status) {return true;
}//如果两点中任何一个点被全包围,则不通。else if (this.isWrap(p1, p2)) {return false;
}//两点在一条直线上,不能直线连接但是可以连通else if (this.LineLink(p1, p2)) {return true;
}//不在同一直线但是可以连通else if (this.curveLink(p1, p2)) {return true;
}
}


//判断同一条线能否连通,x轴相同或者y轴相同hasLine: function (p1, p2) {this.path = [];//同一点if (p1.x == p2.x && p1.y == p2.y) {return {
status: false};
}if (this.onlineY(p1, p2)) {var min = p1.y > p2.y ? p2.y : p1.y;
min = min + 1;var max = p1.y > p2.y ? p1.y : p2.y;for (min; min < max; min++) {var p = {x: p1.x, y: min};if (!this.isEmpty(p)) {
console.log('有障碍物p点………………');
console.log(p);this.path = [];break;
}this.path.push(p);
}if (min == max) {return {
status: true,
data: this.path,
dir: 'y' //y轴 };
}this.path = [];return {
status: false};
}else if (this.onlineX(p1, p2)) {var j = p1.x > p2.x ? p2.x : p1.x;
j = j + 1;var max = p1.x > p2.x ? p1.x : p2.x;for (j; j < max; j++) {var p = {x: j, y: p1.y};if (!this.isEmpty(p)) {
console.log('有障碍物p点………………');
console.log(p);this.path = [];break;
}this.path.push(p);
}if (j == max) {return {
status: true,
data: this.path,
dir: 'x' //x轴 };
}this.path = [];return {
status: false};
}return {
status: false};//2点是否有其中一点被全包围,若有,则返回trueisWrap: function (p1, p2) {//有一点为空,则条件不成立if (!this.isEmpty({x: p1.x, y: p1.y + 1}) && !this.isEmpty({
x: p1.x,
y: p1.y - 1}) && !this.isEmpty({
x: p1.x - 1,
y: p1.y
}) && !this.isEmpty({x: p1.x + 1, y: p1.y})) {return true;
}if (!this.isEmpty({x: p2.x, y: p2.y + 1}) && !this.isEmpty({
x: p2.x,
y: p2.y - 1}) && !this.isEmpty({
x: p2.x - 1,
y: p2.y
}) && !this.isEmpty({x: p2.x + 1, y: p2.y})) {return true;
}return false;
} //两点在一条直线上,不能直线连接但是可以连通LineLink: function (p1, p2) {var pt0, pt1, pt2, pt3;//如果都在x轴,则自左至右扫描可能的路径,//每次构造4个顶点pt0, pt1, pt2, pt3,然后看他们两两之间是否连通if (this.onlineX(p1, p2)) {for (var i = 0; i < this.H; i++) {if (i == p1.y) {continue;
}
pt0 = p1;
pt1 = {x: p1.x, y: i};
pt2 = {x: p2.x, y: i};
pt3 = p2;//如果顶点不为空,则该路不通。if (!this.isEmpty(pt1) || !this.isEmpty(pt2)) {continue;
}if (this.hasLine(pt0, pt1).status && this.hasLine(pt1, pt2).status && this.hasLine(pt2, pt3).status) {this.drawLine(2, [pt0, pt3, pt1, pt2]);return [pt0, pt1, pt2, pt3];
}
}
}//如果都在y轴,则自上至下扫描可能的路径,//每次构造4个顶点pt0, pt1, pt2, pt3,然后看他们两两之间是否连通if (this.onlineY(p1, p2)) {for (var j = 0; j < this.W; j++) {if (j == p1.x) {continue;
}
pt0 = p1;
pt1 = {x: j, y: p1.y};
pt2 = {x: j, y: p2.y};
pt3 = p2;//如果顶点不为空,则该路不通。if (!this.isEmpty(pt1) || !this.isEmpty(pt2)) {continue;
}if (this.hasLine(pt0, pt1).status && this.hasLine(pt1, pt2).status && this.hasLine(pt2, pt3).status) {this.drawLine(2, [pt0, pt3, pt1, pt2]);return [pt0, pt1, pt2, pt3];
}
}
}
}, //两点不在一条直线上,看是否可通curveLink: function (p1, p2) {var pt0, pt1, pt2, pt3;//特殊情况,先判断是否是一个转弯var spec1 = {x: p1.x, y: p2.y},
spec2 = {x: p2.x, y: p1.y};if (this.isEmpty(spec1)) {if (this.hasLine(p1, spec1).status && this.hasLine(p2, spec1).status) {
console.log('1个转弯');this.drawLine(1, [p1, p2, spec1]);return [p1, p2, spec1];
}
}if (this.isEmpty(spec2)) {if (this.hasLine(p1, spec2).status && this.hasLine(p2, spec2).status) {
console.log('1个转弯');// console.table([pt0, spec2, pt3]);this.drawLine(1, [p1, p2, spec2]);return [p1, spec2, p2];
}
}//先纵向扫描可能的路径//同样,每次构造4个顶点,看是否可通for (var k = 0; k <= this.H; k++) {
pt0 = p1;
pt1 = {x: p1.x, y: k};
pt2 = {x: p2.x, y: k};
pt3 = p2;//2个交点都为空if (this.isEmpty(pt1) && this.isEmpty(pt2)) {//2个转弯if (this.hasLine(pt0, pt1).status && this.hasLine(pt1, pt2).status && this.hasLine(pt2, pt3).status) {
console.log('2个转弯');this.drawLine(2, [pt0, pt3, pt1, pt2]);return [pt0, pt3, pt1, pt2];
}
}
}//横向扫描所有可能的路径for (var k = 0; k <= this.W; k++) {
pt0 = p1;
pt1 = {x: k, y: p1.y};
pt2 = {x: k, y: p2.y};
pt3 = p2;//2个交点都为空if (this.isEmpty(pt1) && this.isEmpty(pt2)) {//2个转弯if (this.hasLine(pt0, pt1).status && this.hasLine(pt1, pt2).status && this.hasLine(pt2, pt3).status) {
console.log('2个转弯');this.drawLine(2, [pt0, pt3, pt1, pt2]);return [pt0, pt3, pt1, pt2];
}
}
}return false;
}
以上是前端实现连连看小游戏实例代码的详细内容。更多信息请关注PHP中文网其他相关文章!

热AI工具

Undresser.AI Undress
人工智能驱动的应用程序,用于创建逼真的裸体照片

AI Clothes Remover
用于从照片中去除衣服的在线人工智能工具。

Undress AI Tool
免费脱衣服图片

Clothoff.io
AI脱衣机

Video Face Swap
使用我们完全免费的人工智能换脸工具轻松在任何视频中换脸!

热门文章

热工具

记事本++7.3.1
好用且免费的代码编辑器

SublimeText3汉化版
中文版,非常好用

禅工作室 13.0.1
功能强大的PHP集成开发环境

Dreamweaver CS6
视觉化网页开发工具

SublimeText3 Mac版
神级代码编辑软件(SublimeText3)
 华为手机如何实现双微信登录?
Mar 24, 2024 am 11:27 AM
华为手机如何实现双微信登录?
Mar 24, 2024 am 11:27 AM
华为手机如何实现双微信登录?随着社交媒体的兴起,微信已经成为人们日常生活中不可或缺的沟通工具之一。然而,许多人可能会遇到一个问题:在同一部手机上同时登录多个微信账号。对于华为手机用户来说,实现双微信登录并不困难,本文将介绍华为手机如何实现双微信登录的方法。首先,华为手机自带的EMUI系统提供了一个很便利的功能——应用双开。通过应用双开功能,用户可以在手机上同
 PHP编程指南:实现斐波那契数列的方法
Mar 20, 2024 pm 04:54 PM
PHP编程指南:实现斐波那契数列的方法
Mar 20, 2024 pm 04:54 PM
编程语言PHP是一种用于Web开发的强大工具,能够支持多种不同的编程逻辑和算法。其中,实现斐波那契数列是一个常见且经典的编程问题。在这篇文章中,将介绍如何使用PHP编程语言来实现斐波那契数列的方法,并附上具体的代码示例。斐波那契数列是一个数学上的序列,其定义如下:数列的第一个和第二个元素为1,从第三个元素开始,每个元素的值等于前两个元素的和。数列的前几个元
 如何在华为手机上实现微信分身功能
Mar 24, 2024 pm 06:03 PM
如何在华为手机上实现微信分身功能
Mar 24, 2024 pm 06:03 PM
如何在华为手机上实现微信分身功能随着社交软件的普及和人们对隐私安全的日益重视,微信分身功能逐渐成为人们关注的焦点。微信分身功能可以帮助用户在同一台手机上同时登录多个微信账号,方便管理和使用。在华为手机上实现微信分身功能并不困难,只需要按照以下步骤操作即可。第一步:确保手机系统版本和微信版本符合要求首先,确保你的华为手机系统版本已更新到最新版本,以及微信App
 PHP与Vue:完美搭档的前端开发利器
Mar 16, 2024 pm 12:09 PM
PHP与Vue:完美搭档的前端开发利器
Mar 16, 2024 pm 12:09 PM
PHP与Vue:完美搭档的前端开发利器在当今互联网高速发展的时代,前端开发变得愈发重要。随着用户对网站和应用的体验要求越来越高,前端开发人员需要使用更加高效和灵活的工具来创建响应式和交互式的界面。PHP和Vue.js作为前端开发领域的两个重要技术,搭配起来可以称得上是完美的利器。本文将探讨PHP和Vue的结合,以及详细的代码示例,帮助读者更好地理解和应用这两
 掌握Golang如何实现游戏开发的可能性
Mar 16, 2024 pm 12:57 PM
掌握Golang如何实现游戏开发的可能性
Mar 16, 2024 pm 12:57 PM
在当今的软件开发领域中,Golang(Go语言)作为一种高效、简洁、并发性强的编程语言,越来越受到开发者的青睐。其丰富的标准库和高效的并发特性使它成为游戏开发领域的一个备受关注的选择。本文将探讨如何利用Golang来实现游戏开发,并通过具体的代码示例来展示其强大的可能性。1.Golang在游戏开发中的优势作为一种静态类型语言,Golang在构建大型游戏系统
 如何在Golang中实现精确除法运算
Feb 20, 2024 pm 10:51 PM
如何在Golang中实现精确除法运算
Feb 20, 2024 pm 10:51 PM
在Golang中实现精确除法运算是一个常见的需求,特别是在涉及金融计算或其它需要高精度计算的场景中。Golang的内置的除法运算符“/”是针对浮点数计算的,并且有时会出现精度丢失的问题。为了解决这个问题,我们可以借助第三方库或自定义函数来实现精确除法运算。一种常见的方法是使用math/big包中的Rat类型,它提供了分数的表示形式,可以用来实现精确的除法运算
 PHP游戏需求实现指南
Mar 11, 2024 am 08:45 AM
PHP游戏需求实现指南
Mar 11, 2024 am 08:45 AM
PHP游戏需求实现指南随着互联网的普及和发展,网页游戏的市场也越来越火爆。许多开发者希望利用PHP语言来开发自己的网页游戏,而实现游戏需求是其中一个关键步骤。本文将介绍如何利用PHP语言来实现常见的游戏需求,并提供具体的代码示例。1.创建游戏角色在网页游戏中,游戏角色是非常重要的元素。我们需要定义游戏角色的属性,比如姓名、等级、经验值等,并提供方法来操作这些
 前端面试官常问的问题
Mar 19, 2024 pm 02:24 PM
前端面试官常问的问题
Mar 19, 2024 pm 02:24 PM
在前端开发面试中,常见问题涵盖广泛,包括HTML/CSS基础、JavaScript基础、框架和库、项目经验、算法和数据结构、性能优化、跨域请求、前端工程化、设计模式以及新技术和趋势。面试官的问题旨在评估候选人的技术技能、项目经验以及对行业趋势的理解。因此,应试者应充分准备这些方面,以展现自己的能力和专业知识。






